1P 2021 vår K06 LØSNING: Forskjell mellom sideversjoner
| Linje 250: | Linje 250: | ||
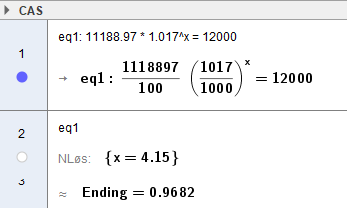
===b)=== | ===b)=== | ||
[[File:231021-01.png]] | |||
Den vil tidligst passere 12 000 kr. i august 2025. | |||
==Oppgave 7== | ==Oppgave 7== | ||
Sideversjonen fra 23. okt. 2021 kl. 11:03
Eksamen 26.05.2021 MAT1011 Matematikk 1P. Kunnskapsløftet.
Diskusjon av oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL EN
Oppgave 1
a)
Bruker Pytagoras og finner at avstanden AB er : $AB = \sqrt{300^2+400^2} = 500$ meter.
b)
$\frac{700-500}{500} = \frac 25 = 40$%. Sykkelturen er 40% lengre.
c)
Målestokk:
$\frac{4,0 cm}{0,8km} = \frac{4}{80000}= \frac{1}{20000}$
Målestokken er 1:20 000 som betyr at 1cm på kartet er 20 000 cm i virkeligheten, altså tilsvarer 1 cm på kartet 200 meter i virkeligheten.
Oppgave 2
$\frac{x}{80} = \frac{1200}{100}$
$ x = 12 \cdot 80 = 960$
Varen koster 960 kr, om den følger indeksen.
Oppgave 3
a)
Det koster 12 000 kroner.
Vi ser at to personer må betale 6000 kroner hver, eller at 4 personer betaler 3000 hver, osv.
b)
$x \cdot y = k$
Produktet av to omvendt proporsjonale størrelser er konstant. Nå x blir større, blir y mindre og motsatt. I dette eksempelet er k= 12 000 kr. I praksis betyr det at det blir billigere for den enkelte jo flere som er med på hytteturen.
c)
$y = \frac{12000}{x}$ Der y er prisen den enkelte betaler, og x er antall betalende personer.
Oppgave 4
Volum av boks: $V \approx 3 \cdot 25 \cdot 10 = 750$
Volumet av boksen er ca. 7,5 dl
Volumet av kaffe: $\frac{250}{35} = \frac{50}{7} = 7 + \frac 17$dl
Siden en syvendedel er mindre enn 0,5 får kaffen plass i boksen.
Oppgave 5
a)
I dette tilfelle er $x = \frac{40km/t}{10} = 4 $
Bremselengde ved 40 km/t =$ \frac{4^2}{2} = \frac{16}{2} = 8 $ m.
b)
Når farten øker til 80 km/t blir x = 8
Bruker samme formel og får $ \frac{8^2}{2} = \frac {64}{2} = 32$ som er fire ganger mere enn 8.
c)
På sommerføre ville en bil med fart 60 km/t hatt en bremselengde på 18 meter.
$\frac{72-18}{18} = \frac{54}{18} = 3$
Økningen i bremselengde er på 300%
Oppgave 6
a)
| Fornøyd | Ikke Fornøyd | Sum | |
| VG 1 | $48$ | $72$ | $120$ |
| VG 3 | $90$ | $60$ | $150$ |
| Sum | $138$ | $132$ | $270$ |
b)
Tilfeldig elev fornøyd. $P(F) = \frac{130}{270} =0,5$
c)
VG 3 gitt fornøyd: $P(vg3 | fornøyd) = \frac{90}{138} \approx 0,65$, eller 65%.
Oppgave 7
a)
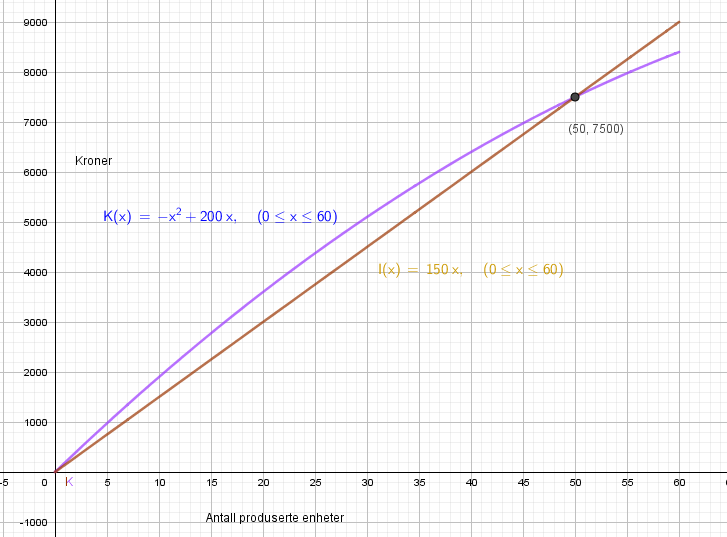
Vi sette x verdiene inn i uttrykket for K og får følgende tabell:
b)
c)
Fra figuren i b ser man at man må produsere 51 eller flere enheter før man får et overskudd.
DEL TO
Oppgave 1
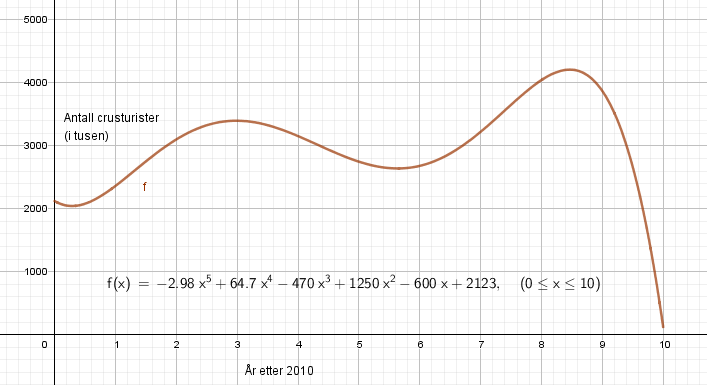
a)
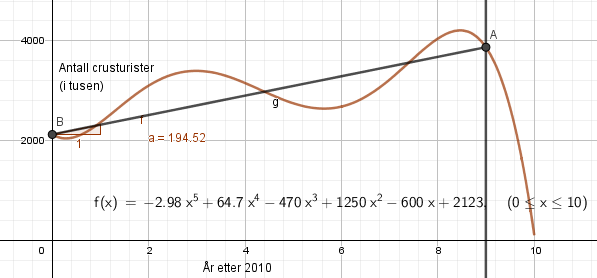
b)
Stigningstallet er 194,5. Det betyr at antall cruiseturister i perioden 2010-2019 økte i gjennomsnitt med ca. 194 500 per år.
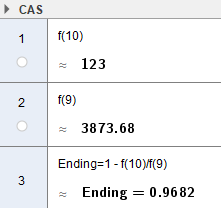
c)
Nedgangen var på nesten 97%.
Oppgave 2
a)
Når noe endrer seg lineært kan det skrives på formen y = ax + b.
Vi ser at på 5 år har innbyggertallet økt med 200. Det er en økning i snitt på 40 per år. Dersom vi lar x symboliserer år etter 2015 får vi
f(x) = 40x + 4600
Det som står under flekken er altså 40x.
b)
$f(15) = 40 \cdot 15 + 4600 = 5200$
Dersom modellen er god vil det være ca. 5200 innbyggere i bydelen i 2030.
Oppgave 3
Dersom han trekker uten tilbakelegging:
P(to av samme farge:) = P(to hvite) + P( to røde) =$\frac{6}{16} \cdot \frac{5}{15} + \frac{10}{16} \cdot \frac{9}{15} = \frac{24}{48} =0,5 $ = 50%
Vel dersom det er 50% sannsynlig at man trekker to drops med lik farge, må resten av mulighetene være ulik farge, altså 50% for det også.
Trekning med tilbakeligging:
P(to av samme farge:) = P(to hvite) + P( to røde) =$\frac{6}{16} \cdot \frac{6}{16} + \frac{10}{16} \cdot \frac{10}{16} = \frac{36+100}{256} =0,53 $ = 53%
Med tilbakelegging er ikke sannsynligheten for to like farger den samme som for to ulike farger. Detter er en svakhet med oppgaven og trekningsmetode burde vært presisert.
Oppgave 4
a)
En tomme = 2,54 cm
En lengde på 12,2 cm er da $\frac{12,2}{2,54} = 4,8$
Diagonalen er 4,8 tommer.
b)
Dersom forholdet er 16:9 mellom høyde og bredde, finner vi diagonalen ved Pytagoras, den blir 18,4 når forholdet mellom sidene er 16:9.
Vi vet at diagonalen er 12,2 cm og kan sette opp følgende forhold for å finne bredde og høyde:
$\frac{12,2}{18,4} = \frac{bredde}{9} \Rightarrow Bredde = 6 cm $
For å finne mobilens høyde bruker vi samme tankegang;
$\frac{12,2}{18,4} = \frac{høyde}{16} \Rightarrow Høyde = 10,6 cm $
c)
$\frac{(6,1)^2}{(4,8)^2} = \frac{37,21}{23,04}= 1,615$
Den nye telefonen har et areale som er 61,5% større enn den hun har nå.
Oppgave 5
a)
Rullen har form som en sylinder med radius 10 cm og høyde 80 cm. Vi må huske å trekke fra fra "sylinderen" som dannes av hullet i midten. $V = \pi r^2h $ som gir oss: $V_{papir} = \pi \cdot 10^2 \cdot 80 - \pi \cdot 0,7^2 \cdot 80 = 80 \pi(100 - 0,49) = 25,010 $. Vi har regnet i cm hele veien så $25010 cm^3 = 25,01dm^3$
b)
Når vi ruller ut papiret tenker vi at det har form som et prisme (boks) med en veldig liten høyde som tilsvarer tykkelsen på papiret.
$V = l \cdot b \cdot h \Rightarrow h = \frac{V}{l \cdot b} = \frac{25dm^3}{2500dm \cdot 8 dm} =0,00125 $ dm, som er 0,125 mm tykt.
c)
Papiret på rullen har en flate på $A = l \cdot b = 250 m \cdot 0,8 m = 200 m^2$
Da blir massen av papir $200m^2 \cdot 60 g/m^2 = 12000g = 12 kg$
Oppgave 6
a)
b)
Den vil tidligst passere 12 000 kr. i august 2025.