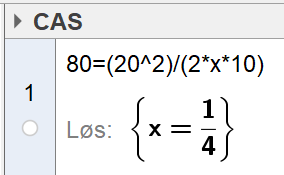1P 2021 vår LK20 LØSNING: Forskjell mellom sideversjoner
| Linje 175: | Linje 175: | ||
==Oppgave 16== | ==Oppgave 16== | ||
Bruker Excel for å sammenligne resultatene for gutter og jenter i ulike årsklasser. | |||
[[File: 3-16a.png]] | |||
Jeg ser at jentene i alle årsklasser bruker med tid enn guttene i samme årsklasse på 200 m løp. Jentene brukte omtrent 200-300 ms mer enn guttene, som tilsvarer at de brukte mer enn 10% mer tid enn guttene. Forskjellen var ganske like for årsklassene 15-17 år, men for årsklassen 18 år brukte jentene 13,5% mer tid enn guttene. | |||
Sideversjonen fra 28. jun. 2021 kl. 06:48
Eksamen 1P vår 2021 LK20 Fagfornyelsen
Diskusjon av oppgaven på matteprat
Oppgavetype 1
I oppgavetype 1 skal du bare oppgi svaret, uten begrunnelse. Vi gir allikevel en liten begrunnelse her, for å forstå hvordan vi har kommet frem til svaret.
Oppgave 1
Svar: 100 kroner.
Begrunnelse: Her er det mange måter å tenke på, men for eksempel: 22 kroner for 220 mL cappuccino gir 10 kroner for 100 mL cappuccino. I 1 liter er det 1000 mL. Hvis 100 mL cappuccino koster 10 kroner, vil da 1 liter (1000 mL) koste 100 kroner.
Oppgave 2
Svar: 11610 kroner
Begrunnelse: regner ut $25000\cdot 0,88^6$ på kalkulator eller CAS. 25000 kr er startverdien, 0,88 er vekstfaktoren ved 12% nedgang, og 6 er antall år.
Oppgave 3
Svar: 0,25
Begrunnelse: bruker CAS, og fyller inn verdien på de variablene jeg får opplyst i teksten. Jeg kaller $\mu$ for x, og bruker "løs" i CAS. Husk å skrive inn svaret som desimaltall, og ikke som brøk.
Oppgave 4
Svar: Midtre Gauldal
Begrunnelse: i denne oppgaven må du se nøye på verdiene på y-aksen. Det er fristende å svare Strand, hvor det ser ut som en stor økning, men da har man ikke sett ordentlig på y-aksen. I Strand øker aldri antall felte elger med mer enn 3 på ett år. I Skaum øker aldri antallet felte elger med mer enn ca. 25 elg per år. I Stjørdal øker ikke antallet med mer enn ca. 50 elg per år. I Midtre Gauldal har vi en økning på ca. 90 felte elg fra 2015 til 2016, dette er den største økningen.
Oppgave 5
Svar: 280 km
Begrunnelse: I Firma A er prisen 1200 kr uansett hvor langt Ester kjører. I Firma B er startprisen 500 kr, så øker deretter prisen med 200 kr for 80 km (du ser det f.eks. fra 40 km til 120 km, da har prisen gått fra 600 kr til 800 kr). Bildet stopper på 200 km og 1000 kr for Firma B. For at prisen skal bli lik Firma A, 1200 kr, må Ester kjøret 280 km med Firma B.
Oppgave 6
Svar: 250 kroner
Begrunnelse: prisen for å leie seilbåten alene er $5\cdot 700\,kr = 3500\,kr$. Prisen per person når 14 personer deler på prisen er $\frac{3500\,kr}{14}=250\,kr$
Oppgave 7
Svar: 79 %
Begrunnelse: Vi skal ha prosentandelen som bruker nettet til skolearbeid/lekser minst én gang hver uke, så du må legge sammen prosentandelen som bruker nettet til skolearbeid/lekser hver dag og hver uke. 35 % + 44 % = 79 %.
Oppgave 8
Svar: 1400 døgn
Begrunnelse: deler strekning på fart, for å finne tid. $\frac{1,4\cdot 10^9\,km}{1,0\cdot 10^6 \,km/døgn}=1400\,døgn$
Oppgavetype 2
I oppgavetype 2 skal du vise utregninger, forklare fremgangsmåter du har brukt, og begrunne resultater.
Oppgave 9
a)
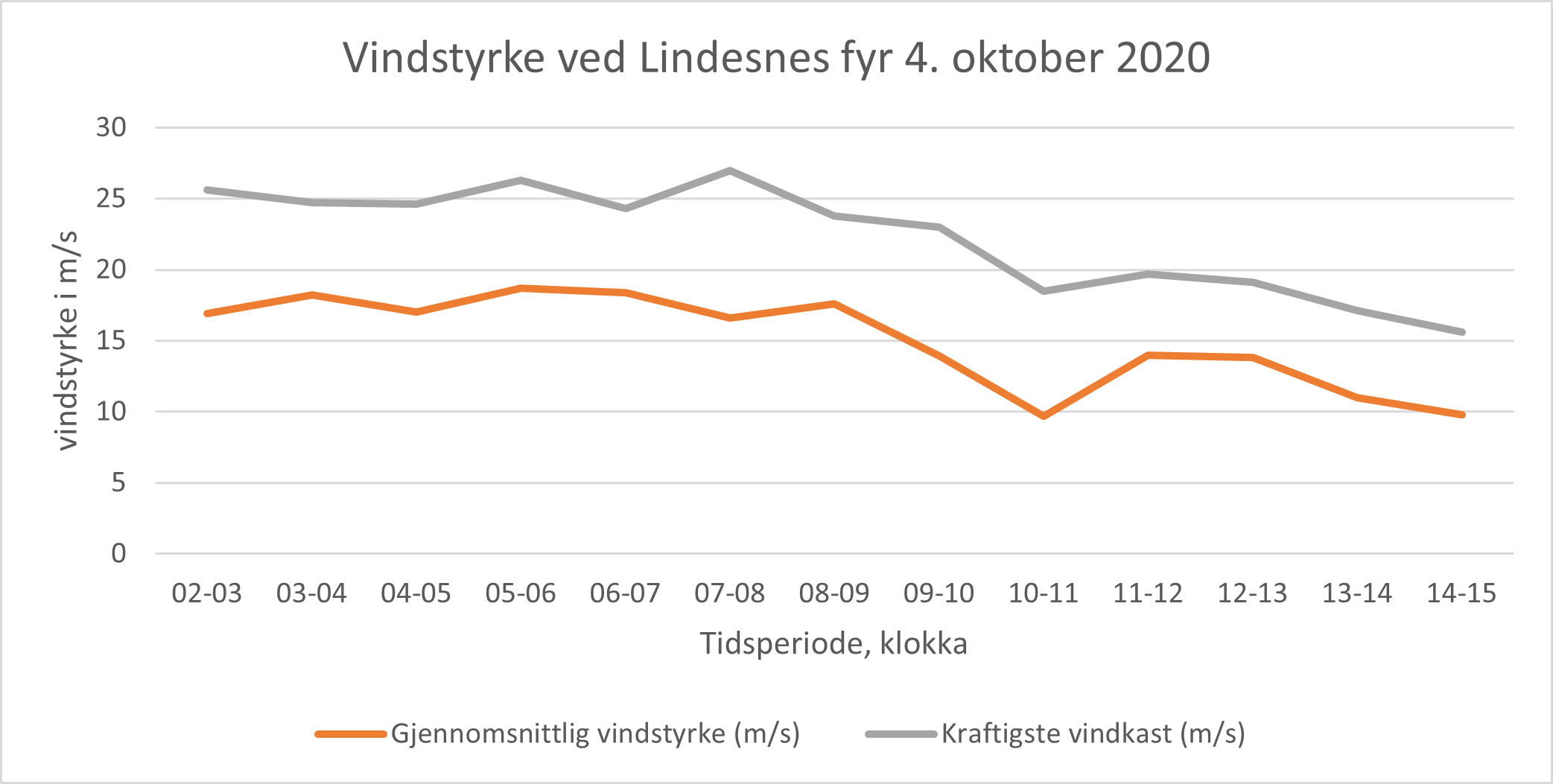
Lager et linjediagram i Excel. Ha med nødvendige aksetitler, tittel på diagrammet og forklaringstekst til linjene.
b)
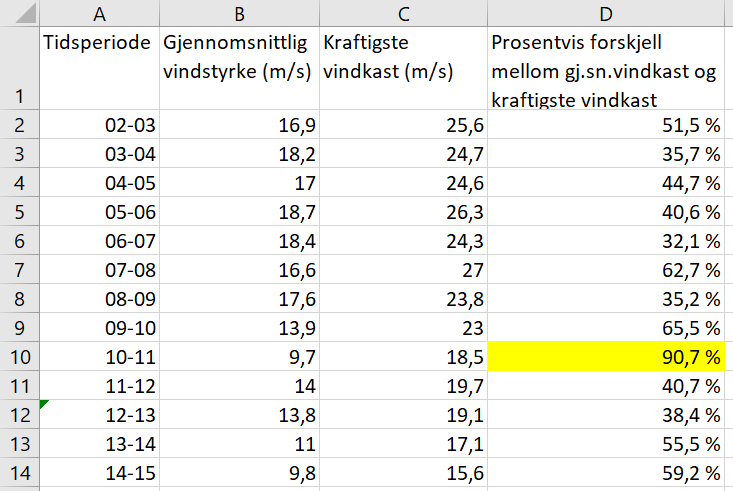
Bruker Excel til å beregne størst prosentvis forskjell mellom gjennomsnittlig vindstyrke og kraftigste vindkast i disse timene, og finner at den største forskjellen er i tidsperioden kl. 10-11.
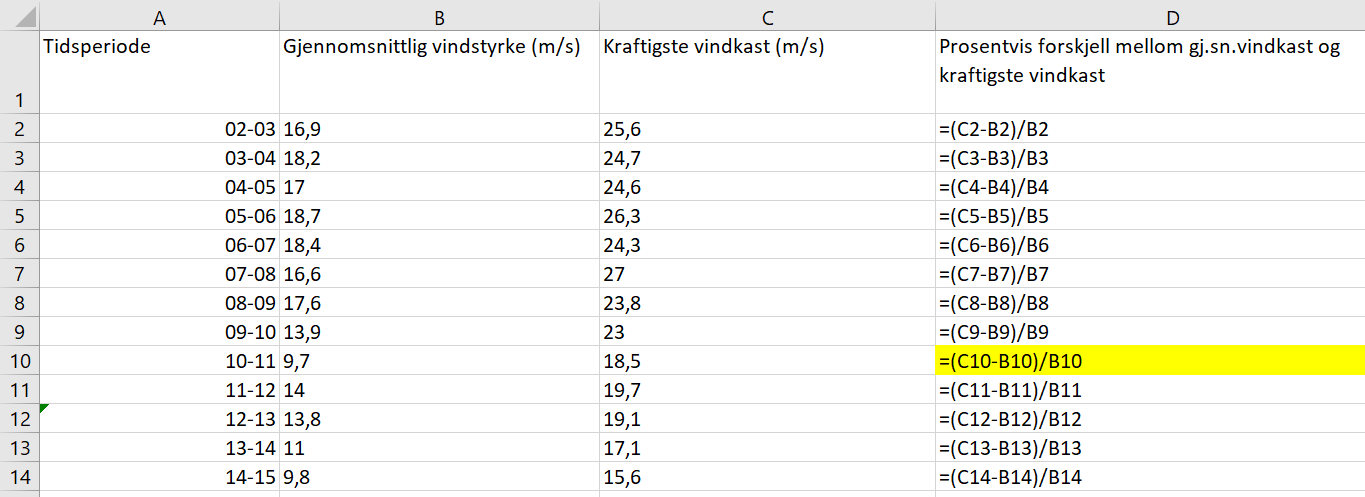
Skjermbilde fra Excel:
Med formler:
c)
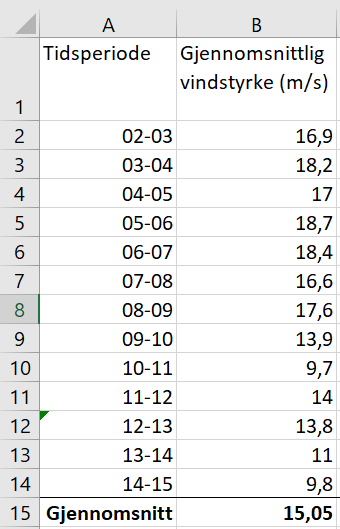
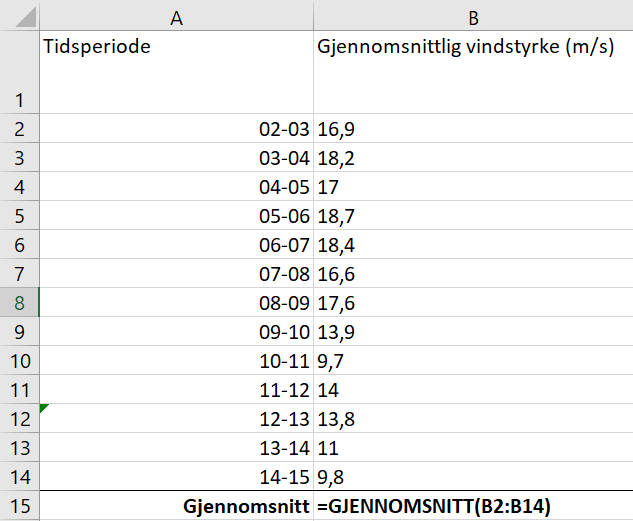
Bruker Excel til å beregne gjennomsnittet av vindstyrken i perioden kl.02 til 15 den 4. oktober.
Med formel:
Gjennomsnittlig vindstyrke var 15,05 m/s fra kl.02 til kl.15 den 4. oktober. Gjennomsnittlig vindstyrke for hele døgnet var 11,7 m/s. Det vil si at det i gjennomsnitt var lavere vindstyrke resten av døgnet, enn mellom kl. 02 og kl. 15.
Oppgave 10
a)
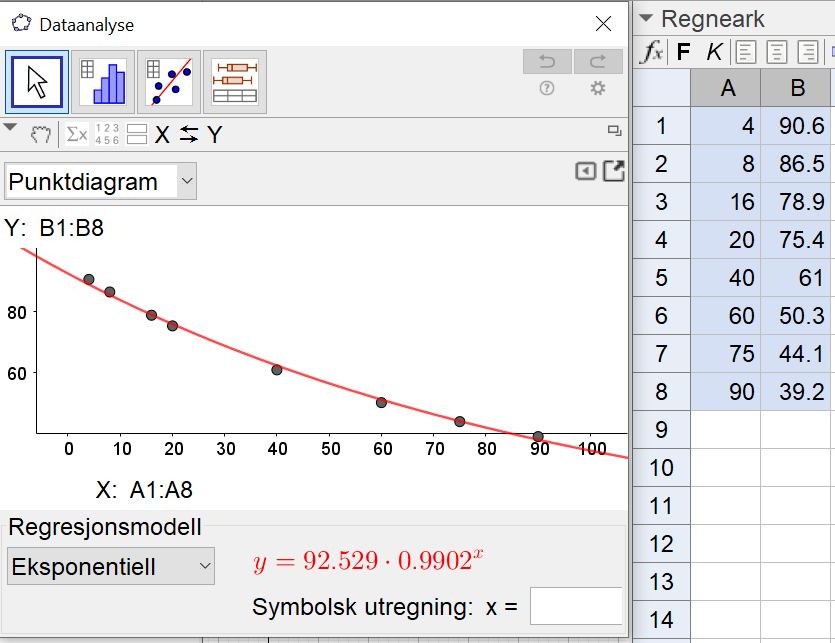
Bruker regresjonsanalyse i Geogebra. Velger eksponentiell modell.
Modellen som viser temperaturen i geléen x minutter etter at den ble satt til avkjøling er $T(x)=92,5 \cdot 0,99^x$
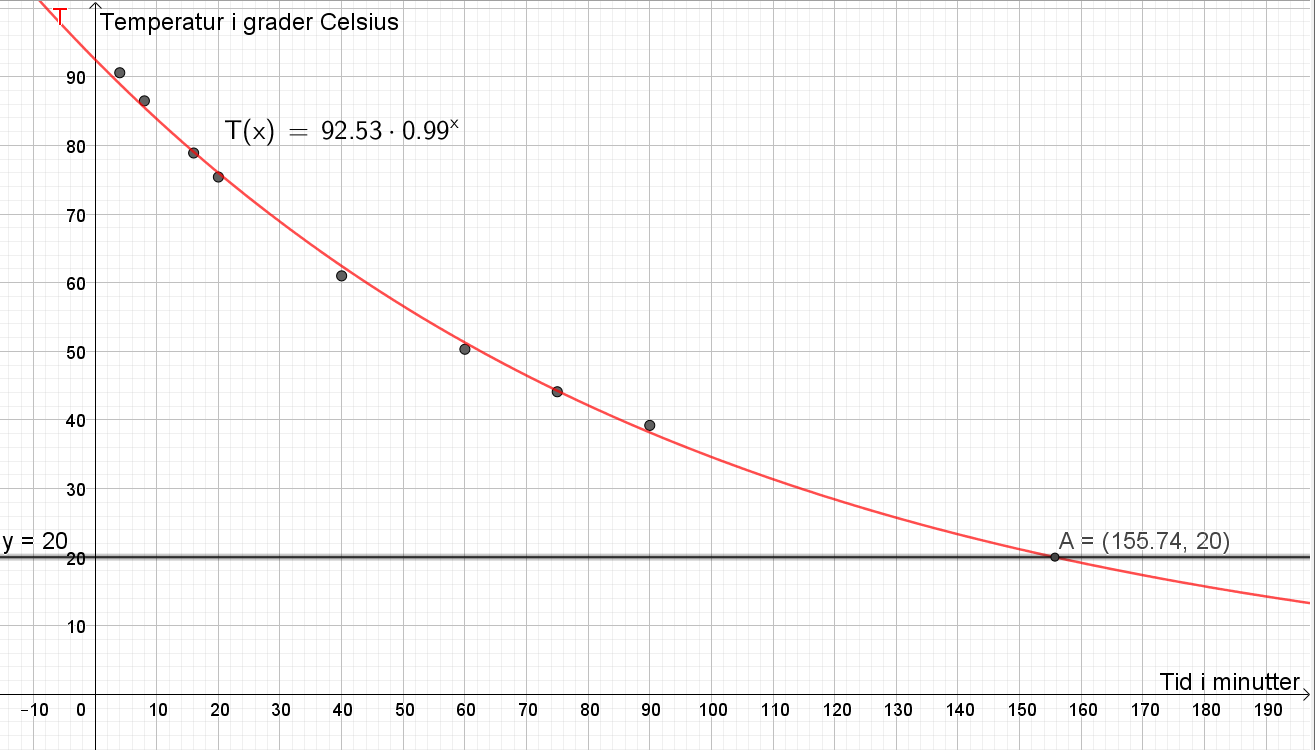
b)
Geléen ble satt til avkjøling i et rom der temperaturen var 20 grader Celsius. Det vil si at geléen ikke vil bli kaldere enn romtemperaturen, 20 grader. Jeg kopierer modellen til grafikkfeltet i Geogebra, og tegner linja y=20, og finner skjæringspunktet med grafen til T. Se punkt A=(155.7 , 20). Etter omtrent 155 minutter, har geléen en temperatur på 20 grader.
Gyldighetsområdet til modellen er fra 0 til 155 minutter, altså for $x \in [0,155]$.
Oppgave 11
a)
Jeg mener det er graf 2 som er grafen til $R$. I starten er det få som vet om ryktet, og spredningen går litt sakte til å begynne med. Etter hvert som flere blir kjent med ryktet, øker spredningen av ryktet raskere. Ryktet sprer seg raskest når halvparten av øyboerne vet om det. På slutten kjenner de fleste til ryktet, og ryktet sprer seg derfor saktere til alle kjenner til ryktet. Når alle kjenner ryktet, flater grafen ut. Dette passer med en sigmoid funksjon.
b)
Graf 1 er lineær. En lineær funksjon har et konstant stigningstall. Det er lite trolig at ryktet vil spre seg med like mange personer per tidsenhet.
Graf 3 er eksponentiell. Det er ikke en realistisk modell at ryktet sprer seg raskere og raskere når over halvparten av øyboerne kjenner ryktet.
Oppgave 12
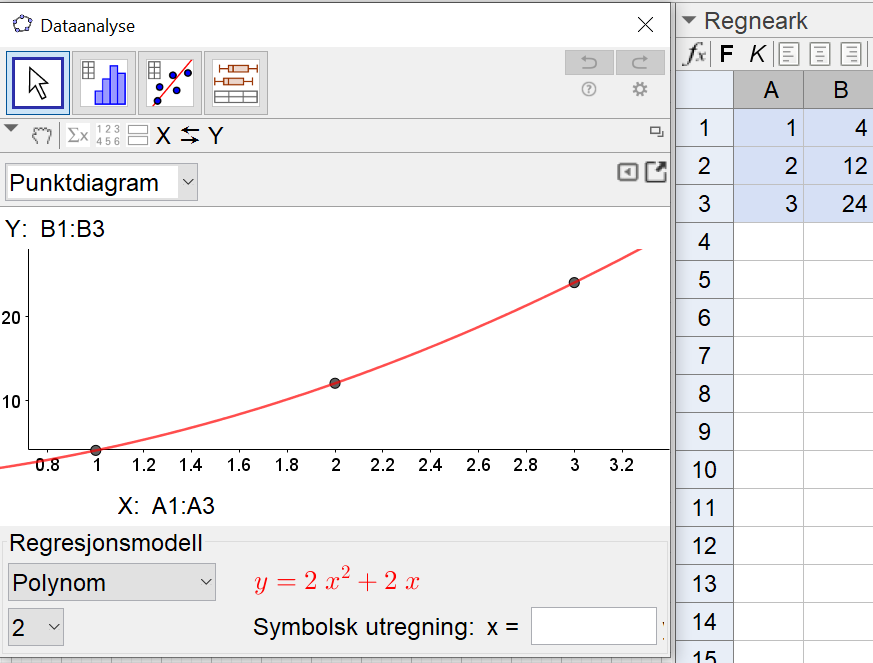
Bruker Regresjonsanalyse i Geogebra til å finne en funksjon a(n) for antall fyrstikker i figur n. Jeg ser at polynomregresjon passer, og får $a(n)=2n^2+2n$
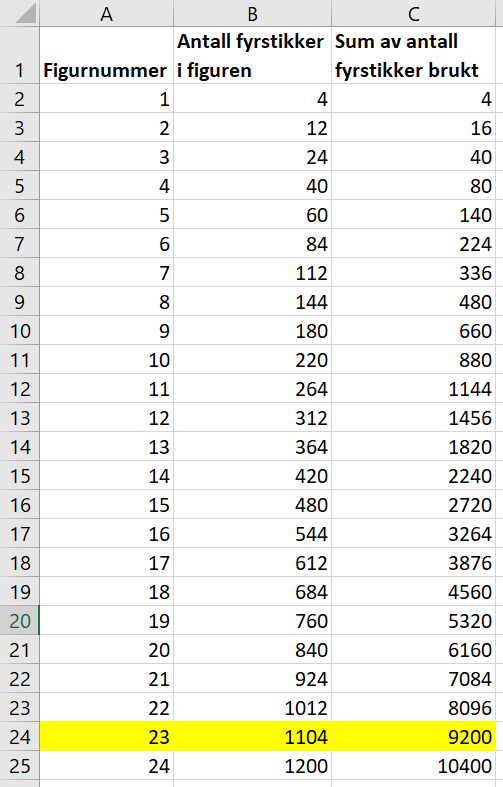
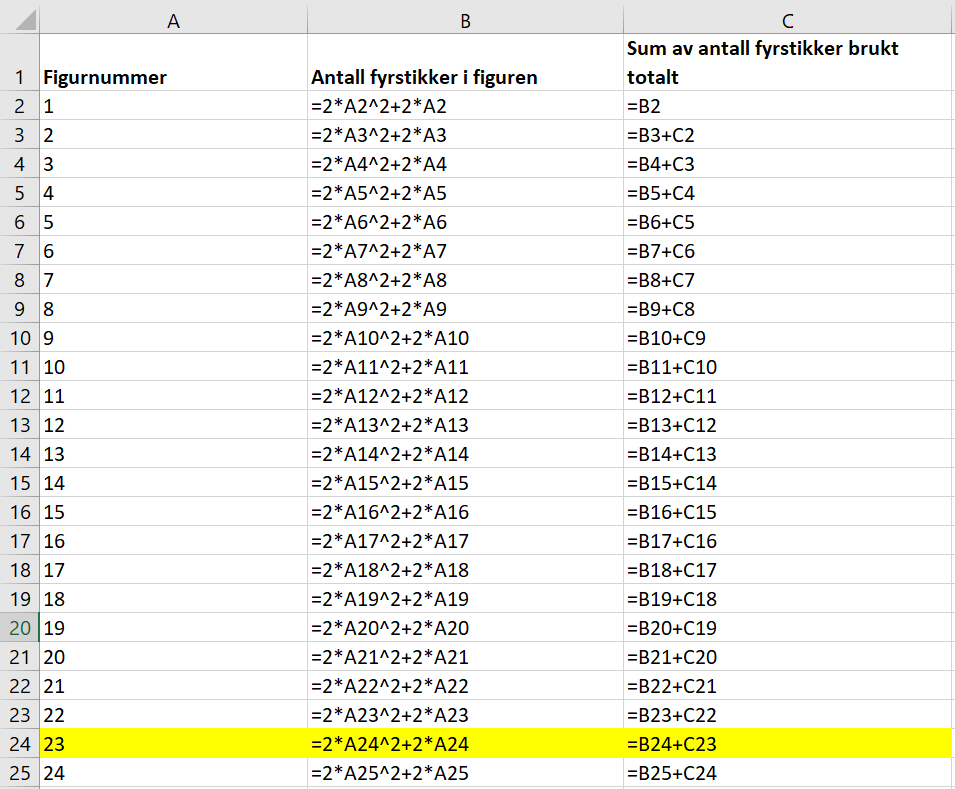
Løst med Excel:
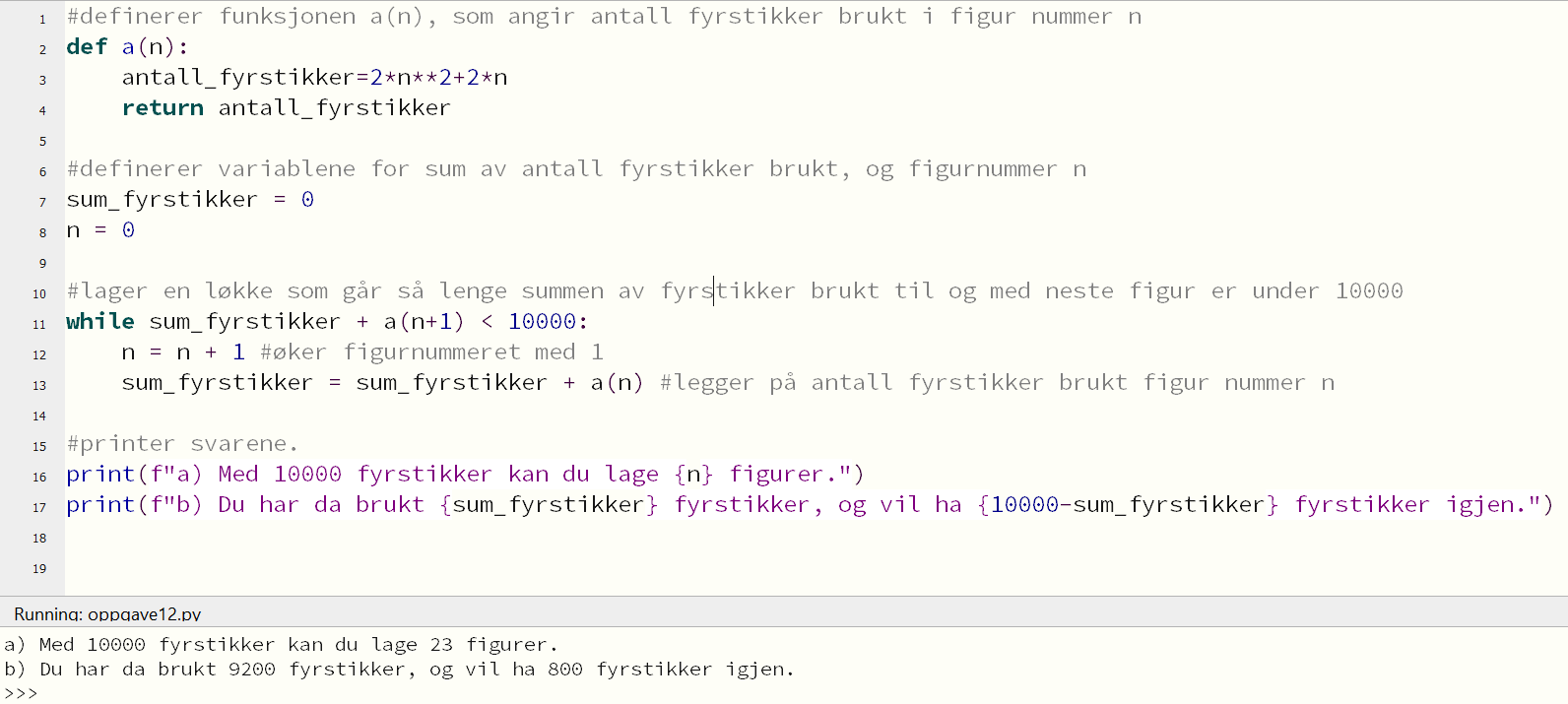
Løst med Python:
Programmerer en løkke i python som summerer antall brukte fyrstikker for hver figur, så lenge summen ikke overstiger 10000 fyrstikker.
a)
Med 10000 fyrstikker kan du lage 23 figurer.
b)
Når du har laget 23 figurer, har du brukt 9200 fyrstikker, og har dermed 800 fyrstikker igjen.
Oppgave 13
Stigningstallet for antall grader Farenheit som funksjon av antall grader Cesius er $\frac{9}{5}$. Det betyr at for en endring på én grad Celsius, endrer antall grader Farenheit med $\frac{9}{5}$. Det vil si at en endring på 5 grader Celsius tilsvarer en endring på 9 grader Farenheit. Påstanden om at en endring på 5 grader Celsius tilsvarer en endring på 41 grader Farenheit er altså feil.
Oppgave 14
For $x<0$ vil $x^2$ være et positivt tall, fordi multiplikasjonen av to negative tall gir et positivt produkt.
For $x<0$ vil $x^3$ være et negativt tall, fordi multiplikasjonen av tre negative tall gir et negativt produkt.
Når $x<0$ vil vi derfor alltid ha $x^2>x^3$, siden et positivt tall alltid er større enn et negativt tall.
Oppgavetype 3
Oppgave 15
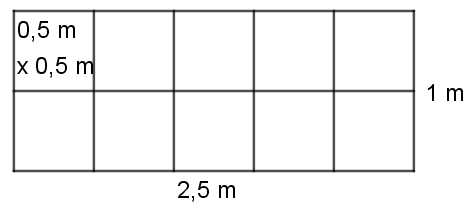
Jeg antar at en gjennomsnittlig person trenger gulvplass på ca. 50 cm x 50 cm.
Jeg tenker at det er plass til omtrent 10 personer, som vist på figuren under:
Det er mulig at det går an å trykke sammen flere personer i heisen, men det ville bli veldig trangt.
Oppgave 16
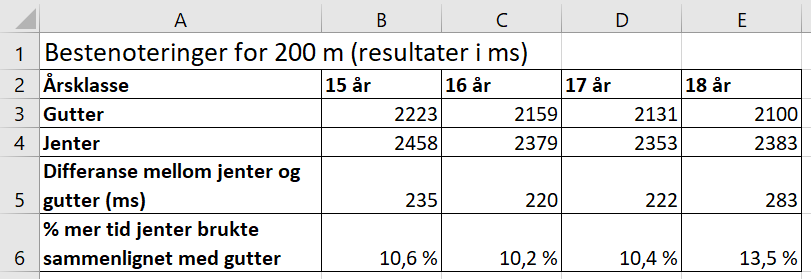
Bruker Excel for å sammenligne resultatene for gutter og jenter i ulike årsklasser.
Jeg ser at jentene i alle årsklasser bruker med tid enn guttene i samme årsklasse på 200 m løp. Jentene brukte omtrent 200-300 ms mer enn guttene, som tilsvarer at de brukte mer enn 10% mer tid enn guttene. Forskjellen var ganske like for årsklassene 15-17 år, men for årsklassen 18 år brukte jentene 13,5% mer tid enn guttene.