2P 2020 høst LØSNING: Forskjell mellom sideversjoner
| Linje 199: | Linje 199: | ||
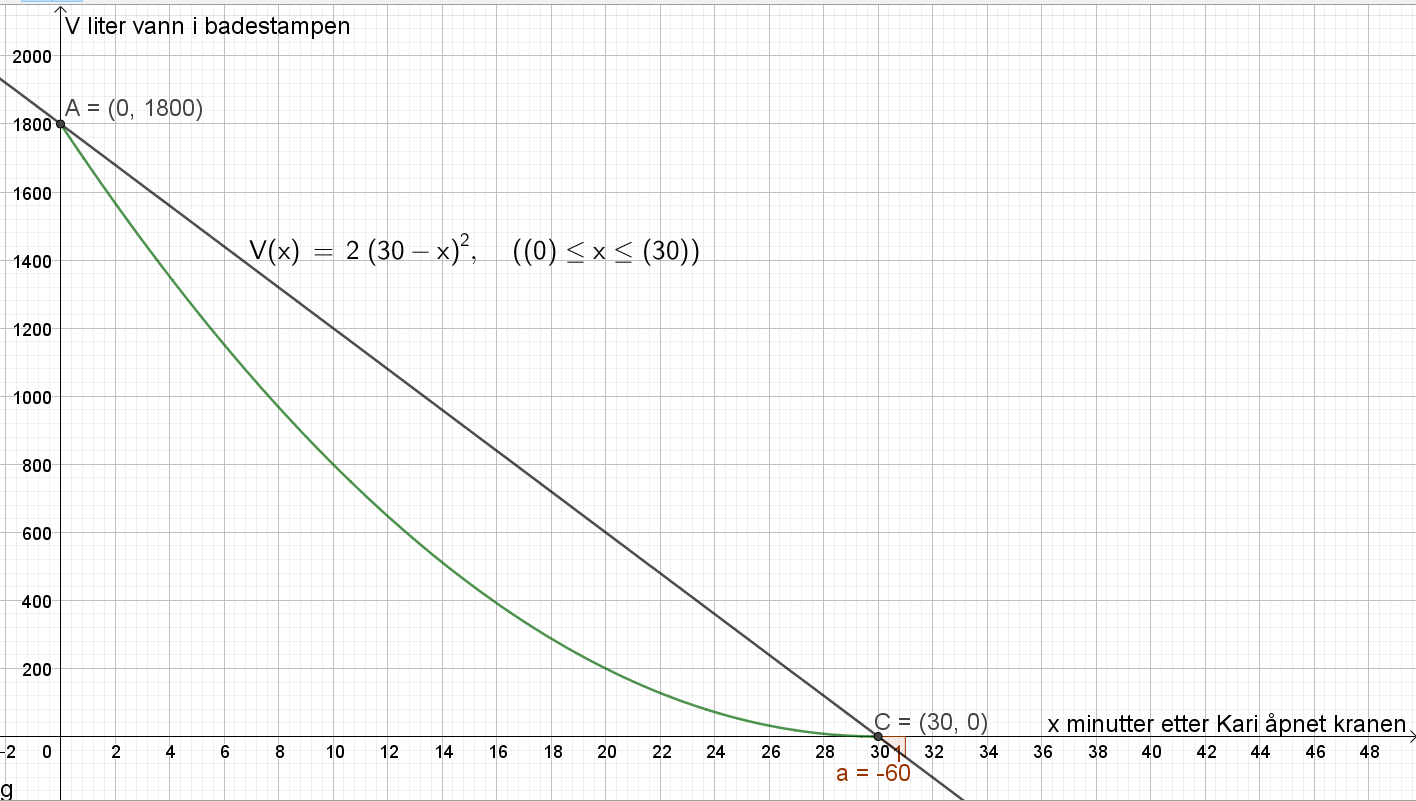
Finner skjæringspunktet med x-aksen, C=(30,0). Lager en linje som går gjennom punkt A og C, og finner stigningen til linjen. Stigningstallet a = -60. | Finner skjæringspunktet med x-aksen, C=(30,0). Lager en linje som går gjennom punkt A og C, og finner stigningen til linjen. Stigningstallet a = -60. | ||
[[File: | [[File: 2P_H20_del2_1c.png]] | ||
Det renner ut i gjennomsnitt 60 L vann per minutt fra Kari åpner kranen, til badestampen er tom. | Det renner ut i gjennomsnitt 60 L vann per minutt fra Kari åpner kranen, til badestampen er tom. | ||
===d)=== | ===d)=== | ||
Sideversjonen fra 2. des. 2020 kl. 18:01
Diskusjon av oppgaven på matteprat
Mer diskusjon av oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL 1
Oppgave 1
a)
Rangerer tallene i stigende rekkefølge:
$7\quad10\quad10\quad12\quad12\quad18\quad20\quad20\quad33\quad38$
Medianen er gjennomsnittet av de to midterste tallene: $\frac{12+18}{2}=\frac{30}{2}=15$
Gjennomsnitt: $\frac{7+10+10+12+12+18+20+20+33+38}{10}=\frac{180}{10}=18$
Medianen er 15 og gjennomsnittet er 18 for antall bilder som passerte i løpet av en periode med grønt lys.
b)
Hvis vi ser på den sorterte listen i a), ser vi at 18 er det sjette tallet. Det betyr at den kumulative frekvensen for 18 passerte biler er 6. Det forteller oss at det passerte 18 eller færre biler i løpet av en periode med grønt lys i 6 av observasjonene.
c)
Dersom tiden med grønt lys var kortet ned med 10 %, antar jeg at medianen og gjennomsnittet også ville synke med 10 %.
Ny median: $15-\frac{10\cdot 15}{100} = 15-1,5 = 13,5$ passerte biler i løpet av en periode med grønt lys.
Nytt gjennomsnitt: $18-\frac{10\cdot 18}{100}=18-1,8=16,2$ passerte biler i løpet av en periode med grønt lys.
Oppgave 2
$\frac{5\cdot 10^{12}+3,1\cdot 10^{13}}{1,8\cdot 10^7} = \frac{0,5\cdot 10^{13}+3,1\cdot 10^{13}}{1,8\cdot 10^7} = \frac{(0,5+ 3,1)\cdot 10^{13}}{1,8\cdot 10^7} = \frac{3,6\cdot 10^{13}}{1,8\cdot 10^7} = 2\cdot 10^{13-7} = 2\cdot 10^6 $
Oppgave 3
a)
| Høyde i cm | Klassemidtpunkt, $x_m$ | Frekvens, $f$ | $f\cdot x_m$ |
| $[150,160\rangle$ | $155$ | $10$ | $1550$ |
| $[160,170\rangle$ | $165$ | $30$ | $4950$ |
| $[170,180\rangle$ | $175$ | $50$ | $8750$ |
| $[180,200\rangle$ | $190$ | $10$ | $1900$ |
| Sum | $100$ | $17150$ |
Gjennomsnitt: $\frac{17150}{100}=171,5\,cm$
Gjennomsnittshøyden til elevene ved skolen er 171,5 cm.
b)
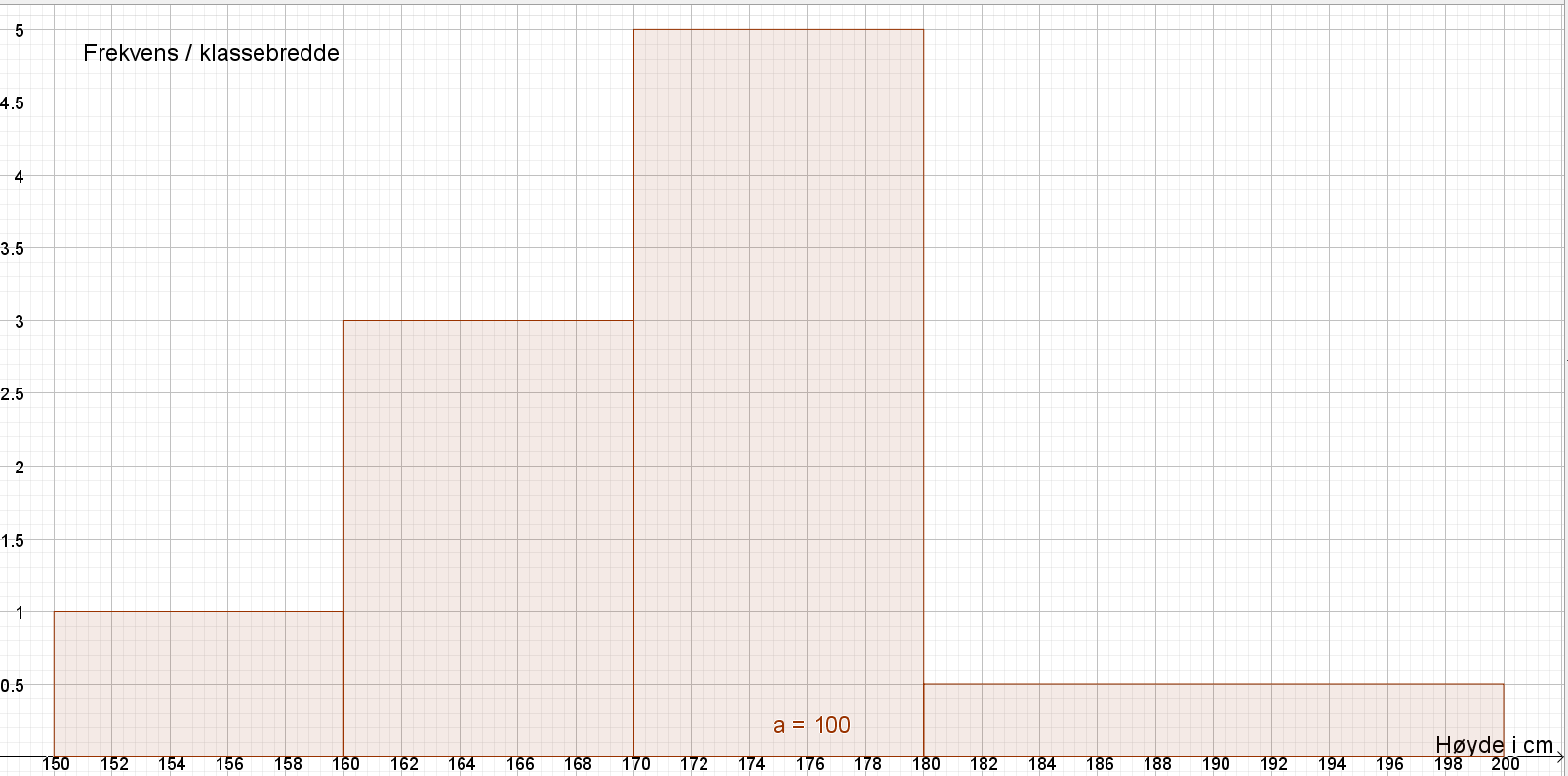
| Høyde i cm | Klassebredde, $b$ | Frekvens, $f$ | Histogramhøyde, $\frac{f}{b}$ |
| $[150,160\rangle$ | $160-150=10$ | $10$ | $\frac{10}{10}=1$ |
| $[160,170\rangle$ | $170-160=10$ | $30$ | $\frac{30}{10}=3$ |
| $[170,180\rangle$ | $180-170=10$ | $50$ | $\frac{50}{10}=5$ |
| $[180,200\rangle$ | $200-180=20$ | $10$ | $\frac{10}{20}=0,5$ |
PS: du må tegne histogrammet for hånd, siden dette er del 1.
Oppgave 4
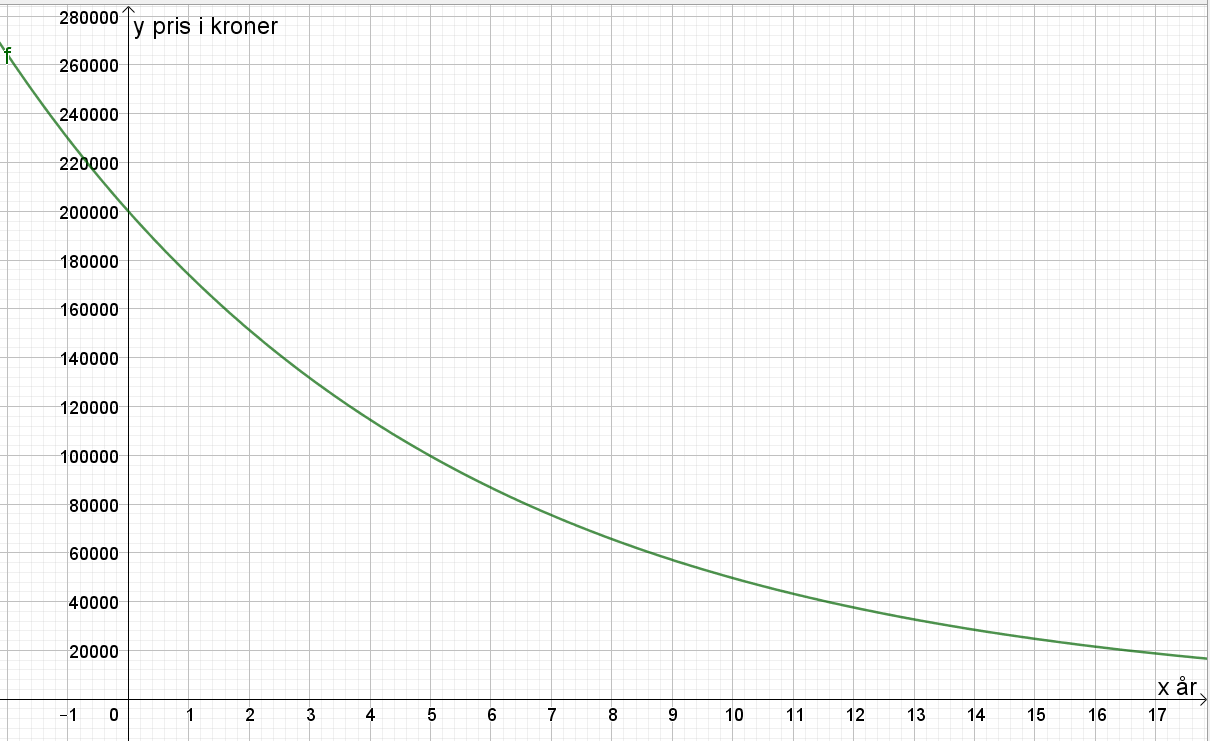
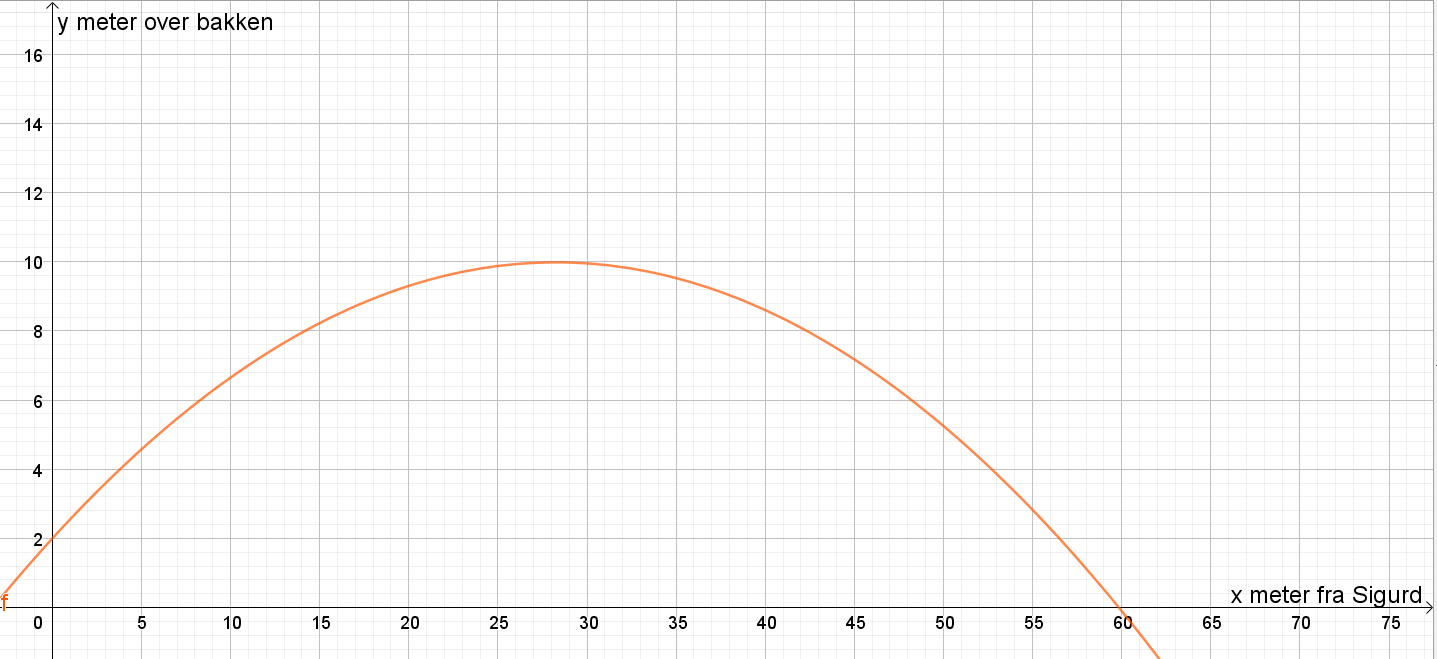
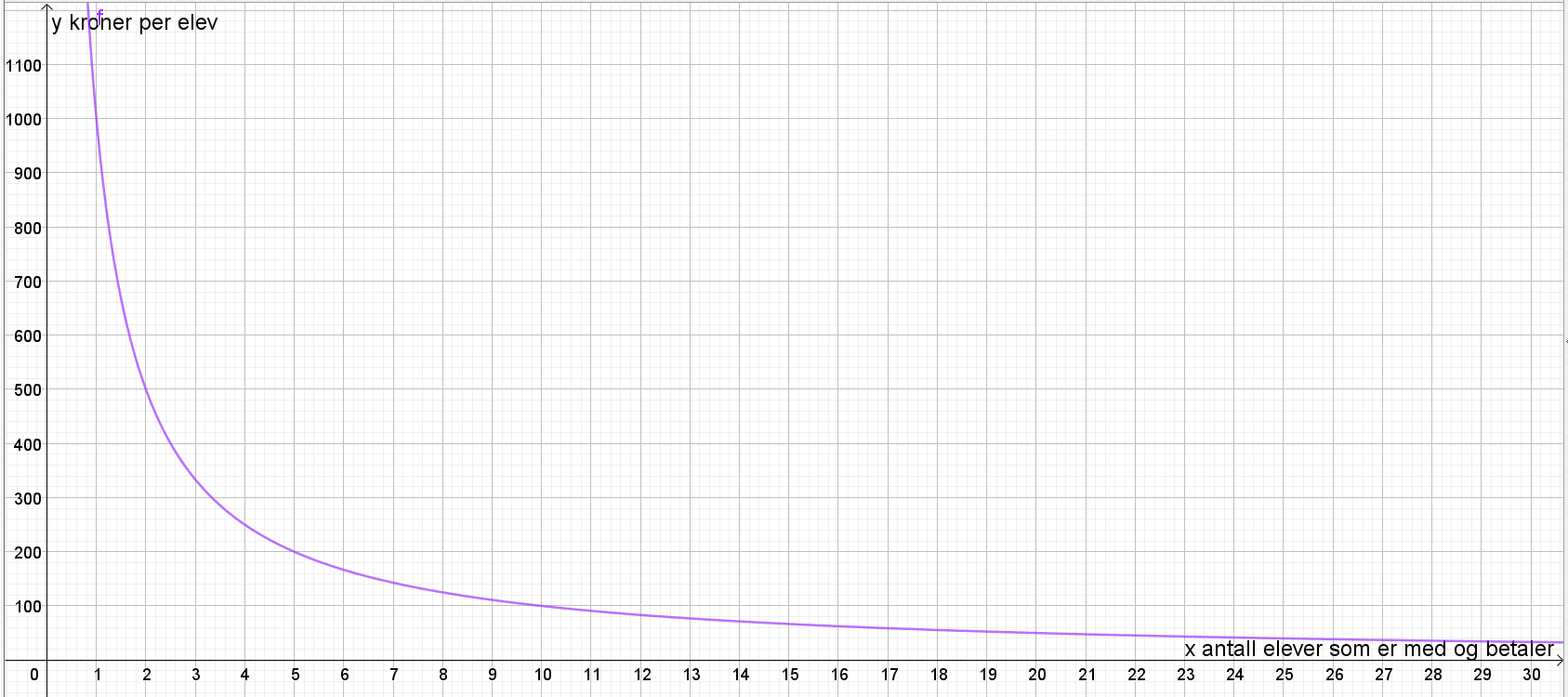
NB: siden dette er del 1, må du lage en skisse av disse grafene for hånd. Du må angi hvilke størrelser som er på x- og y-aksen, og skrive noen tall som passer på x- og y-aksen, spesielt i skjæringspunktene mellom grafen og aksene.
Situasjon 1: en eksponentiell modell beskriver bilens verdi som funksjon av x antall år.
Situasjon 2: en andregradsfunksjon beskriver spydets høyde som en funksjon av avstanden fra Sigurd.
Situasjon 3: en omvendt proporsjonal funksjon beskriver hvor mye hver elev må betale som funksjon av antall elever som blir med på gaven.
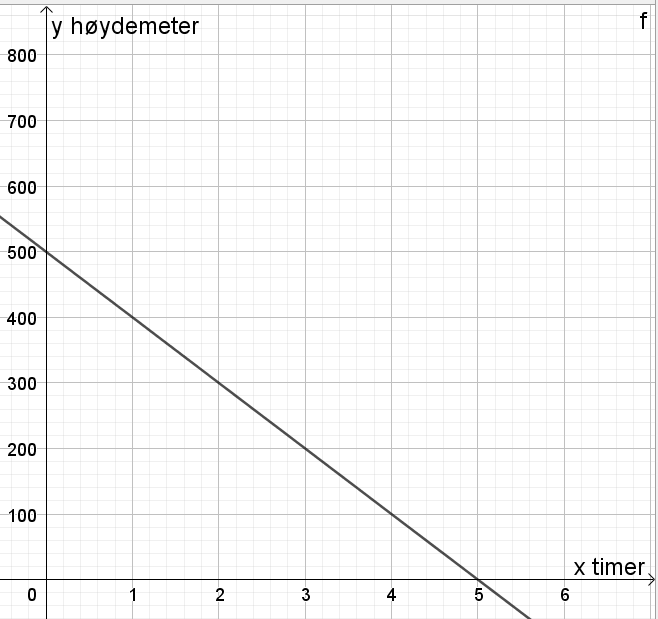
Situasjon 4: en lineær funksjon beskriver hvor mange høydemeter Ulrikke befinner seg på som funksjon av tiden.
Oppgave 5
Velger punktet (1989, 18 000) som startpunkt, og punktet (2019, 30 000) som sluttpunkt.
Finner stigningstallet til en rett linje som går gjennom de to punktene:
$a=\frac{y_2-y_2}{x_2-x_1}=\frac{30000-18000}{2019-1989}=\frac{12000}{30}=400$
En lineær modell som tilnærmet beskriver utviklingen i denne perioden er $y=400x+18000$, der x er antall år etter 1989.
Oppgave 6
a)
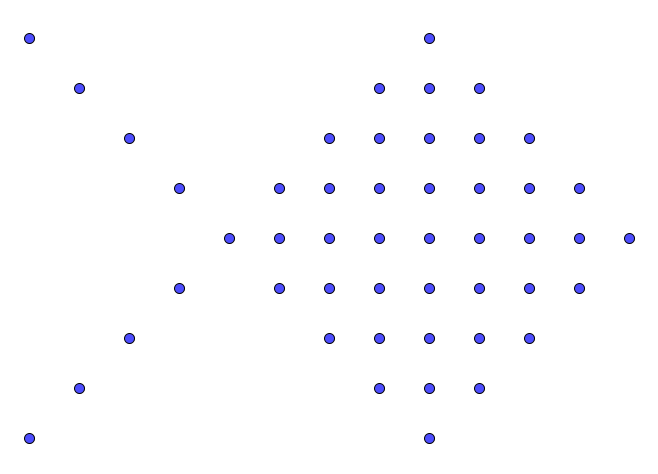
Tegner figur 4, og teller antall sirkler. Det vil være 49 sirkler i figur 4.
b)
Legger sammen lyse sirkler i "halen"+ lyse sirkler i "kroppen" + mørke sirkler for alle figurene, og prøver å finne et mønster.
Figur 1: $2+1+4 = 2\cdot1+1\cdot1+2\cdot2 = 7$
Figur 2: $4+4+9 = 2\cdot2+2\cdot2+3\cdot3 = 17$
Figur 3: $6+9+16 = 2\cdot3+3\cdot3+4\cdot4=31$
Figur 4: $8+16+25= 2\cdot4+4\cdot4+5\cdot5=49$
Figur n: $\quad 2\cdot n+n\cdot n+(n+1)\cdot(n+1) \\ =2n+n^2+ (n^2+2n+1) \\ = 2n^2+4n+1$
Antall sirkler i figur n kan uttrykkes ved $F_n=2n^2+4n+1$.
c)
$F_n=2n^2+4n+1 \\ F_{20} = 2\cdot 20^2 + 4\cdot 20 + 1 = 2\cdot 400+80+1=881$
Det vil være 881 sirkler i figur 20.
DEL 2
Oppgave 1
a)
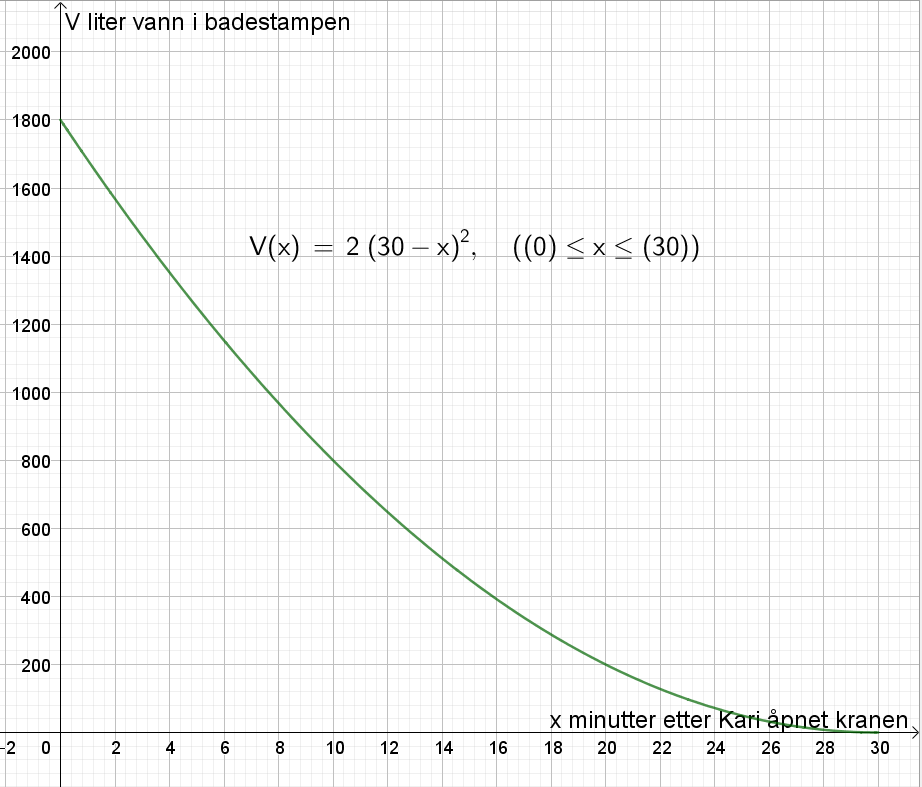
Tegner grafen til V i Geogebra.
b)
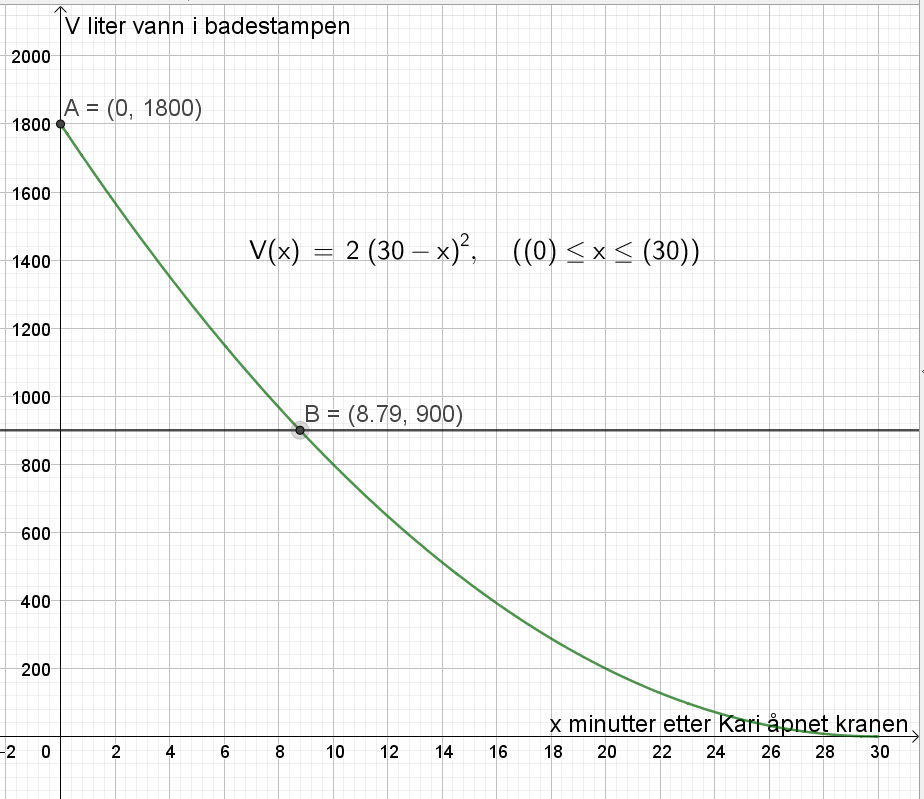
Finner skjæringspunktet med y-aksen, A=(0,1800). Det betyr at det var 1800 L vann i badestampen til å begynne med. 900 L tilsvarer da halvparten av vannet.
Lager linjen y = 900, og finner skjæringspunktet mellom denne linjen med grafen til V, B=(8.79, 900).
Det tar 8,79 minutter, det vil si omtrent 8 minutter og 47 sekunder, å tappe ut halvparten av vannet. ($0,79min\cdot 60sek/min=47 sek$).
c)
Finner skjæringspunktet med x-aksen, C=(30,0). Lager en linje som går gjennom punkt A og C, og finner stigningen til linjen. Stigningstallet a = -60.
Det renner ut i gjennomsnitt 60 L vann per minutt fra Kari åpner kranen, til badestampen er tom.