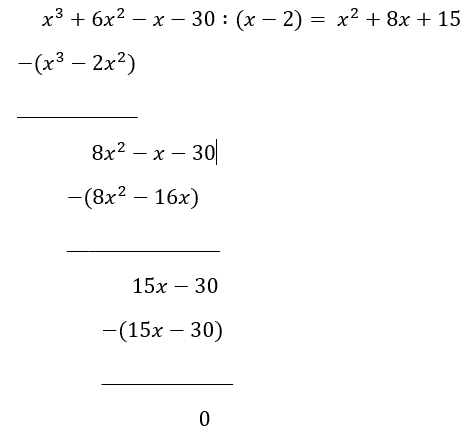R1 2018 høst LØSNING

Diskusjon av denne oppgaven på matteprat

Løsningsforslag (pdf) (open source, meld fra om forbedringer eller feil her)

Løsning del 1 laget av mattepratbruker mingjun

Løsning som PDF laget av Marius Nilsen ved Bergen Private Gymnas

Løsning til del 1 som videoer laget av Lektor Håkon Raustøl

DEL 1

Oppgave 1

a)

$f(x)=x^2+2x+e^x$

$f'(x)=2x+2+e^x$

b)

$g(x)=x^2\cdot ln \, x$

$g'(x)=2x\cdot ln \, x + x^2 \cdot \frac{1}{x} = 2x\cdot ln\, x + x$

c)

$h(x)=\frac{x-1}{e^{2x+1}}$

$h'(x)=\frac{1\cdot e^{2x+1}-(x-1)\cdot 2\cdot e^{2x+1}}{(e^{2x+1})^2} = \frac{1-(2x-2)}{e^{2x+1}} = \frac{-2x+1}{e^{2x+3}}$

Oppgave 2

a)

$e^{2x}+7e^x-8=0$

Setter $u=e^x$

$u^2+7u-8=0 \\ (u+8)(u-1)=0 \\ u=-8 \vee u=1 \\ e^x=-8 \vee e^x=1 \\ x= 0$

Ikke mulig å ta ln(-8), forkaster derfor det ene svaret.

b)

$ln(x^2-5x-1)-ln(3-2x)=0 \\ ln(x^2-5x-1)=ln(3-2x) \\ x^2-5x-1 = 3-2x \\ x^2-5x+2x-1-3 = 0 \\ x^2-3x-4=0 \\ (x+1)(x-4)=0 \\ x=-1 \vee x=4$

Setter inn hvert av svarene i likningen:

$ln((-1)^2-5(-1)-1) - ln(3-2(-1)) = 0 \\ ln(5)-ln(5)=0$

$x=-1$ er en løsning.

$ln(4^2-5\cdot 4-1)-ln(3-2\cdot 4)=0 \\ ln(-5)-ln(-5)=0$

$x=4$ er ikke en løsning fordi det ikke er mulig å ta ln(-5).

Oppgave 3

Vi har vektorene $\vec{a}=[2,3]$ og $\vec{b}=[-5,3]$

a)

$2\vec{b}-3\vec{a} = 2\cdot[-5,3]-3\cdot[2,3] = [-10,6]-[6,9] = [-16,-3]$

b)

$|\vec{a}|=\sqrt{2^2+3^2} = \sqrt{13}$

$|\vec{a}|<4$ fordi $\sqrt{16}=4$, og derfor er $\sqrt{13}<4$

c)

$\vec{a}\cdot \vec{b} = |\vec{a}|\cdot |\vec{b}|\cdot cos\,\alpha \\ cos \,\alpha = \frac{ \vec{a}\cdot \vec{b} } { |\vec{a}|\cdot |\vec{b}|} \\ cos \,\alpha = \frac{[2,3]\cdot[-5,3]}{\sqrt{13}\cdot \sqrt{(-5)^2+3^2}} \\ cos \,\alpha = \frac{-10+9}{\sqrt{13}\cdot \sqrt{34}} \\ cos \,\alpha = \frac{-1}{\sqrt{13}\cdot \sqrt{34}}$

Vi har $cos\,\alpha < 0$, hvilket betyr at vinkelen mellom de $\vec{a}$ og $\vec{b}$ er stump.

Oppgave 4

Vi har $f(x)=x^3+6x^2-x-30$

a)

$f(2)=2^3+6\cdot 2^2-2-30 = 8+24-2-30 = 0$

$x=2$ er et nullpunkt, så divisjonen $f(x):(x-2)$ går opp.

b)

Utfører polynomdivisjonen:

Faktoriserer uttrykket:

$x^3+6x^2-x-30 = (x^2+8x+15)(x-2) = (x+5)(x+3)(x-2)$

c)

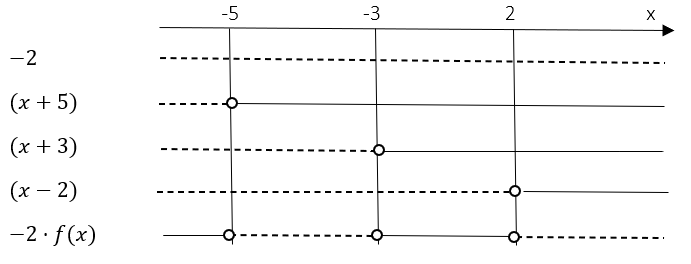
$-2\cdot f(x) \geq 0 \\ -2(x+5)(x+3)(x-2) \geq 0 $

$-2\cdot f(x) \geq 0$ når $x\in \langle \leftarrow, -5] \cup [-3,2]$

Oppgave 5

a)

Edelgran = E, Kvinne = K, Mann = M

$P(E) = P(E|M)\cdot P(M)+P(E|K)\cdot P(K) \\ = 0,60\cdot 0,70 + 0,40\cdot 0,30 = 0,42 + 0,12 = 0,54$

Sannsynligheten for at det første treet han selger en dag, er edelgran, er 0,54.

b)

$P(K|E) = \frac{P(K)\cdot P(E|K)}{P(E)} = \frac{0,30\cdot 0,40}{0,54} = \frac{0,12}{0,54} = \frac{12}{54} = \frac{2\cdot 6}{9\cdot 6} = \frac{2}{9}$

Sannsynligheten for at vinneren av lotteriet blir en kvinne, er $\frac{2}{9}$.