R1 2020 vår LØSNING: Forskjell mellom sideversjoner
| Linje 158: | Linje 158: | ||
Banefarten til partikkel 1 blir da: $ | \vec{v_1(-1) }| = \sqrt{4 +1} = \sqrt 5$ | Banefarten til partikkel 1 blir da: $ | \vec{v_1(-1) }| = \sqrt{4 +1} = \sqrt 5$ | ||
Banefart partikkel 2: $ | \vec{v_2(-1) }| = \sqrt{4 +144 = \sqrt{148}$ | |||
===c)=== | ===c)=== | ||
Sideversjonen fra 23. jun. 2020 kl. 04:35
Diskusjon av denne oppgaven på matteprat
Løsningsforslag til del 1 av Kristian Saug
Løsningsforslag del 2 av Kristian Saug
Løsningsforslag av Svein Arneson
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL EN
Oppgave 1
a)
$f(x)=x^6 + 3x^5 + ln(x) \\ f'(x)= 6x^5+15x^4 + \frac{1}{x}$
b)
$g(x)=2x^2 \cdot e^{2x-1}\\ g'(x) = 4x \cdot e^{2x-1} + 2x^2 \cdot 2 \cdot e^{2x-1} = (1+x)4x \cdot e^{2x-1}$
c)
$h(x) = \frac{4x-1}{x+2} \\ h'(x) = \frac{4(x+2) - (4x-1)}{(x+2)^2} = \frac{9}{(x+2)^2}$
Oppgave 2
a)
$ln(x^2) + ln(x) = 12 \\ 2 ln(x) + ln(x) = 12 \\ 3 ln(x) = 12 \\ e^{ln(x)} = e^4 \\ x = e^4 $
b)
$e^{2x}-e^x =6 \\(e^x)^2 - e^x - 6 =0 \\ u = e^x \\ u^2-u-6=0 \\ u = 3 \vee u = -2 \\ e^x = 3 \vee e^x = -2 \\ x = ln(3)$
$e^x =-2$ har ingen løsning.
Oppgave 3
$\vec{u} \cdot \vec{v } =-2$ og $|\vec u | = 3$ og $ |\vec v | = 2$
$\vec a = 2 \vec u + 3 \vec v$ og $ \vec b = t \cdot \vec u + 5 \vec v$
a)
Dersom to vektorer er parallelle:
$ k \vec{a} = \vec{b} \\ k(2 \vec u + 3 \vec v) = t \cdot \vec u + 5 \vec v \\ 2k \vec u = t \cdot u \wedge 3k \cdot \vec v = 5 \vec v \\ t = 2k \wedge k = \frac 53 \\ t = \frac{10}{3}$
b)
Når to vektorer står normalt på hverandre er skalarproduktet null:
$ (2 \vec{ u} + 3 \vec {v})(t \cdot \vec u + 5 \vec v )= 0 \\ 2 \cdot t \cdot \vec {u^2} + 10 \cdot \vec{ u} \cdot \vec v + 3 \cdot t \cdot \vec u \cdot \vec v + 15 \vec{ v^2}$
Setter inn alt som er oppgitt i oppgaven og får:
$2 \cdot 9 \cdot t $
Oppgave 4
a)
Dersom polynomet går opp i (x-1) må P(1) være lik null:
$P(1) = 6 \cdot 1^3-5 \cdot 1^2-2 \cdot 1 +1 = 6-5 -2+1=0$, altså går divisjonen P(x) : (x-1) opp.
b)
c)
d)
$P(x)= (x-1)(2x+1)(3x-1)$ og $F(x)= \frac{P(x)}{x^2-1} = \frac{(x-1)(2x+1)(3x-1)}{(x+1)(x-1)}$
Oppgave 5
Oppgave 6
a)
AB har lengden 6 og DC har lengden 2x. Høyden er f(x):
$F(x) = \frac{6+2x}{2} \cdot (9-x^2) = -x^3 - 3x^2 +9x+ 27$
b)
$F'(x) = -3x^2-6x+9$
$F'(x) = 0 $ gir x= -3 eller x = 1.
Av uttrykket for den deriverte ser man at den deriverte går fra positv til negativ i nullpunktet x = 1 ( parabelen vender sin hule side ned.)
$F(1)= -1-3 + 9 + 27 = 32$
Oppgave 7
Vinkel D er 65 grader, da er vinkel w = 130 grader. (periferi / sentral vinkel) Av samme grunn er u = 65 grader. I trekanten BCE er vinkelen i E (180-35-65) grader = 80 grader. Det gjør at vinkel v = 100 grader.
Oppgave 8
DEL TO
Oppgave 1
a)
Tellingen av en bil skal ikke påvirke den neste. Dersom hun teller bilene i en "elbil kortesje" blir det feil. Hun må anta at populasjonen av biler er stor i forhold til de 100 hun teller, slik at det ikke endrer sannsynligheten (man kan tenke at å telle en bil er det samme som å trekke ut, uten tilbakelegging. Dersom populasjonen er stor i forhold til utvalget vil ikke sannsynligheten påvirkes i nevneverdig grad.)
b)
c)
Oppgave 2
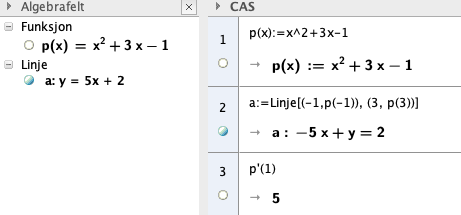
a)
Begge linjene har stigningstall 5, altså er de parallelle.
b)
Som skulle vises.
Oppgave 3
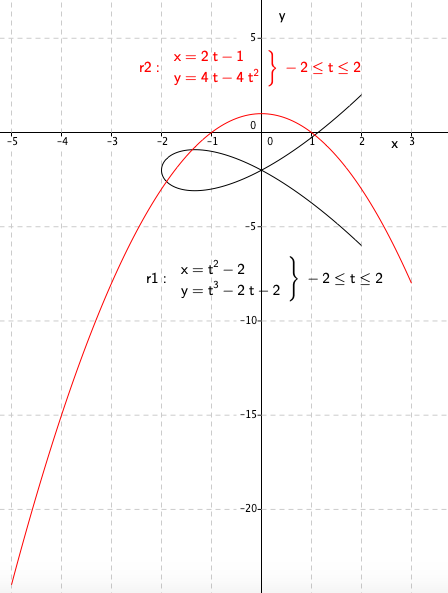
a)
b)
Vi finner fartsvektorene ved å derivere posisjonsvektorene:
$\vec{v_1 (t)} = (\vec{r_1(t)})' = [2t,3t^2-2 ] \\ \vec{v_2 (t)} = (\vec{r_2(t)})' = [2,4-8t ]$
Banefarten til partikkel 1 blir da: $ | \vec{v_1(-1) }| = \sqrt{4 +1} = \sqrt 5$
Banefart partikkel 2: $ | \vec{v_2(-1) }| = \sqrt{4 +144 = \sqrt{148}$