1T 2020 vår LØSNING

oppgaven som pdf

Diskusjon av denne oppgaven på matteprat

Løsningsforslag til del 1 laget av Kristian Saug

Løsningsforslag til del 2 laget av Kristian Saug

Løsningsforslag til del 1 og 2 laget av Svein Arneson

DEL 1

Oppgave 1

$\frac{5,5\cdot 10^{-7}+0,4\cdot 10^{-6}}{0,005} \\= \frac{5,5\cdot 10^{-7}+4\cdot 10^{-7}}{0,005} \\= \frac{(5,5+4)\cdot 10^{-7}}{5\cdot 10^{-3}} \\= \frac{9,5\cdot 10^{-7}}{5\cdot 10^{-3}} \\= 1,9\cdot 10^{-7-(-3)} \\= 1,9\cdot 10^{-4}$

Et tips for å regne ut $\frac{9,5}{5}$ er å gange teller og nevner med 2, slik at du får 10 i nevner, som er lettere å regne ut:

$\frac{9,5}{5}=\frac{9,5\cdot 2}{5\cdot 2}=\frac{19}{10}=1,9$

Oppgave 2

Finner stigningstallet a:

$a = \frac{y_2-y_1}{x_2-x_1} = \frac{0-6}{4-2} = \frac{-6}{2} = -3$

Finner likningen for linja ved ettpunktsformelen:

$y-y_1 = a(x-x_1) \\ y-0 = -3(x-4) \\ y=-3x+12$

Oppgave 3

Bruker innsetningsmetoden.

Uttrykker likning 1 ved y:

$2x+y=3 \\ y=3-2x$

Setter inn uttrykket for y i likning 2:

$8x-2y=-12 \\ 8x-2(3-2x)=-12 \\ 8x-6+4x=-12 \\ 12x = -12+6 \\ x = \frac{-6}{12} \\ x = - \frac{1}{2}$

Finner verdien av y ved hjelp av uttrykket mitt for y:

$y = 3-2x \\ y= 3-2\cdot(-\frac{1}{2}) \\ y = 3+1 \\ y=4$

Løsning: $x = -\frac{1}{2}$ og $y=4$

Oppgave 4

$\frac{2}{x-2}-\frac{x-4}{x^2-5x+6}$

$=\frac{2}{x-2}-\frac{x-4}{(x-2)(x-3)}$

$=\frac{2(x-3)}{(x-2)(x-3)}-\frac{x-4}{(x-2)(x-3)}$

$=\frac{2x-6-x+4}{(x-2)(x-3)}$

$=\frac{x-2}{(x-2)(x-3)}$

$=\frac{1}{x-3}$

Oppgave 5

$2x^2+12x+18 \leq 0$

$=2(x^2+6x+9) \leq 0$

$=2(x+3)(x+3) \leq 0$

$=2(x+3)^2 \leq 0$

Utrykket $(x+3)^2=0$ for $x= -3$. For alle andre x-verdier er uttrykket positivt.

Den eneste løsningen av ulikheten $2x^2+12x+18 \leq 0$ er $x = -3$.

Oppgave 6

$\frac{\sqrt{45}+\sqrt{80}}{\sqrt{125}}$

$=\frac{\sqrt{9\cdot 5}+\sqrt{16\cdot 5}}{\sqrt{25\cdot 5}}$

$=\frac{3\sqrt{5}+4\sqrt{5}}{5\sqrt{5}}$

$=\frac{7\sqrt{5}}{5\sqrt{5}}$

$=\frac{7}{5}$

Oppgave 7

$9^2\cdot 3^{-3}\cdot 8^{\frac{1}{3}}\cdot 27^{-\frac{2}{3}}$

$=(3^2)^2\cdot 3^{-3}\cdot (2^3)^{\frac{1}{3}}\cdot (3^3)^{-\frac{2}{3}}$

$=3^4\cdot 3^{-3}\cdot 2^1\cdot3^{-2}$

$=3^{4-3-2}\cdot 2$

$=3^{-1} \cdot 2$

$=\frac{2}{3}$

Oppgave 8

$lg10+lg0,1+lg\frac{1}{100}+lg\sqrt[3]{10}$

$=1+(-1)+(-2)+\frac{1}{3}lg10$

$=-2+\frac{1}{3}\cdot 1$

$=\frac{-6}{3}+\frac{1}{3}$

$=-\frac{5}{3}$

Oppgave 9

a)

$lg(\frac{3x+3}{3})=3$

$\frac{3x+3}{3}=10^3$

$3x+3 = 1000\cdot 3$

$3x = 3000-3$

$x = \frac{2997}{3}$

$x = 999$

b)

$3^{x^2}\cdot 3^{-4x}=1$

$3^{x^2-4x}=3^0$

$x^2-4x=0$

$x(x-4)=0$

$x=0 \vee x=4$

Oppgave 10

Arealet av det skraverte området kan uttrykkes ved:

1) $(a-b)(a-b)=(a-b)^2$

2) $a^2-ab-ab+b^2=a^2-2ab+b^2$

Figuren illustrerer andre kvadratsetning.

Oppgave 11

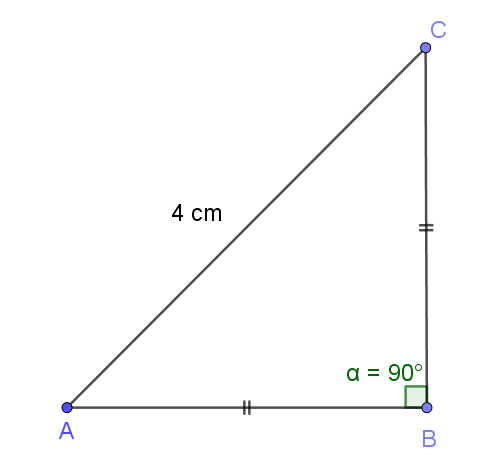
Siden $tan\angle A = 1$, er katetene i denne rettvinklede trekanten like store.

Brukes Pytagorassetningen til å finne lengden av katetene, AB og BC, som er like store:

$x^2+x^2=4^2$

$2x^2 = 16$

$x^2 = 8$

$x=\sqrt{8} = 2\sqrt{2}$

$AB = BC = 2\sqrt{2}$

Oppgave 12

$P(2,4)+P(4,2)= \frac{1}{10}\cdot \frac{1}{10} + \frac{1}{10}\cdot \frac{1}{10} = \frac{1}{100}+\frac{1}{100} = \frac{2}{100} = 0,02$

Sannsynligheten for at koden begynner på 2 4 eller 4 2 er 0,02.

Oppgave 13

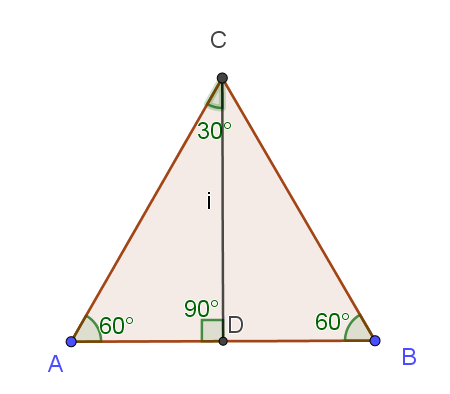
a)

Vi lager en midtnormal på AB, slik at vi får trekanten ADC. I en trekant der vinklene er $30^{\circ}, 60^{\circ}$ og $90^{\circ}$, er den korteste kateten halvparten av lengden til hypotenusen. Vi har da:

$sin \angle DCA = \frac{1}{2}$

$sin30^{\circ} = \frac{1}{2}$