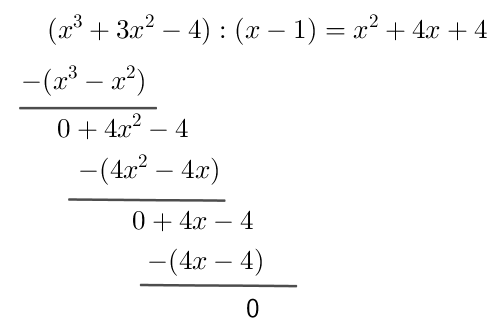S2 2019 høst LØSNING

oppgaven som pdf

diskusjon av oppgaven på matteprat

Løsningsforslag til del 2 laget av mattepratbruker Krisian Saug

Løsningsforslag del 1 og del 2 laget av Svein Arneson

DEL 1

Oppgave 1

a)

$f(x)=\frac{1}{2}\ln{x}$

$f'(x)=\frac{1}{2x}$

b)

$g(x)=3x\cdot e^{2x}$

$g'(x)=3\cdot e^{2x}+3x\cdot 2\cdot e^{2x} \\ g'(x)=3e^{2x} (2x+1)$

c)

$h(x)=\frac{x^2+1}{x-3}$

$h'(x)=\frac{2x\cdot (x-3) - (x^2+1)\cdot 1}{(x-3)^2} \\ h'(x)=\frac{2x^2-6x-x^2-1}{x^2-6x+9} \\ h'(x)=\frac{x^2-6x-1}{x^2-6x+9}$

Oppgave 2

a)

$a_n=a_1+(n-1)\cdot d \\ a_4=a_1+(4-1)\cdot d \\ 7=-8+3d \\ 3d=15 \\ d=5$

$a_n=-8+(n-1)\cdot 5 \\ a_n=-8+5n-5 \\ a_n=5n-13$

b)

$a_{40}=5\cdot 40-13=200-13=187$

$S_n=\frac{a_1+a_n}{2}\cdot n \\ S_{40}=\frac{-8+187}{2}\cdot 40 \\ S_{40}=179\cdot 20 \\ S_{40}=3580$

Oppgave 3

a)

$a_n=a_1\cdot k^{n-1}$

For denne rekka har vi:

$a_n=6\cdot (-\frac{1}{2})^{n-1}$

Dersom $-1<k<1$ i en geometrisk tallfølge $a_n=a_1k^{n-1}$ sier vi at den konvergerer. I dette tilfelle er $k=-\frac{1}{2}$, så rekken konvergerer.

I slike tilfeller er summen $S=\frac{a_1}{1-k}$.

$S=\frac{6}{1-(-\frac{1}{2})} = \frac{6}{\frac{3}{2}} = \frac{6\cdot 2}{3}=4$

b)

$0,135135135... = 0,135 + 1,000135 + 0,000000135 + … = \frac{135}{1000} +\frac{135}{1000^2}+\frac{135}{1000^3}+...$

Dette kan uttrykkes som en geometrisk rekke:

$a_n=\frac{135}{1000} \cdot (\frac{1}{1000})^{n-1}$

Vi har $-1<k<1$, så denne rekken konvergerer. Summen av den geometriske rekken, altså tallet $0,135135135...$ blir da:

$S=\frac{a_1}{1-k}=\frac{\frac{135}{1000}}{1-\frac{1}{1000}} = \frac{\frac{135}{1000}}{\frac{999}{1000}} = \frac{135}{999}=\frac{45}{333}=\frac{15}{111}=\frac{5}{37}$

Det kan være vanskelig å vite at teller og nevner i $\frac{135}{999}$ er delelig på 27, så jeg deler teller og nevner på 3, i tre omganger.

$0,135135135...=\frac{5}{37}$

Oppgave 4

I. $a\cdot x-2y+z=4$

II. $2x+z=6$

III. $3x+3y+z=7$

Setter inn $x=-2$ i likning II.

II. $2\cdot (-2)+z=6 \\ z=6+4\\z=10$

Setter inn $x=-2$ og $z=10$ i likning III.

III. $3\cdot(-2)+3y+10=7 \\ 3y=7-10+6 \\ y=\frac{3}{3}\\y=1$

Setter inn $x=-2$, $y=1$ og $z=10$ i likning I.

I. $a\cdot (-2)-2\cdot 1 + 10=4 \\ -2a=4-10+2 \\ a=\frac{-4}{-2} \\ a=2$

Oppgave 5

$f(x)=x^3+3x^2-4$

a)

$f(x)=x^3+3x^2-4=(x^2+4x+4)(x-1)=(x+2)^2\cdot (x-1)$

b)

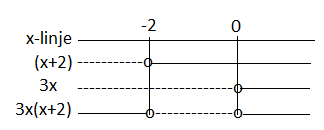
$f'(x)=3x^2+6x=3x(x+2)$

Finner x-verdiene i ekstremalpunktene:

$f'(x)=0 \\ 3x(x+2)=0 \\ x=-2 \vee x=0$

Finner y-verdiene i ekstremalpunktene:

$f(-2)=(-2)^3+3\cdot (-2)^2-4 = -8+12-4=0$

$f(0)=0^3+3\cdot 0^2-4=-4$

Funksjonen $f$ har et toppunkt i $(-2,0)$ og et bunnpunkt i $(0,-4)$

c)

$f'\, '(x)=6x+6$

Finner x-verdien i vendepunktet:

$f'\, '(x)=0 \\ 6x+6=0 \\ x=-1$

Finner y-verdien i vendepunktet:

$f(-1)=(-1)^3+3\cdot(-1)^2-4=-1+3-4=-2$

Finner den deriverte i vendepunktet:

$a=f'(-1)=3\cdot(-1)^2+6\cdot(-1)=3-6=-3$

Finner vendetangenten:

$(y-y_1)=a\cdot(x-x_1) \\ y-(-2)=-3(x-(-1)) \\ y+2=-3x-3 \\ y=-3x-5$

d)

Husk at dette må gjøres for hånd på eksamen.

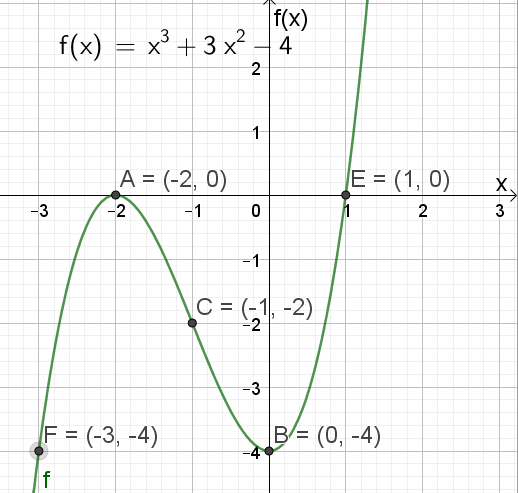
Har ekstremalpunktene A=(-2,0) og B=(0,-4), samt vendepunktet C=(-1, -2) fra før.

Finner f(-3) og f(1) i tillegg.

$f(-3)=(-3)^3+3\cdot (-3)^2-4=-27+27-4=-4$

$f(1)=1^3+3\cdot 1^2-4=1+3-4=0$

Vi har nå også punktene E=(1,0) og F=(-3,-4). Det holder for en skisse.

e)

Fra før av har vi nullpunktene til funksjonen $f$, A=(-2,0) og E=(1,0). Setter $u=\ln{x}$.

$(\ln{x})^3+3(\ln{x})^2-4=0 \\ u^3+3u^2-4=0 \\ u=-2 \vee u=1$

$\ln{x}=-2 \vee \ln{x}=1 \\ x=e^{-2} \vee x=e$

Oppgave 6

$h(t)=\frac{100}{1+a\cdot e^{-0,0693\cdot t}}$

a)

$h(0)=20 \\ \frac{100}{1+a\cdot e^{-0,0693\cdot 0}}=20 \\ \frac{100}{1+a\cdot 1}=20 \\ 100=20\cdot(1+a) \\ 100 = 20+20a \\ a=\frac{80}{20} \\ a=4$

b)

Tallet 100 er den verdien h(t) konvergerer mot når t går mot uendelig. Dette fordi nevneren vil nærme seg 1 når t går mot uendelig (fordi $e^{-\infty}\approx 0$), og brøken får da tellerens verdi.

Etter mange år vil altså antall gås på øya stabilisere seg på 100.

c)

Siden $h'\, '(20)=0$, er vendepunktet til funksjonen i $t=20$. Vendepunktet er der veksten er raskest.

Hekkebestanden øker raskest etter 20 år.

Oppgave 7

a)

$E(X)=0\cdot 0,45 + 1\cdot 0,30+2\cdot0,10+3\cdot0,10+4\cdot0,05=0,30+0,20+0,30+0,20=1$

E(X) forteller oss at vi kan forvente 1 skade på et tilfeldig valgt epletre.

b)

$VAR(X)=(0-1)^2\cdot0,45+(1-1)^2\cdot0,30+(2-1)^2\cdot0,10+(3-1)^2\cdot0,10+(4-1)^2\cdot0,05 \\ =0,45+0,10+0,40+0,45=1,4$

c)

S er summen av X antall skader på 400 uavhengige tilfeldige valg av trær. Sentralgrensesetningen sier at for et stort antall forsøk (slik som 400) er S tilnærmet normalfordelt.

$E(S)=n\cdot E(X)=400\cdot 1=400$

$STDAV(S)=\sqrt{400}\cdot STDAV(X)=\sqrt{400}\cdot \sqrt{VAR(X)}=\sqrt{400}\cdot\sqrt{1,4}$

$VAR(S)=(STDAV(S))^2=400\cdot 1,4=560$