Bokstavuttrykk: Forskjell mellom sideversjoner

Sideversjonen fra 19. jun. 2010 kl. 17:19

Innledning

Algebra, eller bokstavregning, viser generelle sammenhenger. Tallregning eller aritmetikk gir oss mer spesielle sammenhenger.
Eksempel: En sirkel har radius 10 cm. Hva er arealet av sirkelen?
Arealet blir:
<tex>A = 10cm \cdot 10cm \cdot {\pi} =314,2 cm^2.</tex>
Men, det gjelder bare når radius i sirkelen er 10 cm. For alle andre radier er dette arealet feil.

Et areal som gjelder for en sirkel, uansett radius:
<tex>A = {\pi}r^2</tex>
Man kan sette inn den verdi man ønsker for radien r og derved få arealet A for en hvilket som helst radius.
Bokstaver gir en formel som er allmenngyldig mens aritmetikken (tallregning)fokuserer på en eller flere spesielle tallverdier.

Ledd

Se på uttrykket <tex>a + b + 4</tex>

Uttrykket består av tre ledd

Et ledd er en verdi i et regnestykke som er adskilt fra resten med et pluss eller minus.De tre leddene er a,b og 4

<tex>10a^2 + 2b + 2 \cdot 2</tex>
er også et uttrykk som består av tre ledd der hvert av leddene er produkter av to eller flere faktorer.

Produkt

Av og til skrives ikke multiplikasjonstegnet mellom faktorene; a•b skrive ofte som ab og g•(h+f) skrives gjerne som g(h+f). Selv om man ikke skriver multiplikasjonstegnet er det der allikevel.

Når man regner med tall og parenteser har man muligheten til å trekke sammen parentesene før man løser de opp, i algebra er denne muligheten begrenset da man ikke uten videre kan trekke sammen for eksempel a + b. Før du går løs på regning med bokstaver er det derfor viktig at du kjenner reglene for regning med parenteser.

Alle regneregler du kjenner fra tallregning gjelder også for algebra. La oss se på noen regler:

Regneregler

Kommutativ lov:

<tex>a + b = b + a </tex>

Assosiativ lov:

<tex>(a + b) + c = a + (b + c)</tex>

Kommutativ lov:

<tex>a \cdot b = b \cdot a </tex>

<tex>a + a = 2a </tex>

Test deg selv

Kvadratsetningene

De neste tre setningen kalles for kvadratsetningene.

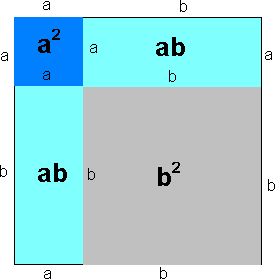
Første kvadratsetning

<tex>(a+b)^2 = (a+b)(a+b)= a^2+2ab+b^2 </tex>

Eksempel:

<tex>(3x+y)^2 = (3x+y)(3x+y)= 9x^2 + 6xy + y^2 </tex>

Det er nyttig å kunne regne ut kvadratet på denne måten når du skal forenkle utrykke ved å trekke sammen ledd. Man må også beherske kvadratsetningene andre veien, det er nødvendig ved forkorting av brøker. For å kunne forkorte et utrykk må det være på faktorform. Dette krever litt trening i å "se" hva produktet blir.

Eksempel:

<tex> 16a^2 + 24ab + 3b = (4a + 3b)^2</tex>

Test deg selv

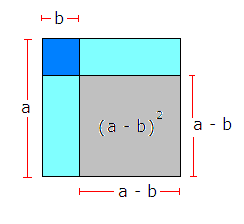
Andre kvadratsetning

<tex>(a - b)^2 = (a - b)(a-b)= a^2-2ab+b^2 </tex>

Eksempel:

<tex>(3x-y)^2 = (3x-y)(3x-y)= 9x^2 - 6xy + y^2 </tex>

Det er nyttig å kunne regne ut kvadratet på denne måten når du skal forenkle utrykke ved å trekke sammen ledd. Man må også beherske kvadratsetningene andre veien, det er nødvendig ved forkorting av brøker. For å kunne forkorte et utrykk må det være på faktorform. Dette krever litt trening i å "se" hva produktet blir.

Eksempel:

<tex> 16a^2 - 24ab + 9b^2 = (4a - 3b)^2</tex>

Test deg selv

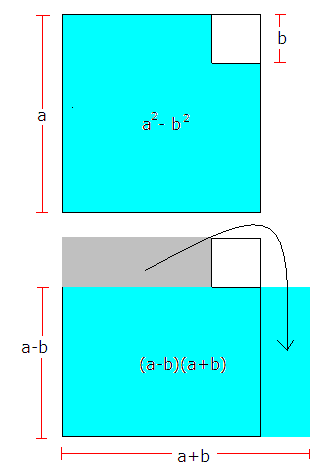
Konjugatsetningen

<tex>(a + b)(a - b) = a^2 - b^2 </tex>

<tex>(5 + 2x)(5 - 2x) = 5^2 - 10x + 10x - 4x^2 = 25-4x^2 </tex>

<tex>9x^2 - 36y^2 = (3x+6y)(3x-6y) </tex>

Test deg selv

Forkorting av brøkuttrykk

Eksempel:
<tex> \frac {a^2}{ab}=\frac {a \cdot a }{a \cdot b} = \frac ab</tex>

<tex> \frac {a^2}{a^3}</tex>

<tex> \frac {b}{b}</tex>

<tex> \frac {(x+2)(x-2)}{(x+2)x}= \frac {(x+2)(x-2)}{(x+2)x}=</tex>

<tex> \frac {x^2 - 6x + 9}{2x^2 - 18}= \frac {(x-3)^2}{2(x+3)(x-3)}=</tex>

@@ Linje 196: / Linje 196: @@
-Nr. (6) er andre kvadratsetning og nr. (5) er første kvadratsetning som også er illustrert grafisk nedenfor.
-Disse syv setningene bør du lære deg utenat, begge veier. Årsaken til det er at du er avhengig av å gjenkjenne utrykk som en eller flere av disse sammenhengene.
-Eksempler
-Fra tallregningen er vi vant med at svaret blir et tall bestående av et eller flere siffer. Det ser veldig pent ut.
-I algebra blir gjerne svaret flere bokstaver, ledd, produkter og brøk. Dette er helt ok. og Ikke noe å bekymre seg over.
-Eksempel 2:
-Forkort uttrykket:
-Vi ser at (x-1) er en faktor i både teller og nevner, derfor kan vi forkorte den bort. Det blir imidlertid stående en igjen. Det er bare når vi har faktorer at vi kan forkorte. Dersom vi har et ledd kan vi ikke forkorte, selv om leddet er en del av en faktor. (Vi kan selvfølgelig forkorte hele faktoren dersom det er mulig.)
-Hvilket av de to svarene vi velger avhenger av smak og behag og hva vi skal bruke resultatet til. Begge bør bli godtatt.
-Eksempel 3:
-Skriv enklest mulig:
-Husk at når du forkorter blir det alltid en igjen. Selv om vi har forkortet bort tre u'er i teller og nevner står vi fortsatt igjen med en i teller
-Eksempel 4:
-Skriv enklest mulig:
-Av og til må man bare akseptere at utrykket ikke kan forkortes. Da er det bare å sette to streker under svaret. Det kunne jo være fristende å prøve å forkorte a'ene, men det er ikke mulig da a'ene i teller ikke er en faktor, men et ledd.
-Eksempel 5:
-Skriv enklest mulig:
-Vi skal prøv å forenkle utrykket. Det ser jo ikke spesielt lovende ut her.. Vel, hovedregelen når vi skal forenkle brøkuttrykk er å tenke faktorisering. Vi ser at telleren er andre kvadratsetning og kan skrives som (w - 3)(w - 3). I nevner ser vi at tallet to kan settes utenfor en parentes. Utrykket i parentesen gjenkjenner vi som konjugatsetningen. Vi får:
-Eksempel 6:
-Trekk sammen og skriv enklest mulig:
-Regelen er at vi multipliserer ut alle parentesene først. Deretter samler vi andregradsleddene for seg, førstegradsleddene for seg og tallene for seg. Dette er enkelt nok, men tidkrevende. Vær forsiktig, det er lett å gjøre fortegnsfeil her!
-Eksempel 7:
-Skriv enklest mulig:
-Først finner vi fellesnevner. Sett utrykket på felles brøkstrek. Multipliser ut i teller og trekk sammen. La nevner stå faktorisert. Når teller er regnet ut faktoriseres den. Forkort det som er mulig, i dette tilfellet 2•2.
 [[Kategori:Algebra]] [[Kategori:1T]][[Kategori:2P]]