S1 2019 høst LØSNING

Diskusjon av denne oppgaven på matteprat

Løsningsforslag laget av Svein Arneson

Løsningsforslag del 1 laget av Emilga

Løsningsforslag del 2 laget av Kristian Saug

Oppgaven som pdf

DEL 1

Oppgave 1)

a)

$x^2+4x-12=0 \\ (x-2)(x+6)=0 \\ x=-6 \vee x=2$

b)

$lg(5-2x)=1 \\ 5-2x =10 \\ -2x = 5 \\ x= -\frac{5}{2}$

Oppgave 2)

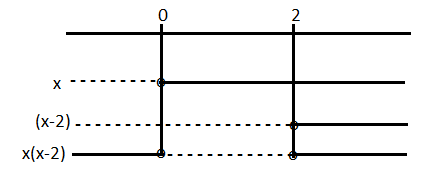
$x^2-2x<0$

Finner nullpunktene.

$x(x-2)=0 \\ x=0 \vee x=2$

$x^2-2x<0$ når $0<x<2$

Oppgave 3)

$x^2+4y=4x \\ 4x-2y=6$

Ganger likning II med 2 og bruker addisjonsmetoden.

Likning II ganger 2:

$8x-4y=12$

Legger sammen likningene:

$x^2+4y+8x-4y=4x+12 \\ x^2+4x-12=0 \\ x_1=-6 \vee x_2=2$

(Samme likning som i oppgave 1a)

Gjør om likning II:

$4x-2y=6 \\ -2y=6-4x \\ y=-3+2x$

Setter inn de to x-verdiene:

$y_1=-3 + 2\cdot (-6) = -15$

$y_2=-3+2\cdot 2=1$

Løsninger:

$x_1=-6, y_1=-15 \\ x_2=2, y_2=1 $

Oppgave 4)

a)

$(a+2)^3-a\cdot(a+2)^2 \\ =(a+2)(a+2)^2-a\cdot(a+2)^2 \\ =(a+2)^2\cdot((a+2)-a) \\ =(a^2+4a+4)\cdot 2 \\ =2a^2+8a+8$

b)

$\frac{x+1}{x+2}-\frac{x+1}{x-1}-\frac{x+5}{x^2+x-2}$

$=\frac{(x+1)(x-1)}{(x+2)(x-1)}-\frac{(x+1)(x+2)}{(x-1)(x+2)}-\frac{x+5}{(x+2)(x-1)}$

$=\frac{x^2-1}{(x+2)(x-1)}-\frac{x^2+3x+2}{(x-1)(x+2)}-\frac{x+5}{(x+2)(x-1)}$

$=\frac{(x^2-1)-(x^2+3x+2)-(x+5)}{(x+2)(x-1)}$

$=\frac{x^2-1-x^2-3x-2-x-5}{(x+2)(x-1)}$

$=\frac{-4x-8}{(x+2)(x-1)}$

$=\frac{-4(x+2)}{(x+2)(x-1)}$

$=\frac{-4}{x-1}=\frac{4}{1-x}$

c)

$2lg(2x^2)+lg\frac{5}{x}-lg(2x^3)$

$2lg2+2lg(x^2)+lg5-lgx-(lg2+lg(x^3))$

$2lg2 + 4lgx + lg5 - lg x -lg 2 - 3lg x$

$lg 2 + lg 5 = lg (2\cdot5) = lg 10 = 1$