2P 2019 høst LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsning del 2 laget av mattepratbruker Kristian Saug

Oppgave 1

1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 8

a)

Median er gjennomsnittet av de to tallene i midten av tallmaterialet ( tall 10 og 11) som er $\frac {3+4}{2} = 3,5$

Gjennomsnittet er summen av alle observasjoner, delt på antallet observasjoner, altså:

$\frac{1+ 1+ 2+ 2+ 2+ 3+ 3+ 3+ 3+ 3+ 4+ 4+ 4+ 4+ 5+ 5+ 5+ 6+ 6+ 8}{20} = \frac{74}{20} = 3,7$

b)

Den kumulative frekvensen for 3 betyr hvor ofte 3 eller mindre forekommer i datamaterialet. Altså 1,1,,2,2,2 og 3,3,3,3,3 som til sammen er 10 forekomster. Den kumulative frekvensen for 3 er ti.

På norsk betyr det at 10 av de 20 spurte bruker tre eller mindre enn tre timer foran en skjerm hver dag.

Den relative frekvensen er hvor stor del noe utgjør av helheten. Det var fem som svarte 3 timer, av tyve spurte. Den relative frekvensen for 3 blir da $\frac {5}{20} = 0,25$ Man oppgir oftest relativ frekvens som et desimaltall, eller prosentfaktor. 0,25 tilsvarer 25%.

Oppgave 2

Dersom 15 stk er hvite og 40% er røde, vet vi at 60% tilsvarer 15 stk. Da er 20% lik 5 stk. 40% er da 10 stk.

$ \frac{15 \cdot 40}{60} = 10$

Vi deler 15 på 60 som gir en prosent, multipliserer med 40 for å finne hvor mange 40% er. Det er altså 10 stk.

Oppgave 3

$\frac{1,2 \cdot 10^7 - 6,5 \cdot 10^6}{0,0005} = \\ \frac{(12-6,5) 10^6}{5 \cdot 10^{-4}} = \\ \frac{5,5}{5} \cdot 10^{6 - (-4)} = \\ 1,1 \cdot 10^{10} $

Eller slik:

$\frac{1,2 \cdot 10^7 - 6,5 \cdot 10^6}{0,0005} = \\ \frac{12 000 000-6 500 000}{5 \cdot 10^{-4}} = \\ \frac{5 500 000}{ 5} \cdot 10^4 = \\ 1 100 000 \cdot 10^4 = 1,1 \cdot 10^{10}$

Oppgave 4

Vi omformer tallene slik at det blir lettere å sammenligne dem:

$ 75^0 = 1 \\ 2^3 \cdot 2^2 = 32 \\ (2^3)^2 = 64 \\ 2^{-3} = \frac 18 \\ \frac{1}{4^2} = \frac {1}{16}$

Vi får da følgende rekkefølge :

$ \frac {1}{4^2}, 2^{-3}, 75^0, 2^3 \cdot 2^2, (2^3)^2$

Oppgave 5

a)

L (x )= 40x + 60

L er lønna, som er avhengig av x

x er antall produkter

40 er beløpet hun får for hvert produkt (x) hun selger.

60 er fastlønna, uavhengig av x.

Denne funksjonen er en rett linje med 60 som konstantledd og 40 som stigningstall.

b)

$L(x) > 200 \\ 40x+60 >200 \\ 40x >200 - 60 \\ 40x > 140 \\ x > \frac{140}{40} x > 3,5 $

Hun må selge fire produkt i timen for å få en timelønn over 200kr.

c)

Vi sjekker hvor mange produkter hun må selge for at tilbudene gir samme lønn.

$40x + 110 = 48x +60 \\ - 8x = - 50 \\ x = 8,25$

Dersom hun vanligvis, mesteparten av tiden, selger åtte produkter eller mindre, lønner det seg å ta tilbudet med økt fastlønn. Selger hun vanligvis 9 eller flere er alternativ to best.

Oppgave 7

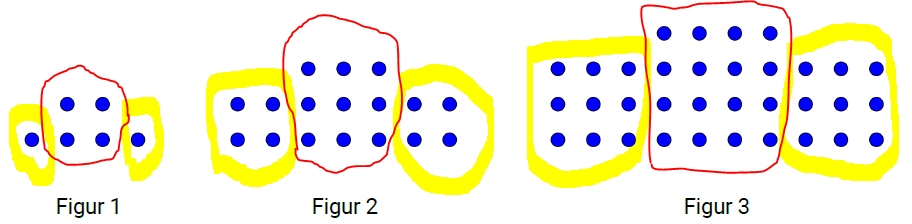
Vi legger merke til at alle figurene kan deles i tre. De to gule delene er like. I figur 2 er antallet sirkler $2^2$ i en gul del, og $3^2$ i figur 3.

a)

Fra figuren over ser man at figur nr. 4 vil bestå av fire ganger fire, pluss fem ganger fem, pluss fire ganger fire antall kuler:

$4^2 + 5^2 + 4^2 = 16 + 25 + 16 = 57$

Det er 57 kuler i figur 4.

b)

Vi ser at de to "gule" kvadratene har sidekanter med samme antall kuler som figurnummer, mens det "røde" kvadratet i midten har en kule mer i sidekanten enn figurnummeret.

Kaller antall kuler for A(n)

Vi får da:

$A(n) = n^2 + (n+1)^2 + n^2 = 2n^2 + (n+1)^2 = 2n^2+n^2+2n+1 = 3n^2+2n+1$

c)

Figur nr. 100:

$A(100) = 3 \cdot 100^2 + 2 \cdot 100 + 1 = 30000 + 200 + 1 = 30201 $