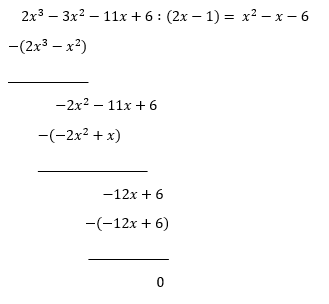R1 2019 vår LØSNING

Oppgaven som pdf

Løsningsforslag laget av matteprat-bruker SveinR

Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas

Diskusjon av denne oppgaven på matteprat

DEL 1

Oppgave 1

a)

$f(x)=x^3+2x^2-\sqrt{x} \\ f'(x)=3x^2+4x-\frac{1}{2\sqrt{x}}$

b)

$g(x)=x^2\cdot ln(2x-1) \\ g'(x)=2x\cdot ln(2x-1)+\frac{2x^2}{2x-1}$

Brukte produktregelen og kjerneregelen. Løsningen kan evt. faktoriseres.

c)

$ h(x) = \frac{4x}{e^{2x}} \\ h'(x)=\frac{4e^{2x}-4x\cdot 2e^{2x}}{(e^{2x})^2} \\ = \frac{e^{2x}(4-8x)}{(e^{2x})(e^{2x})} = \frac{-8x+4}{e^{2x}}$

Oppgave 2

a)

$\frac{1}{x^2-x}+\frac{1}{x^2+x}-\frac{1}{x^2-1} \\ = \frac{1}{x(x-1)}+\frac{1}{x(x+1)}-\frac{1}{(x+1)(x-1)} \\ = \frac{x+1}{x(x-1)(x+1)}+\frac{x-1}{x(x+1)(x-1)}-\frac{x}{x(x+1)(x-1)}\\ = \frac{x+1+x-1-x}{x(x+1)(x-1)} \\ = \frac{x}{x(x+1)(x-1)} \\ = \frac{1}{x^2-1}$

b)

$\frac{(ln\,e^3+1)^2}{(e^{ln\,3}+1)} = \frac{(3+1)^2}{(3+1)^3}=\frac{4^2}{4^3}=\frac{1}{4}$

Oppgave 3

a)

$(2x-1)=0 \\ x=\frac{1}{2}$

Sjekker om $x=\frac{1}{2}$ er et nullpunkt for $f(x)$:

$f(\frac{1}{2})= 2(\frac{1}{2})^3-3(\frac{1}{2})^2-11\cdot \frac{1}{2}+6 \\ = \frac{2}{8}-\frac{3}{4}-\frac{11}{2}+6 \\ = \frac{2}{8}-\frac{6}{8}-\frac{44}{8}+6 \\ = \frac{-48}{8}+6 = -6+6 = 0$

$x=\frac{1}{2}$ er et nullpunkt for $f(x)$, det vil si at divisjonen $f(x):(2x-1)$ går opp.

b)

Utfører polynomdivisjonen $f(x) : (2x-1)$

$x^2-x-6=(x-3)(x+2)$

$f(x)=(2x-1)(x-3)(x+2)$

c)

$f(x) \geq (2x-1)(x+2) \\ (x-3)(2x-1)(x+2) \geq (2x-1)(x+2) \\ (x-3)(2x-1)(x+2) - (2x-1)(x+2) \geq 0$

Setter felles faktor $(2x-1)(x+2)$ utenfor parentes.

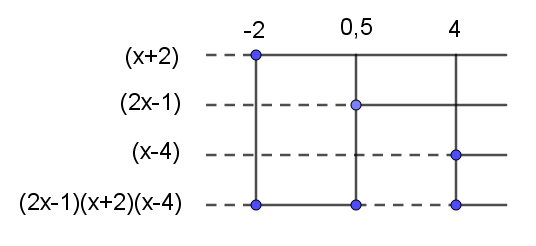
$ (2x-1)(x+2)((x-3)-1) \geq 0 \\ (2x-1)(x+2)(x-4) \geq 0 $

$f(x) \geq (2x-1)(x+2)$ når $x \in [-2, \frac{1}{2}] \cup [4,\infty \rangle$