1P 2016 høst LØSNING: Forskjell mellom sideversjoner
| Linje 235: | Linje 235: | ||
===c)=== | ===c)=== | ||
Tidsperioden er 20 år. Veksten ansløes til å være ca. 33 kg i denne perioden, dvs en økning på 1,65 kg per år. I 1954 er forbruket ca 41 kg. Vi får da: | |||
y= 1,65x + 41 | |||
==Oppgave 8== | ==Oppgave 8== | ||
Sideversjonen fra 22. des. 2016 kl. 09:57
Diskusjon av denne oppgaven på matteprat
Mer diskusjon av denne oppgaven på matteprat
DEL EN
Oppgave 1
$8: \frac 23 = \frac{8 \cdot 3}{2} = 12$
Jeg trenger 12 bokser.
Oppgave 2
$\frac{5cm}{1,5km} = \frac 1x \\ \Downarrow \\ \frac{5cm}{150000cm } = \frac 1x \\ \Downarrow \\ x= \frac{150000}{5} = 30000$
Målestokken på kartet er 1: 30 000.
Oppgave 3
$\frac 25 = \frac6x \\ 2x=30 \\ x=15$
Det ligger 15 basketbaler i kassen,tilsammen 21baller.
Oppgave 4
a)
$\frac 15 = \frac {2}{10} = \frac{20}{ 100} = 20$ %
$\frac{135}{250} = \frac{540}{1000} = \frac{54}{100} = 54$ %
b)
$\frac 15 \cdot \frac 34 = \frac {3}{20} = \frac{15}{100} = 15$ %
Det er 15% av elevene som spiller håndball.
Oppgave 5
a)
$kroneverdi = \frac{100}{KPI}$
Når KPI øker blir kroneverdien mindre. Kroneverdi multiplisert med KPI er alltid 100.
b)
Oppgave 6
$ AB = \sqrt{7,0^2 + 6,0^2} = \sqrt{85}$
Siden kvadratroten av 81 er 9 vil lengden AB være noe lengre enn 9,0 meter.
Oppgave 7
a)
$y=kx \Rightarrow k = \frac yx = \frac{350 kr}{50 kg} = \frac{700 kr}{100 kg} = \frac{1750kr}{250kg} = \frac{2800kr}{400kg} = 7 $ kr/kg
b)
Pris: y (kroner)
Mengde x (kilogram)
y=7x
Oppgave 8
Omrets av figur : $O= 2AB + 2BC + \pi \cdot r \\ O \approx 20 + 24 + 3 \cdot 6 \\O \approx 62 $
Høyen fra BE til A: $ h = \sqrt{100 - 36} = 8$
Areal av figur: $A = \frac 12 \cdot BC \cdot h + BC \cdot BE + \frac{\pi \cdot r^2}{2} \\ A \approx 0,5 \cdot 12 \cdot 8 + 12 \cdot 12 + \frac{3 \cdot 6^2}{2} \\ A \approx 48 + 144 + 54 \\ A \approx 246 $
Oppgave 9
a)
$K(x)= x^2+ b \cdot x +20000 \\ K(0) = 20000$
Det betyr at de faste kostnadene er 20000 kroner. Altså kostnader før man har produsert en eneste enhet.
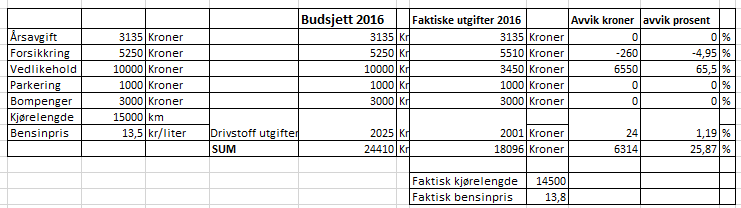
b)
$30000 = 50^2 + 50b + 20000 \\ 50b = 30000 - 20000 - 2500 \\ 50b = 7500 \\ b= 150$
Oppgave 10
a)
$P(BRR) = \frac{4}{8} \cdot \frac{4}{7} \cdot \frac{3}{6} = \frac 17$
b)
Det er tre possisjoner for blå nisse: P( en blå og to røde)$ = 3 \cdot \frac 17 = \frac 37$
c)
Dersom vi IKKE har minst en blå har vi tre røde. Sannsynliheten for det er:
P( bare røde)=$ \frac 48 \cdot \frac 37 \cdot \frac 26 = \frac{1}{14}$
Sannsynligheten for minst en blå blir da:
P( minst en rød) = $1- \frac{1}{14} = \frac{13}{14}$
Oppgave 11
a)
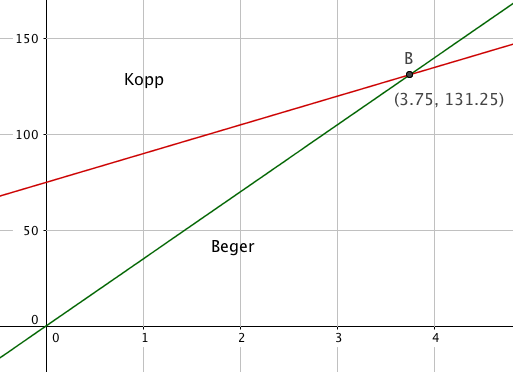
$f(x)= 35x$
b)
g(x)= 90 + 15(x-1) = 15x + 75
c)
$f(x) = g(x) \\ 35x = 15x + 75 \\ 20x = 75 \\ x = 3,75$
Ved kjøp av fire drikke vil det lønne seg å kjøpe kopp.
DEL TO
Oppgave 1
a)
b)
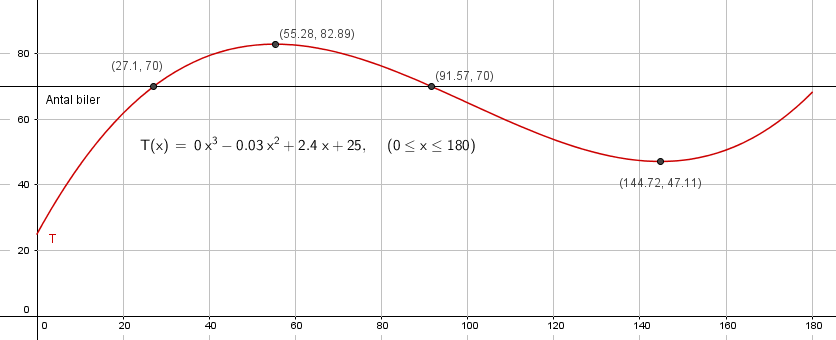
Fra figuren i a ser man at klokka 06:55 passerer det ca 83 biler per minutt.
c)
Fra figuren i a ser man at det passerer mere enn 70 biler per minutt i tidsrommet 06:27 til 07:32.
Oppgave 2
a)
Vinkel B er lik vinkel E.
Vinkel C i begge er like fordi de er toppvinkler. Da er vinkel A lik vinkel D og trekantene er formlike.
b)
Forholdet mellom sidene i ABC og CDE er $\frac{74,2}{53} = 1,4$
BC: $\frac{28}{x} =1,4 \\ x = \frac{28}{1,4} = 20$
Lengden av BC er 20.
AB: $(74,2)^2 = (AB)^2 + (20)^2 \\ AB = \sqrt{5505,64 - 400}\\ AB = 71,45$
c)
Forhold mellom areal:
Forholdet mellom sidene i trekantene er 1,4 og arealet av en trekant er $A= \frac 12 gh$
$\frac{A_{stor}}{A_{liten}} = (1,4)^2 = 1,96$
Den store trekanten har 1,96 ganger så stort areal som den lille.
Oppgave 3
Dersom reallønnen er uendret er kjøpekraften opprettholdt.
$ Reallønn = lønn \cdot \frac{100}{KPI} \\ 520800 \cdot \frac{100}{139,8} = 375532$
Dersom reallønnen i 2016 er 375 532 kroner er kjøpekraften opprettholdt.
Oppgave 4
$850000 \cdot 0,800 \cdot 0,965^5 = 569043,5$
Etter seks år har båten en verdi på ca, 570 000 kroner.
Oppgave 5
a)
Overflate kiste:
Bunn $ 0,41m \cdot 0,95 m = 0,3895m^2 $
Forside og bakside: $2 \cdot 0,95m \cdot 0,62 m = 1,178 m^2$
Sidekanter: $2 \cdot 0,41m \cdot 0,62m = 0,5082m^2$
Lokk:
b)
Oppgave 6
a)
b og c)
Oppgave 7
a)
Økningen var fra ca. 40 kg i 1970 til ca 60 kg i 2000. En økning på 20 kg, $\frac {20}{40} = 0,50$. Økningen var på ca 50 %.
b)
I denne perioden har grafen form som en rett linje, altså lineær vekst.
c)
Tidsperioden er 20 år. Veksten ansløes til å være ca. 33 kg i denne perioden, dvs en økning på 1,65 kg per år. I 1954 er forbruket ca 41 kg. Vi får da:
y= 1,65x + 41
Oppgave 8
a)
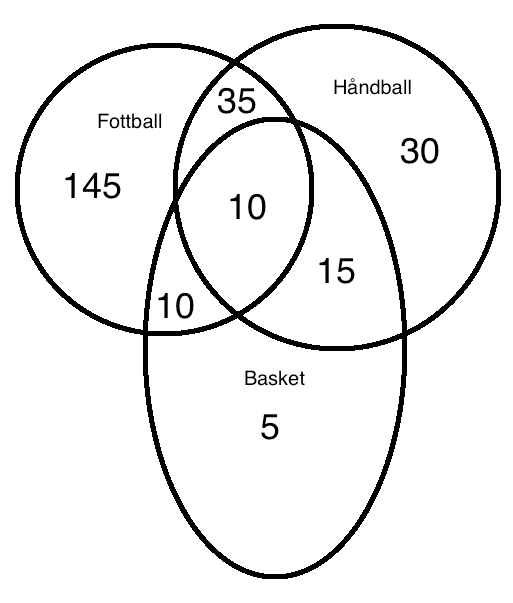
Basketball og håndball er: 90 - 30 - 35 - 10 = 15
160 medlemmer spiller bare fotball og / eller basketball. Det betyr at 10 gjør begge deler:
b)
$ P( F \cap H \cap B) = \frac{10}{250} = \frac {1}{25}= $ 4%
Det er fire prosent sannsynlighet for å velge en som driver med alle tre idrettene.
c)
$P(F| H) = \frac{45}{90} = \frac 12$
Det er 50% sannsynlighet for at en som driver med håndball også spiller fotball.
Oppgave 9
Vi ser at dersom 12 går sammen må hver betale 1000 kroner. Trampolina koster 12000 kroner.
12 000 kr : 25 = 480 kroner.
Dersom 25 går sammen må hver av dem betale 480 kroner.