Modellering: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| Linje 14: | Linje 14: | ||
===Korrelasjonskoeffesienten=== | ===Korrelasjonskoeffesienten=== | ||
Korrelasjonskoeffesienten er en statistisk størrelse som brukes for å måle korrespondansen mellom parametre og målinger. Den avhenger kun av datapunktene, ikke av kurvene, og er derfor ikke egnet til å bedømme om kurver er gode tilpasninger. Til det brukes metoden med minste | Korrelasjonskoeffesienten er en statistisk størrelse som brukes for å måle korrespondansen mellom parametre og målinger. Den avhenger kun av datapunktene, ikke av kurvene, og er derfor ikke egnet til å bedømme om kurver er gode tilpasninger. Til det brukes metoden med minste kvadratavvik. | ||
===Minste | ===Minste kvadratavvik=== | ||
[[Bilde:Reg1.png]] [[Bilde:Reg2.png]] | [[Bilde:Reg1.png]] [[Bilde:Reg2.png]] | ||
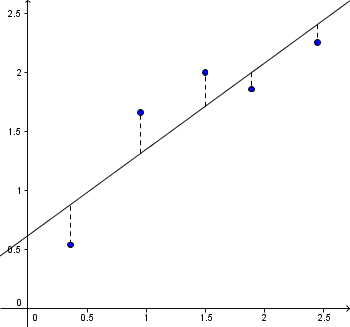
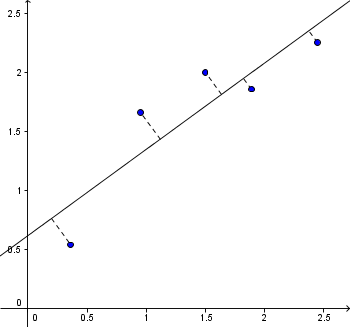
Minste | Minste kvadratavvik er den mest brukte metoden for tilpasning av kurver. Det finnes to måter å gjøre dette på; vertikalt avvik (venstre figur over) og vinkelrett avvik (høyre figur over). På grunn av de kompliserte algoritmene som må tas i bruk på sistnevnte, er det minste kvadratavvik med vertikalt avvik som er mest brukt. | ||
Denne består av at man har en mengde målepunkter på formen <tex>P_i(x_i,y_i)</tex>, og at man fnner funksjonen <tex>y=f(x)</tex> slik at | Denne består av at man har en mengde målepunkter på formen <tex>P_i(x_i,y_i)</tex>, og at man fnner funksjonen <tex>y=f(x)</tex> slik at | ||
Sideversjonen fra 28. jan. 2010 kl. 14:29
Modellering er en del av statistisk analyse der man fra en mengde målepunkter prøver å finne en matematisk sammenheng mellom variabler (parametre) og målinger.
Når man lager modeller har man i mange tilfeller bruk for et grafisk hjelpemiddel som kan gjøre grovarbeidet. Til dette brukes vanligvis grafiske kalkulatorer på skolen. Et gratis alternativ er Geogebra.
Statistisk modellering har anvendelser i mange praktiske fag, som fysikk, kjemi, økonomi og ingeniørfag.
Hovedfokuset i fagene i videregående skole er å fra målepunktene kunne virdere hvilken type funksjon som best vil beskrive sammenhengen mellom parametre og målinger.
Teknikker for modellering
Algoritmene som brukes i tilpasningen av kuver til datapunkter er ofte så lange og omfattende at kun datamaskiner brukes. Det er likevel lurt å være klar over kriteriene som brukes for å bedømme om en gitt kurve er en god tilpasning, og hvilken kurve blandt flere som best beskriver den.
Korrelasjonskoeffesienten
Korrelasjonskoeffesienten er en statistisk størrelse som brukes for å måle korrespondansen mellom parametre og målinger. Den avhenger kun av datapunktene, ikke av kurvene, og er derfor ikke egnet til å bedømme om kurver er gode tilpasninger. Til det brukes metoden med minste kvadratavvik.
Minste kvadratavvik
Minste kvadratavvik er den mest brukte metoden for tilpasning av kurver. Det finnes to måter å gjøre dette på; vertikalt avvik (venstre figur over) og vinkelrett avvik (høyre figur over). På grunn av de kompliserte algoritmene som må tas i bruk på sistnevnte, er det minste kvadratavvik med vertikalt avvik som er mest brukt.
Denne består av at man har en mengde målepunkter på formen <tex>P_i(x_i,y_i)</tex>, og at man fnner funksjonen <tex>y=f(x)</tex> slik at
<tex>\sum_{i} \left( f(x_i)-y_i \right) ^2</tex>
, der stor sigma står for sum over <tex>i</tex>, minimeres.
- Vertikalt kvadratavvik i Geogebra
- I den nyeste versjonen av Geogebra (Se lenke øverst på siden) er det mulig å beregne det kvadratavviket mellom en funksjon og en mengde målepunkter. Dette gjøres i følgende steg:
- 1. Lag en mengde med målepunkter. Dette gjøres ved å legge ut målepunktene i vinduet og legge disse i en liste. Hvis du har målepunktene A-F, for eksempel, lages listen ved å skrive
L={A,B,C,D,E,F}
- i kommandolinjen.
- 2. Lag funksjonen enten ved å skrive inn et funksjonsuttrykk i kommandolinjen eller ved å utføre en regresjon med målepunktene. Regresjon på målepunkter viser vi lenger nede i artikkelen.
- 3. Nå som du har en liste L med målepunkter og en funksjon f(x), kan vi finne kvadratavviket ved å skrive i kommandolinjen:
- Nå vil Geogebra holde styr på kvadratavviket selv om du flytter på målepunktene eller endrer funksjonsuttrykk på funksjonen.
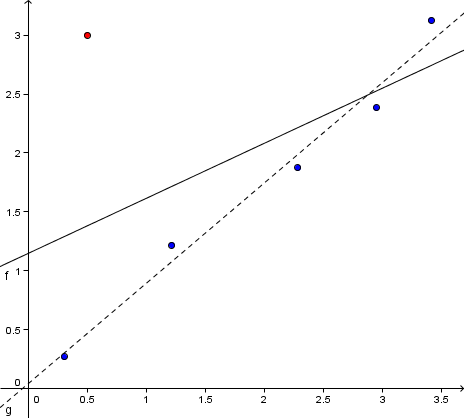
Avvikende målepunkter
Lineær modellering
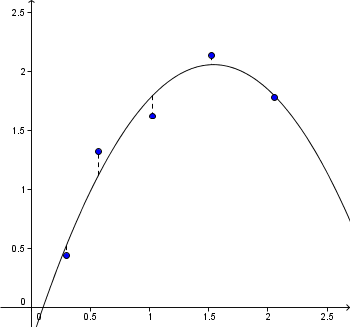
Ikke-lineær modellering
Polynomisk modellering
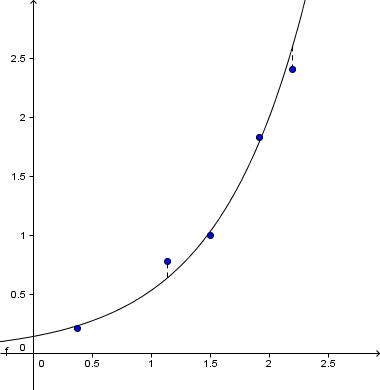
Eksponentiell modellering
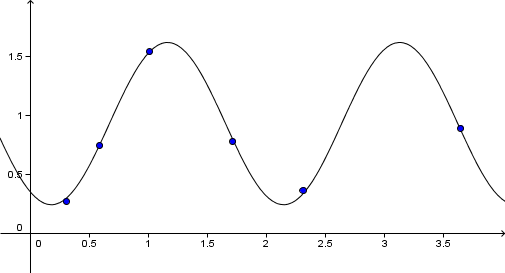
Sinusoidal modellering