2P 2016 vår LØSNING

Diskusjon av denne oppgaven på matteprat

Del 1 Løsningsforslag laget av mattepratbruker jøgge

Del 2 Løsningsforslag laget av mattepratbruker jøgge

Løsningsforslag fra mattepratbruker Oyan

DEL EN

Oppgave 1)

-6, -4, 0, 2, 2, 6.

Variasjonsbredde: 6 - ( - 6 ) = 12

Variasjonsbredden er 12 grader.

Median: $\frac {0+2}{2} = 1$

Median er 1 grad.

Gjennomsnitt: $\frac{-6 +(-4)+0+2+2+6}{6} = \frac 06 =0$

Gjennomsnittsteperaturen denne perioden er null grader celsius.

Oppgave 2)

Forutsetter at en måned er 30 dager.

$7500 000 000 \cdot 2 \cdot 30 = \\ 7,5 \cdot 10^9 \cdot 6,0 \cdot 10 = \\7,5 \cdot 6,0 \cdot 10^{10} = \\ 45 \cdot 10^{10} = 4,5 \cdot 10^{11}$

Oppgave 3)

Ptis bukse i butikk A: 150 kr, og i butikk B: 120 kr.

a)

$\frac{150-120}{120} = \frac 14 = 25$%

Buksene er 25% dyrere i butikk A, i forhold til i butikk B.

b)

$\frac{150-120}{150} = \frac 15 = 20$%

Buksene er 20% billigere i butikk B, i forhold til i butikk A.

Oppgave 4)

Pris på jakke uten MVA:

$x \cdot 1,25 = 750 \\ x= \frac{750}{1,25} = 600$

Jakken koster 600 kroner uten MVA, altså er merverdiavgiften 150 kroner.

Oppgave 5)

a)

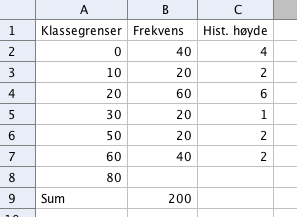
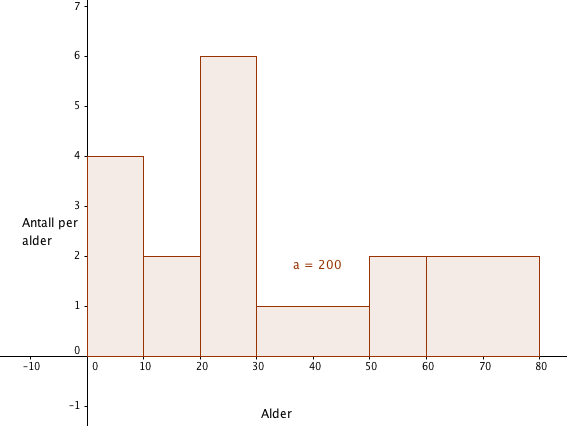
For å finn histogramhøyden tar man frekvens delt på klassebredde, for hver enkelt klasse.

b)

Gjennomsnitt i klassedelt materiale: vi antar at elementene i klassen (personer) fordeler seg jevnt utover i klassen. Kan da bruke klassemiddpunkt (alder) og multiplisere med frekvens.

Klasse	klassebredde - m	frekvens - f	m * f
[0,10>	5	40	200
[10, 20>	15	20	300
[20, 30>	25	60	1500
[30, 50>	40	20	800
[50, 60>	55	20	1100
[60, 80>	70	40	2800

For å finne gjennomsnittet tar man summen av alle produktene m*f og deler på antall personer som er 200.

$\frac{\sum(m \cdot f)}{200} = \frac{200 + 300 +1500 + 800 + 1100 + 2800}{200} = 33,5$

Gjennomsnittsalderen på beboerne i blokka er ca 33,5 år.

c)

Medianalderen er gjennomsnittet av person nr. 100 ig 101, når det er arrangert i stigende rekkefølge. Disse personene befinner seg i klassen 20 - 30 år. I denne klassen er det 6 personer på hvert årstrinn hvilket betyr at medianalderen er ca. 27 år. Aurora er ca. fem år eldre enn medianalderen, men kan jo trøste seg med at hun er yngre enn gjennomsnittet.

Oppgave 6)

a)

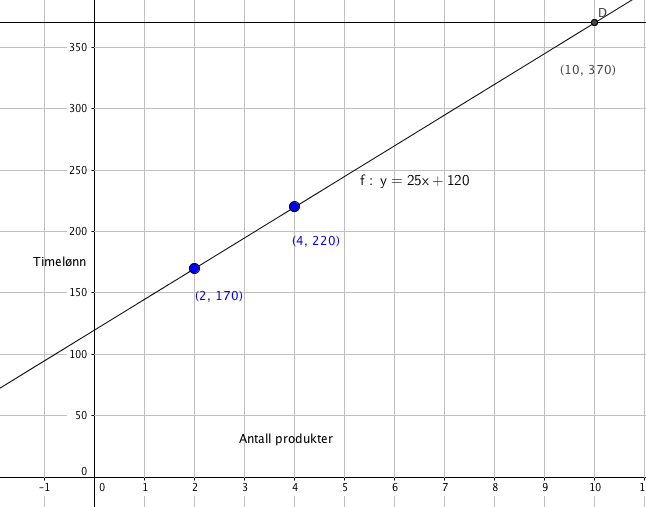
Vi plotter punktene i et koordinatsystem og trekker en rett linje. Denne linjen skjærer y aksen i 120, og stiger med 25 for hver enhet mot høyre på x-aksen.

y-aksen er timelønn og x-aksen er antall enheter.

b)

Den rette linjen i a har uttrykket y = 25x + 120.

Det betyr at fastlønna er 120 kroner og at hun i tillegg tjener 25 kroner for hvert produkt hun selger.

c)

Fra grafen i a ser man at hun må selge 10 produkter.

Oppgave 7)

a)

Dersom noe øker eksponentielt betyr det at det vokser med en fast prosent hver tidsperiode.

b)

b er eneste kurve som oppfuller kravet i a. c vokser lineært, altså med en fast størrelse hver tidsperiode. a vokser mindre etter en stund, noe som kan minne om logistisk vekst (ikke pensum i 2P).

Oppgave 8)

Skriver alle tallene på standardform:

$ 0,046\cdot 10^{11}= 4,6 \cdot 10^{9} \\ \frac{46}{1000000}= 0,000046 = 4,6 \cdot 10^{-5} \\ 46\cdot 10^{-7} =4,6 \cdot 10^{-6} \\ 4600000 = 4,6 \cdot 10^6 \\ 4,6 \cdot 10^8 \\ 0,46\cdot 10^{-6 } = 4,6 \cdot 10^{-7} $

Faktoren 4,6 går igjen i alle tallene og vi kan sortere etter størrelse ved å se på eksponenten i tierpotensen:

I stigende rekkefølge: $10^{-7}, 10^{-6}, 10^{-5}, 10^6, 10^8, 10^9.$

Oppgave 9)

Vi ser at kumulativ frekvens er 20 - altså 20 elever totalt.

Kummulativ frekv for 6-11 er 15, det betyr at frekvensen må være 10. Relativ frekvens er frekvensen delt på 20. "Nøster" vi opp slik får man følgende tabell:

Antall land	Frekvens	Relativ frekvens	Kumulativ frekvens
[1,6>	5	0,25	5
[6, 11>	10	0,5	15
[11, 16>	2	0,1	17
[16, 21>	2	0,1	19
[21, 26>	1	0,05	20

DEL TO

Oppgave 1

Oppgave 2

a)

Oppgave 4

a)

Figur	Ant. hvite rektangler	ant. blå rektangler	Ant. rektangler totalt
1	1	8	9
2	4	12	16
3	9	16	25
4	16	20	36
n	$n^2$	$4n + 4$	$n^2+4n+4$

b)

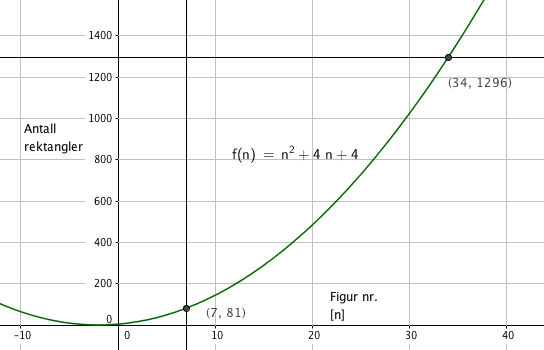
9 ganger 9 er 81, altså blir det figur nr 7 (n + 2) , det betyr at man trenger $7^2 = 49$ hvite rektangler.

c)

Bruker Figuren laget i Geogebra til å finne at det er snakk om figur nr 34. Antall blå rektangler blir da $4 \cdot 34 + 4= 140$

Oppgave 7

a)

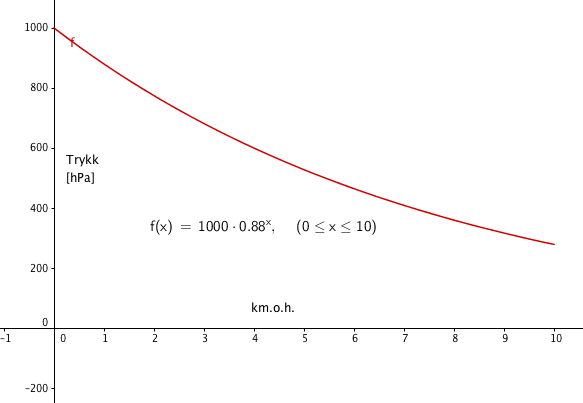
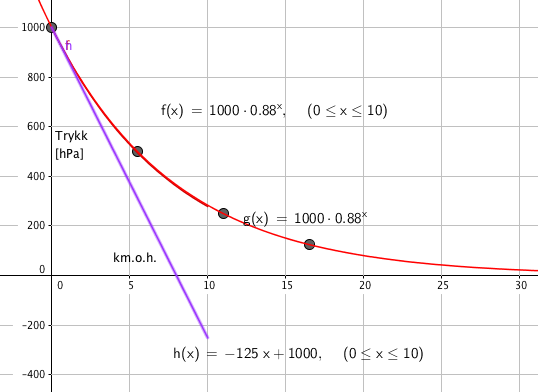
Siden trykket avtar med en fast prosent per km er dette eksponentiell vekst (om enn negativ) med vekstaktor 1 - 0,12 = 0,88. Desom vi i tillegg til sitat 1 inkluderer informasjone om lufttrykket ved havets overflate kan vi sette opp modellen:

$f(x) = 1000 \cdot 0,88^x$

Der x er kilometer over havets overflate.

b)

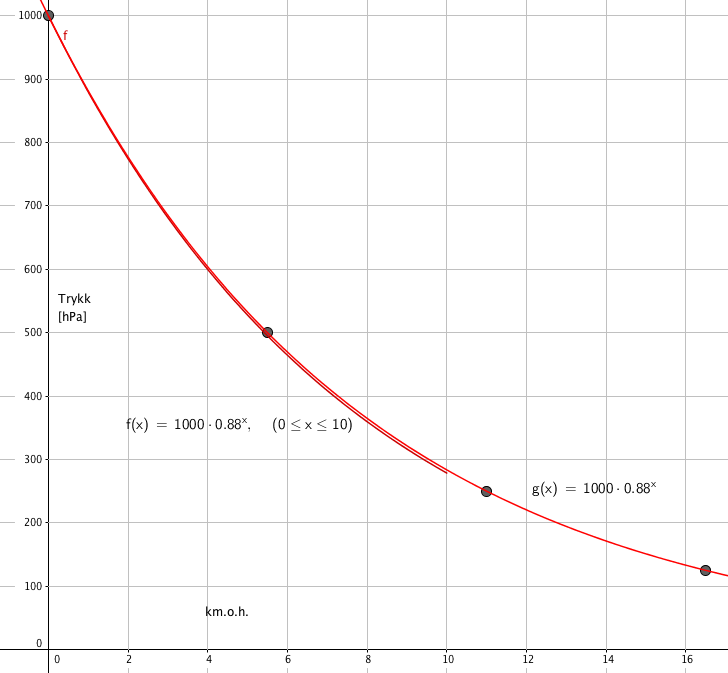
Lufttrykket halveres for hver 5,5 km opp fra havoverflaten

Vi observerer at den eksponentielle tilpassningen gir en modell praktisk talt lik den i a.

c)

Dette er en lineær modell som trolig virker bra til en hvis høyde over havet. Store høyder gir trolig store feil.

For å finne hvor mye trykket avtar per 1000 meter tar vi 1000:8 = 125 (hPa)

h(x)= -125x + 1000

Som vi antok er denne modellen kun gyldig i et lite begrenset område rett over havflaten.

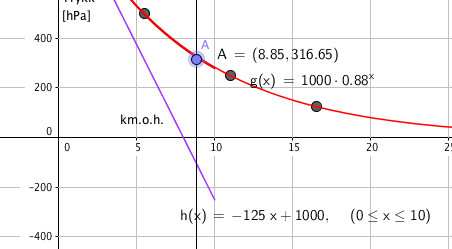
d)

Modell h er ubrukelig fordi høhden over havet er stor, den gir et negativt trykk??

Moddell f og g er i praksis like og gir et et rimelig svar, 317 hPa. Dersom sitat 4 skal tolkes som en absolutt sannhet underestimerere begg modellene marginalt. Man burde da fått 333,33 hPa.