2P 2016 vår LØSNING

Diskusjon av denne oppgaven på matteprat

Del 1 Løsningsforslag laget av mattepratbruker jøgge

Del 2 Løsningsforslag laget av mattepratbruker jøgge

Løsningsforslag fra mattepratbruker Oyan

DEL EN

Oppgave 1)

-6, -4, 0, 2, 2, 6.

Variasjonsbredde: 6 - ( - 6 ) = 12

Variasjonsbredden er 12 grader.

Median: $\frac {0+2}{2} = 1$

Median er 1 grad.

Gjennomsnitt: $\frac{-6 +(-4)+0+2+2+6}{6} = \frac 06 =0$

Gjennomsnittsteperaturen denne perioden er null grader celsius.

Oppgave 2)

Forutsetter at en måned er 30 dager.

$7500 000 000 \cdot 2 \cdot 30 = \\ 7,5 \cdot 10^9 \cdot 6,0 \cdot 10 = \\7,5 \cdot 6,0 \cdot 10^{10} = \\ 45 \cdot 10^{10} = 4,5 \cdot 10^{11}$

Oppgave 3)

Ptis bukse i butikk A: 150 kr, og i butikk B: 120 kr.

a)

$\frac{150-120}{120} = \frac 14 = 25$%

Buksene er 25% dyrere i butikk A, i forhold til i butikk B.

b)

$\frac{150-120}{150} = \frac 15 = 20$%

Buksene er 20% billigere i butikk B, i forhold til i butikk A.

Oppgave 4)

Pris på jakke uten MVA:

$x \cdot 1,25 = 750 \\ x= \frac{750}{1,25} = 600$

Jakken koster 600 kroner uten MVA, altså er merverdiavgiften 150 kroner.

Oppgave 6)

a)

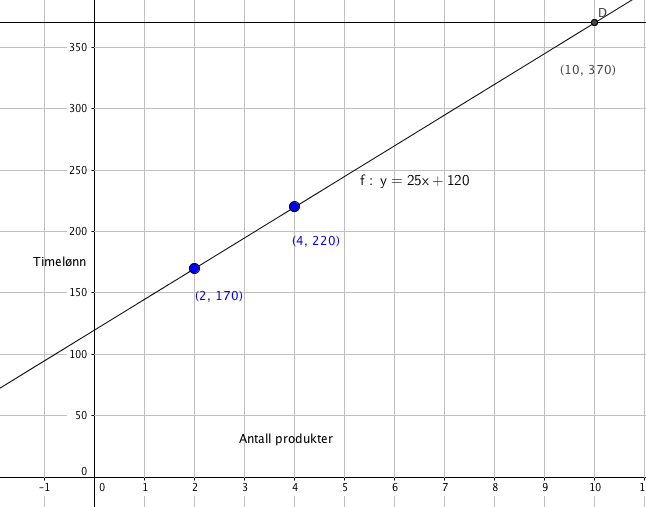
Vi plotter punktene i et koordinatsystem og trekker en rett linje. Denne linjen skjærer y aksen i 120, og stiger med 25 for hver enhet mot høyre på x-aksen.

y-aksen er timelønn og x-aksen er antall enheter.

b)

Den rette linjen i a har uttrykket y = 25x + 120.

Det betyr at fastlønna er 120 kroner og at hun i tillegg tjener 25 kroner for hvert produkt hun selger.

c)

Fra grafen i a ser man at hun må selge 10 produkter.

Oppgave 7)

a)

Dersom noe øker eksponentielt betyr det at det vokser med en fast prosent hver tidsperiode.

b)

b er eneste kurve som oppfuller kravet i a. c vokser lineært, altså med en fast størrelse hver tidsperiode. a vokser mindre etter en stund, noe som kan minne om logistisk vekst (ikke pensum i 2P).

Oppgave 8)

Skriver alle tallene på standardform:

$ 0,046\cdot 10^{11}= 4,6 \cdot 10^{9} \\ \frac{46}{1000000}= 0,000046 = 4,6 \cdot 10^{-5} \\ 46\cdot 10^{-7} =4,6 \cdot 10^{-6} \\ 4600000 = 4,6 \cdot 10^6 \\ 4,6 \cdot 10^8 \\ 0,46\cdot 10^{-6 } = 4,6 \cdot 10^{-7} $

Faktoren 4,6 går igjen i alle tallene og vi kan sortere etter størrelse ved å se på eksponenten i tierpotensen:

I stigende rekkefølge: $10^{-7}, 10^{-6}, 10^{-5}, 10^6, 10^8, 10^9.$