Logaritmer: Forskjell mellom sideversjoner
| Linje 40: | Linje 40: | ||
===Logaritmen av et produkt=== | ===Logaritmen av et produkt=== | ||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | <blockquote style="padding: 1em; border: 3px dotted blue;"> | ||
| Linje 47: | Linje 47: | ||
</blockquote> | </blockquote> | ||
<blockquote style="padding: 1em; border: 3px dotted red;"> | <blockquote style="padding: 1em; border: 3px dotted red;"> | ||
<tex> | <tex> log (10\cdot 100) = log 10 + log 100 = 1 + 2 = 3 </tex> | ||
10 ganger 100 er 1000. Logaritmen til 1000 er 3. Man ser at formelen stemmer. | |||
</blockquote> | </blockquote> | ||
Sideversjonen fra 26. jan. 2010 kl. 12:00
Bruk av logaritmer.
Logaritmeregningen ble introdusert av Napier rundt 1614, og arbeidet ble fullført av Briggs i 1628. Logaritmetabellene som de utviklet har vært i bruk helt fram til vår tid. Før kalkulatorer og regnemaskinenes tid spilte logaritmer en sentral rolle fordi de forenklet utregningen. Selv om man ikke er så avhengig av disse forenklingene i dag brukes logaritmer fortsatt, blant annet diagrammer der verdiene spenner over flere dekadiske enheter.
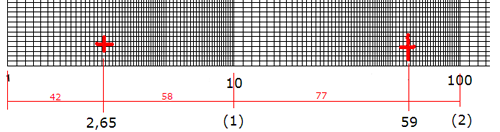
Nedenfor ser du del av et logaritmepapir. Man observerer at man har en fortetning av linjer mot høyre, når man nærmer seg 10, 100, osv. Det første punktet som er avmerket på papiret er 2,65. Logaritmen til 2,65 er 0,42, dvs. 100,42 = 2,65. Derfor ligger punktet 2,65 42 hundredeler fra 1 om man deler opp avstanden fra 1 til 10 i hundre like store deler. Tallene i parentes (1) 0g (2) er henholdsvis log10 og log 100.
Fig.1: Figuren viser del av et logaritmetapir over to sykler langs x - aksen, fra 1 - 10 og fra 10 - 100. Man kan få papir som spenner over 10 sykler hvilket muliggjør plotting over et spenn på 10 tierpotenser, for eksempel fra 0,0001 til 1.000.000. Legg merke til at hver gang en ny syklus starter øker faktoren med 10. Y - aksen på figuren er lineær. Man kan få logaritmepapir som er logaritmiske i begge retninger samtidig. Det markerte punktet til venstre i figuren markerer verdien 2,65. Det til høyre markere punktet 59.
Regneregler
Logaritmen til et tall x med basis b er definert som den inverse funksjonen til bx (b opphøyd i x).En logaritme kan ha forskjellige basiser eller grunntall (større enn null og ikke lik en). Det vanligste grunntallet for en logaritme er 10 og betegnelsen er log eller lg. Dersom andre grunntall brukes er det gjerne spesifisert, for eksempel dersom grunntallet er 2 skrives det slik: log2. Logaritmer med grunntall 10 kalles den briggske logaritmen , etter matematikeren Henry Briggs. Vi har følgende definisjon:
10log a= a
log 1000 = 3 fordi 103 = 1000
log 1 = 0 fordi 100 = 1
log 0,01 = -2 fordi 10-2 = 0,01
Logaritmen av en potens
<tex> log a^x = x \cdot log a</tex>
<tex> lol</tex>
Logaritmen av et produkt
<tex> log (a\cdot b) = log a + log b </tex>
<tex> log (10\cdot 100) = log 10 + log 100 = 1 + 2 = 3 </tex> 10 ganger 100 er 1000. Logaritmen til 1000 er 3. Man ser at formelen stemmer.
Logaritmen av en brøk
<tex> log \frac ab = log a - log b </tex>
<tex> lol</tex>
Endring av base (grunntall)
Det vanligste er å bruke 10 eller e som base, men et hvilket som helst tall kan i utgangspunktet brukes som base. Gitt en base b gjelder
<tex> b^{log_bx} = x </tex>
Ønsker så å skifte til base a:
<tex>log_a( b^{log_bx}) = log_a( x) </tex>
<tex>(log_bx) \cdot (log_a b)= log_a( x) </tex>
<tex>(log_bx) = \frac{log_a( x)}{ (log_a b) } </tex>
alle a, b og x er positive størrelser
I følge regnereglene for logaritmer får man da:
(lgbx)(lgab) = lgax
eller (i)
Du vil nok oppleve at de fleste kalkulatorer har problemer med andre baser enn 10 og e, men et enkelt eksempel illustrerer sammenhengen.
Eks 1:
3∙3∙3∙3 = 81, dvs. logaritmen til 81 er 4 dersom basen er 3, eller
lg381 = 4 som i følge formelen over skal være lik:
lg1081/lg103 = 4 som vi forventet ut fra (i).
Dersom man bytter alle x med a, i formel (i) får man:
I naturvitenskapen bruker vi ofte logaritmen til tallet e (e = 2,71828.....). Denne logaritmen kalles den naturlige logaritmen og brukes så ofte at den har fått en egen skrivemåte; ln. Vi har:
eln x= x
ln ax= x·ln a
ln (a·b) = ln a + ln b
ln a/b = ln a - ln b
Dersom du søker under derivasjonsregler vil du finne de som gjelder for ln og log.
Praktisk bruk
Surhetsgrad – pH
Et mol stoff er 6,022045· 1023 (avogadros tall) partikler. Mol per liter [M] brukes som et mål på konsentrasjon i væsker.
pH er definert som den negative logaritmen til konsentrasjonen av H+ (H 3O+) ioner i en løsning.
pH = - lg (H +)
pH 7 er nøytralt mens pH mindre enn 7 er surt. pH over 7 er basisk.
Dersom man bruker definisjonen finner man at
pH 14 = 0,00000000000001M = 1· 10-14 M
pH 7 = 0,0000001M = 1· 10 -7 M
pH 0 = 1,0 M = 1· 10 0 M
Eks. 1:
Konsentrasjonen av H + ioner i et avløp fra en bedrift måles over en periode på 3 år og gir følgende gjennomsnittsresultater:
1. år - 0,035 M
2. år - 0,00015 M
3. år - 0,000095 M
Nå kan man prøve å plotte resultatene direkte i et diagram, men man vil fort finne ut at man får problemer med skalaen fordi det er stor forskjell på observasjonene. Finner man pH de tre årene får man følgene resultater:
1. år - 0,035 M pH = - lg (0,035) = 1,5
2. år - 0,00015 M pH = - lg ( 0,00015) = 3,8
3. år - 0,000095 M pH = - lg (0,000095) = 4,0
Fig.2: Verdiene lar seg lettere plotte lineært når de er behandlet logaritmisk, i forhold til definisjonen for pH. Dersom du prøver å plotte konsentrasjonen direkte vil du få et problem med skalaen på aksene.
Eks.2:
Hva er konsentrasjonen av H+ ioner i en løsning der pH er 13?
13 = -lgC
c = 1∙ 10-13
Eks.3:
Hva er pH dersom konsentrasjonen av H+ i løsningen er 5,7 ∙10-9
pH = - lg(5,7 ∙10-9) = 8,2
Lyd - dB
Lyd
Lydstyrke måles I desibel, dB. Lyd er energi per flate og intensiteten på den svakeste lyden man kan høre er:
I0 = 10 -12 [W/m 2]
Dersom en lyd har intensiteten I er lydstyrken L, i desibel, gitt som
L = 10 lgI – 10 lg I0 = 10lgI + 120
Eks. 4:
Hva er lydintensiteten dersom lydstyrken er 60dB?
L = 10lgI + 120
lgI = (L-120)/10 = (60-120)/10 = -6
I = 10-6 = 0,000001 [W/m2]
Eks. 5:
Hva er lydstyrken dersom intensiteten er 3,7 ∙ 10-3[W/m2] ?
L = 10lg(3,7 ∙ 10-3) + 120 = 96dB
Eks. 6:
Hva skjer med lydstyrken når lydintensiteten dobles?
10lg(2I) +120=
10lg2 + 10lgI + 120=
10lgI +120 + 3 = L + 3
Når man dobler intensiteten øker lydstyrken med 3dB.
Som man ser fra eksemplene over er det mer praktisk å arbeide i dB, framfor å skulle arbeide direkte med lyditensitet.
Richters skala
Jordskjelv forårsakes av spenninger i jordskorpa. Sentrum av et jordskjelv kalles et episenter. Et jordskjelv friggjør energi i form av bølgebevegelser, som kan forårsake store materielle skader. Dersom episenteret er i eller ved vann kan det forårsake en stor flodbølger som kalles for en tsunami.
En av forskerne som arbeidet med matematiske modeller for å angi størrelsen på et jordskjelv var Dr. Charles F. Richter. Hen var Amerikaner og levde fra 1900 til 1985. I 1935 kom han med en modell som sier noe om styrken til et jordskjelv.:
E = 101,44R - 1,32
Der E er skjelvets energi målt i kWh og R er Richtertallet. Et jordskjelv som er 5 eller lavere på Richter skala er svakt og vil normalt ikke gi materielle skader. Jordskjelv over 6 på Richters skala er sterke. Skjelv over 8 vil normalt være katastrofale for store områder, flere hundre kilometer fra episentret. De største skjelv mann kjenner tilsvarer ca. 10 på Richters skala. Til sammenligning tilsvarer den daglige energimengden jorden mottar fra solen ca. 12 på Richters skala.
Eks. 7:
Hvor mye energi er utløst dersom et jordskjelv måler 7,9 på Richterskala?
E = 101,44∙7,9 - 1,32 = 1010,056=1,13 ∙ 1010 kWh
Eks. 8:
Et jordskjelv utløser en energimengde på 5 ∙ 106 kWh. Hvor stort er det på Richterskala?
5 ∙ 106 = 101,44R - 1,32
1,44R-1,32 =lg 5 ∙ 106
R = 5,6
logaritmepapir - plott
Nedenfor finner du linker til to sider der du kan skrive ut forskjellige typer logaritmepapirer, og mange andre typer papirer:
Avsnittene nedenfor vil gi deg en ide om hva slags papir du trenger.
Potensfunksjonen
Potensfunksjoner er funksjoner av typen:
y = axm
Ved å ta logaritmen på begge sider omformes uttrykket til en lineær funksjon.
lg y = lg a + m lg x
( husk at y = b + ax er ligningen for en rett linje)
Eks.9:
Vi ønsker å plotte funksjonen y = 5x1,6
Ved å velge lineære skala på begge akser får man:
Fig.3: Man observerer at grafen vokser raskt når x øker. Dette vanskeliggjør plotting over større intervaller av x og for store verdier av x.
Stigningstallet på et log-log papir finnes ved å ta
Man kan måle lengdene direkte på papiret fordi skalaen på begge akser er den samme. Generelt bør man måle over et størst mulig område for at nøyaktigheten skal bli tilfredsstillende.:
Stigningstallet er dy/dx =7,25/4,45 ≈ 1,6
Konstantleddet er 0,7 (lg 5) og finnes direkte ved å sette x=1, dvs. lg X = 0.
Det gir oss: lgy = lg 5 +1,6lgx
Som gir oss funksjonen vi startet med: y = 5x1,6 .
Eksponentsialfunksjonen
Eksponentsialfunksjoner er funksjoner av typen:
y = a·bx
Ved å ta logaritmen på begge sider av likhetstegnet får man:
lgy = lga + xlgb
Eks 10:
Vi ønsker å plott funksjonen y = 2,5(1,45)x
Fig 5: Man observerer at funksjonsverdien øker raskt når x vokser.
Fig.6: Ved å benytte logaritmisk skala på y aksen er det mulig å plotte grafen i et større intervall x verdier. Papiret i figuren spenner over seks sykler, fra 1 til 106
For å finne et uttrykk for y som funksjon av x velger man to punkter på grafen:
P1(5, 1,1) og P2(30, 5,15)
Vi tar utgangspunkt i y = abx
Vi setter inn verdiene for de to punktene og får
(I) 105,15 = ab30
(II) 101,1 = ab5
Ved å dividere ligningene på hverandre forsvinner a og man får
11220 = b25 dvs.
b ≈ 1,45
Innsatt (I) gir a ≈ 2 hvilket avviker fra riktig løsning som er 2,5 (y = 2,5(1,45)x ). Årsaken til avviket er at verdiene ble avlest diagrammet på skjermen. Diagrammet er lite og grafen tykk, hvilket øker usikkerheten ved avlesningen.
Resultatet er også en påminnelse om at man ikke bør ta slike avlesninger for absolutte sannheter.
e som grunntall
Det er svært vanlig å bruke tallet e som grunntall i eksponensialfunksjonenen.
Sammenhengen mellom et tilfeldig grunntall a og e er denne:
ax= (elna)x = elna· x
Der ln er den naturlige logaritmen.
Funksjonen fra eksempel 8 blir da: y = 2,5(1,45)x = 2,5eln1,45·x =2,5e0,372x
Fra plott til modell
Man har stor nytte av denne teorien dersom man har et sett med observasjoner og søker en matematisk sammenheng (modell).
Man måler surheten i en elv der en fabrikk har et utslipp. Man foretar målålinger rett ved utslippet, 5km nedenfor utslippet 10 km nedenfor utslippet og 50 km fra utslippet. Man foretar 3 målinger på hvert sted gjennom et år. På grunnlag av målingene ønsker man å se om det er mulig å lage en matematisk modell som sier noe om konsentrasjonen av H+ ioner x antall kilometer fra utslippsstedet. Målingene er:
0 km 10 km 50 km
Januar 1,7∙ 10-9 2,6∙ 10-9 1,3∙ 10-8 Mai 3,7∙ 10-9 5 ∙ 10-9 1,7∙ 10-8 Oktober 2,2∙ 10-8 1,7∙ 10-8 6 ∙ 10-9
Plottet i et log papir ser det slik ut:
Her ser man at punktene ligger på en rett linje (fordi de er oppkonstruerte). Dersom punktene ikke ligger på en rett linje, men antyder en lineær sammenheng kan man foreta en lineær kurvetilpassning.
Benytter man teorien i avsnittet om eksponentialfunksjonen får man følgende funksjoner for konsentrasjonen av H+ ioner finner man følgene sammenhenger:
Januar: y = (1,6 ∙ 10-9)e0,042x
Mai: y = (3,7 ∙ 10-9)e0,03x
Oktober: y = (2,2 ∙ 10-8)e-0,026x
Når man har sett av observasjonsdata kan det være et sterkt ønske å kunne lage en matematisk sammenheng av typen over. Man må imidlertid være klar over at ofte er det ingen sammenheng i det hele tatt. Det kan være fristene å "fikse" datamengden ved for eksempel å utelate data som "ikke passer". Ikke gjør det!