R1 2014 høst LØSNING: Forskjell mellom sideversjoner
| Linje 172: | Linje 172: | ||
===b)=== | ===b)=== | ||
Finner den eller de t verdier som gir skalarprodukt lik null: | |||
$ \vec {AC} = [t+1, t-1] \\ \vec{CB} = [1-t, 5-t]$ | |||
==Oppgave 4== | ==Oppgave 4== | ||
Sideversjonen fra 26. feb. 2016 kl. 18:44
- Løsning fra NDLA
- Diskusjon av denne oppgaven
- Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du oppdager feil i fasit. På forhånd, takk.
Feil i løsningsforslag:
Del 1 2a: Snek seg inn en trykkfeil for det skal stå +2x og ikke -2x i andregradspolynomet.
Del 2 4b forsvant i farten: Løs likningen T(x)=16/2 som gir x=1 og x=2.
DEL EN
Oppgave 1
a)
$f(x)=5x^3-2x^2+5 \\ f ` (x)=15x^2-4x$
b)
$g(x)= x^2 \cdot e^x \\ g`(x) = 2xe^x+ x^2e^x= xe^x(2+x)$
Oppgave 2
a)
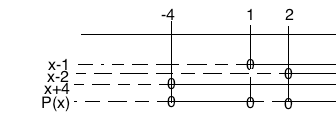
Her må vi prøve oss fram. Det lønner seg å begyne med det enkleste muligheter først. Man observerer at P(1) = 0 og vet da at P er delelig på (x-1):
$ \quad x^3+x^2-10x+8 : (x-1) = x^2+2x - 8 \\-(x^3-x^2) \\ \quad \quad \quad 2x^2-10x \\ \quad \quad -(2x^2-2x) \\ \quad \quad\quad \quad \quad -8x+8$
Ved å faktorisere andregradspolynomet får man røtter for x= -4 og x =2.
P faktorisert: ( x - 1) (x - 2)(x + 4).
b)
$ P(x)\leq 0 \\ x \in < \leftarrow, -4] \cup [1,2]$
Oppgave 3
a)
$L = 10 \cdot lg (\frac{I}{I_0}) \\ L = 10 (lg I - lg I_0) \\ L =10(lgI - lg 10^{-12}) \\ L = 10 lg I + 120 $
b)
$ L = 10 lg I + 120 \\ L = 10 \cdot lg 10^{-4}+120 \\ L = 80 $
Det er 80 db på arbeidsplassen.
c)
$L = 10 lg I + 120\\ 100 - 10lgI +120 \\ lg! =-2 \\ I = 10^{-2} $
Det svarer til $10^{-2} W/m^2$
Oppgave 4
a)
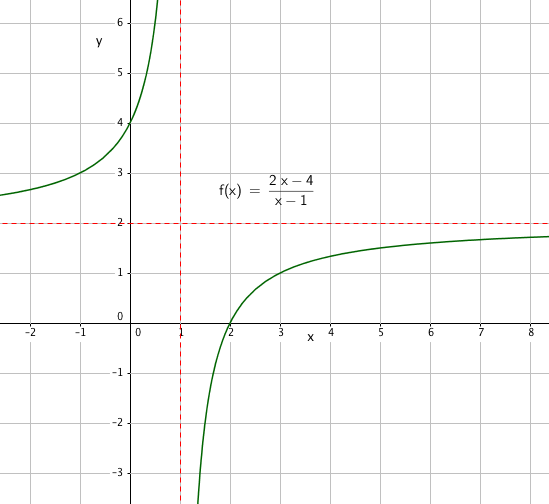
b)
$f´(x)= \frac{2(x-1)-(2x-4)}{(x-1)^2} = \frac {2}{(x-1)^2}$
c)
$f(2)=0 \\ f´(2)=2 \\ y=ax+b \\ 0 = 2 \cdot 2 + b \\ b= -4 \\ y=2x-4$
Oppgave 5
a)
Stigningstallet til linjen y= ax + b er a. Dvs. hvor mye man går opp eller ned på y aksen når man går en enhet til høyre på x- aksen, for å treffe linjen igjen. Det er nettopp det v vektor gjør.
b)
Dersom linjen står vinkelrett på hverandre er skalarproduktet mellom rettningsvektorene lik null.
$[1, a_1][1,a_2] = 0 \\ 1 + a_1 \cdot a_2= 0 \\ a_1 \cdot a_2=-1$
Oppgave 6
$ \frac 23 \cdot ( \frac 34)^{x^2-x} = \frac 38 \\ ( \frac 34)^{x^2-x} = ( \frac 34)^2 \\ x^2-x-2=0 \\ x= -1 \vee x= 2$
Oppgave 7
a)
$A_{ABCD} = a^2$
Lengden AC = $ \sqrt 2 a$
Areal stort kvadrat blir da:
$A_{AEFC} = ( \sqrt 2 a)^2 = 2 a^2$
Det store kvadratet har dobbelt så stort areale som det lille. Dett kan vi se lett ved geometriske betraktninger, siden ACD er lik BFC.
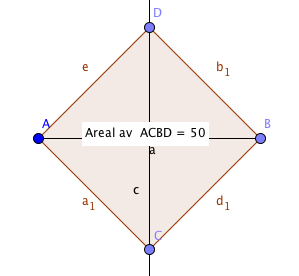
b)
Avsett et linjestykke AB = 10 cm. Kosntruer midtnormalen til AB, CD, slik at C ligger 5 cm under AB og D ligger 5 cm over linjestykke AB. Du har nå to diagonaler, AB og CD, begge på 10 cm. Disse utspenner et kvadrat ABCD på $50 cm^2$
Oppgave 8
$f(x) = x^3-x \\ f'(x)= 3x^2-1 \\ f'(x)= lim_{\Delta x \rightarrow 0} \frac{f(x+ \Delta x) - f(x)}{\Delta x} = \\ \lim_{\Delta x \rightarrow 0} \frac{(x+ \Delta x)^3-(x+ \Delta x) - (x^3 - x)}{\Delta x}= \\ \lim_{\Delta x \rightarrow 0} \frac{(x^2+ 2x \Delta x +( \Delta x)^2)(x + \Delta x)-x- \Delta x - x^3 + x)}{\Delta x} = \\ \lim_{\Delta x \rightarrow 0} \frac{x^3+2x^2 \Delta x +x( \Delta x)^2+x^2 \Delta x +2x( \Delta x)^2+( \Delta x)^3 - \Delta x - x^3}{\Delta x} = \\ \lim_{\Delta x \rightarrow 0} \frac{ \Delta x( 2x^2 + x \Delta x + x^2 +2x \Delta x + ( \Delta x)^2 - 1)}{\Delta x} = \\ 2x^2+x^2 - 1 = \\ 3x^2-1 $
DEL TO
Oppgave 1
a)
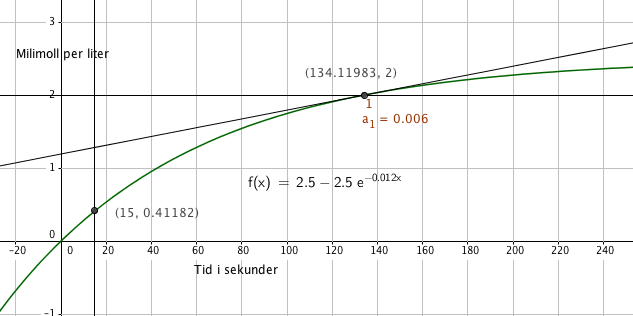
Fra Figuren ser man at etter 15 sek er den ca 0,41 millimol per liter.
Fra Figuren ser man at det tar ca 2 min og 14 sekunder, for å nå 2,0 millimol per liter.
b)
Graf tegnet i a.
Dersom t blir stor ser man at det siste leddet i funksjonsuttrykket går mot null og f går mot 2,5.
c)
Fra Figuren ser man at reaksjonshastigheten da er 0,006 millimol per liter, per sekund.
Oppgave 2
a)
Primtall er tall som kun er delleligge med seg selv og en: 2, 3, 5, 7, 11, 13, 17, 19, og 23.
b)
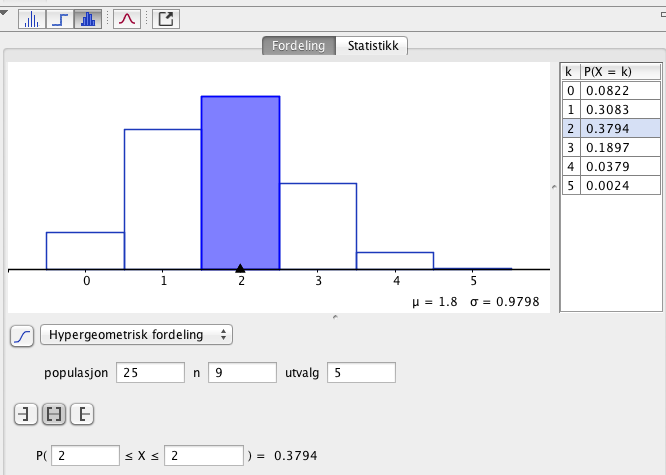
Vi har 25 tall, hvorav 9 primtall. Trkkning uten tilbakelegging. Dette er en hypergeometrisk situasjon:
Sannsynligheten for å trekke ut akkurat to primtall er 37,9%.
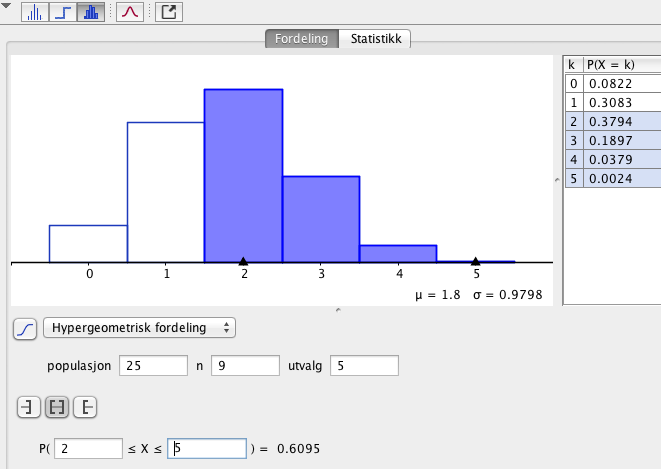
c)
Oppgave 3
a)
$ \vec{AB} =[2,4] \\ \vec{AC} = [t+1,t-1] \\ k \vec{AB} = \vec{AC} \\ 2k = t+1 \wedge 4k=t-1 \\ t=-3 $
Punktene ligger på linje dersom t = -3.
b)
Finner den eller de t verdier som gir skalarprodukt lik null:
$ \vec {AC} = [t+1, t-1] \\ \vec{CB} = [1-t, 5-t]$
Oppgave 4
a)
Areal trekant AEH + GFC: $x(4-2x) = 4x-2x^2$
Areal trekant HGD + EBF: $2x(4-x)= 8x-2x^2$
Areal av alle fire trekanter: $12x-4x^2$
Areal parallellogramm EFGH:
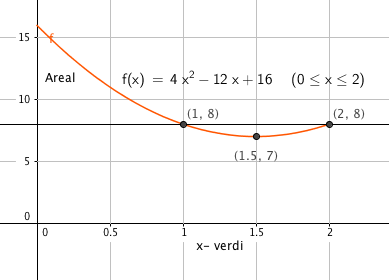
$T(x) = 16- ( 12x-4x^2) = 4x^2-12x+16$
b)
$T(x) = 8 \\ 4x^2-12x+8=0 \\x= 1\vee x=2$
Når x=1 eller når x=2 blir arealet av parallellogrammet halvparten av kvadratets areal.
c)
Fra Figuren ser man at arealet blir minst mulig når x = 1,5. Arealet er da 7.
d)
Skalarproduktet mellom HE vektor og HG vektor skal da være null.
$ \vec{HE} \cdot \vec{HG} = 0 \\ [x, -4+2x][4-x, 2x] =0 \\ 4x-x^2-8x+4x^2 =0 \\ x(3x-4)=0 \\ x=0 \vee x= \frac 43$
Dersom x=0 er EFGH et kvadrat, identisk med ABCD. x = 4/3 gir et innskrevet rektangel.
Oppgave 5
a)
B ( 5, 2)
C ( 1, 5)
y = ax + b
Stigningstall a: $\frac {\Delta y}{\Delta x} = \frac{2-5}{5-1} = - \frac 34$
$5 = - \frac 34 \cdot 1 + b \\ b= \frac {23}{4} \\ y = - \frac 34 x + \frac{23}{4}$
b)
Stigningstall:
$ \frac 12 a =-1 \\ a= -2$
Likning:
Punkt C (1, 5)
$y=ax+b \\ 5 = -2 \cdot 1 +b \\ b = 7 \\ y= -2x +7$
c)
Ser på linjene som går gjennom A og B først:
$\frac 43x + \frac 13 = - \frac 13x + \frac{11}{3} \\ 4x+1=-x+11 \\x=2$
Innsatt i $y= \frac 43x + \frac 13$ gir y = 3.
Setter x = 2 inn i y= -2x+7, og får y = -4+7 =3. Altså skjærer alle de tre høydene i punktet (2,3).
Oppgave 6
a)
Vinkel BAS er lik vinkel ABS. Vi kaller dem for x:
$u+2x =180 \\ 2x= 180-u \\ x = 90 - \frac u2$
b)
AS er radien i sirkelen og står følgelig vinkelrett på tangenten i A:
$v + 90 - \frac u2 = 90 \\ v = \frac u2$
Oppgave 7
a)
$f(x)= \frac uv \quad \quad u>0, \quad v>0 \\ (\ln f(x))´ = \frac 1u \cdot u´- \frac 1v \cdot v´= \frac{u´v-vú}{uv}$
b)
Vi husker resultatet fra oppgave a.
$( \frac uv)´ = (e^{\ln \frac uv})´ = e^{\ln \frac uv} \cdot \frac{u´v-vú}{uv} =\frac uv \cdot \frac{u´v-v`u}{uv} = \frac{uv´- v`u}{v^2}$