R1 2015 høst LØSNING: Forskjell mellom sideversjoner
| Linje 131: | Linje 131: | ||
===b)=== | ===b)=== | ||
Det er 36% som ikke har blå øyner. !8% av disse er gutter. Sannsynligheten er 0,5 for gutt. | |||
==Oppgave 8== | ==Oppgave 8== | ||
Sideversjonen fra 26. jan. 2016 kl. 19:09
Løsningsforslag laget av LektorH
Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du har kommentarer til løsningsforslaget. På forhånd, takk.
DEL EN
Oppgave 1
a)
$f(x)= 3x^2+5x-2 \\ f´(x)=6x+5$
b)
$g(x)=3(x^2-2)^4 \\g´(x)= 3 \cdot 4 \cdot 2x(x^2-3)^3 = 24x(x^2-3)^3$
c)
$h(x)= x ln(x^2+3)$
Setter $ u= x^2+3$ som gir u´= 2x, og får:
$h´(x)= ln(x^2+3)+ \frac{x \cdot 2x}{x^2+3} \\ h´(x)= ln(x^2+3) + \frac{2x^2}{x^2+3}$
Oppgave 2
$f(x)= xe^{-x} \\ f´x) = e^{-x} +x (-1) e^{-x} = e^{-x}(1-x)$
$e^{-x}$ er positiv for alle x. (1-x) er null for x=1, negativ for x > 1 og positiv for x < 1. x = 1 gir et maksimum for funksjonen.
Oppgave 3
a)
$f(x)=x^3-2x^2-kx+6, \quad D_F = \R$
k slik at $f(x):( x-1)$ går opp:
$1-2-k +6 =0 \\k = 5$
b)
$x^3-2x^2-5x+6 :(x-1)= x^2-x-6 \\-(x^3-x^2) \\ \quad \quad -x^2-5x \\ \quad \quad -(-x^2+x) \\ \quad \quad \quad \quad -6x+6 \\ \quad \quad\quad \quad -(-6x+6)$
Vi løser andregradspolynomet (abc - formel el.) og får totalt disse tre lineære faktorer: (x - 1)(x + 2)(x - 3).
c)
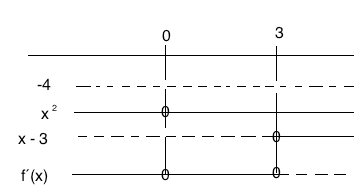
Tegner fortegnsskjema for hver av de tre lineære faktorene i b, og får fortegnslinjen for f(x):
Oppgave 4
$lg(a^2b^3)+ lg(\frac{1}{b^2}) - lg ( \frac{b}{a}) = \\ 2 lga + 3 lgb -2lgb - lgb + lga = \\ 3 lg a$
Oppgave 5
a)
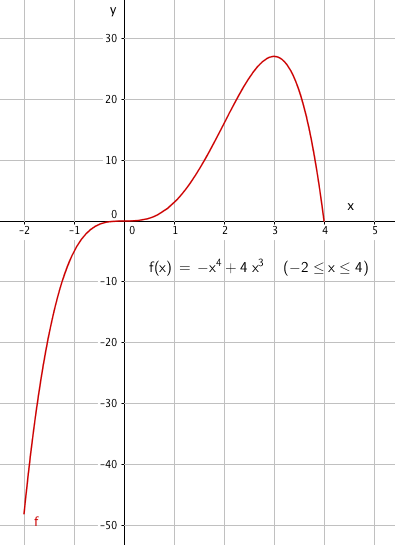
$f(x)=-x^4+4x^3 = x^3(-x+4) \quad x \in <-2, 4>$
Siden funksjonen ikke er definert for x = 4 har den bare ett nullpunkt, i Origo (0, 0).
b)
$f´(x) = -4x^3+12x^2 = -4x^2(x-3)$
Grafen har et terassepunkt for x = 0, dvs. i (0, 0) og et maksimum i (3, f(3)) som gir (3, 27).
c)
Vendepunkt:
$f´´(x)= -12x^2 + 24x \\ f´´(x)=0 \\ -12x(x-2) =0 \\ x=0 \vee x = 2$
x= 0 er sammenfallende med nullpunkt og terrassepunkt, vendepunktene er (0, 0) og (2, 16) ( f(2) = 16).
d)
Oppgave 6
Vinkel u spenner over samme bue som vinkel D. Begge ligger på sirkelperiferien og er derfor like. Vinkel u er 50 grader.
Vinkel C er 90 grader fordi den ligger på pereferien og spenner over diameteren. Da blir vikel v 40 grader.
Oppgave 7
a)
Siden det er 60% jenter og 70% av disse har blå øyner, betyr det at 42% av elevmassen er jenter med blå øyner. Tilsvarende tall for gutter er 22%.
| Blå | ikke blå | Total | |
| Jente | 42% | 18% | 60% |
| Gutt | 22% | 18% | 40% |
| Total | 64% | 36% | 100% |
Fra tabellen ser man at sannsynligheten for å trekke en elev med blå øyner er 64%.
b)
Det er 36% som ikke har blå øyner. !8% av disse er gutter. Sannsynligheten er 0,5 for gutt.