1P 2015 høst LØSNING

• Diskusjon av denne oppgaven på matteprat
• mer diskusjon av denne oppgaven på matteprat
• Løsningsforslag del 1 av jøgge

• oppgaven (bedre versjon kommer snart)
• oppgaven (bedre versjon)

Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du har kommentarer til løsningsforslaget. På forhånd, takk.

Oppgave 1

a)

$\frac {0,4}{1,0} = \frac{2,4}{x} \\ 0,4x = 2,4 \\ x= \frac{2,4}{0,4} \\ x= 6$

Man bør ikke spise mere enn 6 gram salt daglig.

b)

Dersom 100g inneholder 0,8g vil 300g inneholde tre ganger så mye:

$0,8g \cdot 3= 2,4g$ salt

En porsjon pizza inneholder 2,4 gram salt.

c)

$ 2,4 \cdot 0,4g = 0,96 g$ natrium.

$0,96 : 2,4 = \\ 9,6: 24= 0,4$

Dvs 40% av dagsbehovet.

Oppgave 2

a)

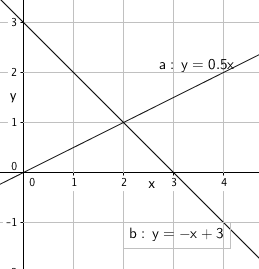
Ved avlesning: skjæringspunkt i (2, 1).

b)

$f(x)= g(x) \\ \frac 12x = -x+3 \\ x =-2x + 6 \\ 3x =6 \\ x=2$

f(2)= 1

Skjæringspunkt mellom f og g : (2,1)

Oppgave 3

Reallønn = nominell lønn $\cdot \frac{100}{ indeks} $

$360000= 450000 \cdot \frac {100}{x} \\ x = \frac{45000000}{360000} =125$

Konsumprisindeksen var på 125 det året.

Oppgave 4

Dersom omvendt proporsjonale størrelser: $y = \frac kx \\ xy=k$

20kr / is $\cdot$ 200 is = 4000 kr

25kr / is $\cdot$ 160 is = 4000 kr

40kr / is $\cdot$ 100 is = 4000 kr

Pris og antall er omvendt proporsjonale størrelser.

Oppgave 5

a)

Gutt: ( fars høyde + mors høyde) $\cdot$ 0,5 + 7 cm

Jente: ( fars høyde + mors høyde) $\cdot$ 0,5 - 7 cm

Ola: ( 180 cm + 160 cm) $\cdot$ 0,5 + 7 cm = 177 cm

Kari: ( 180 cm + 160 cm) $\cdot$ 0,5 - 7 cm = 163 cm

Kari blir 163 cm og Ola 177 cm, i følge formlene.

b)

( 186cm + mors høyde) $\cdot$ 0,5 + 7 cm = 189 cm.

$(186 +x) \cdot 0,5 +7 = 189 \\ (186+x) \cdot 0,5 = 182 \\ 186+x = 364 \\x= 178$

Mor er 178 centimeter høy, i følge formelen.

Oppgave 6

a)

Volum av sylinder: $V= \pi r^2 h$

Ved overslag runder man tallen til noe som blir letterer å regne med, samtidig som man ikke bør fjerne seg for langt fra de eksakte verdiene. Når man ganger sammen to eller flere tall kan det være lurt å runde noen opp og noen ned:

$V= \pi \cdot 0,6^2 \cdot 1,2 \\ \approx 3 \cdot 0,4 \cdot 1,2 \\ = 1,44$

Alle benevninger var i meter, det betyr at svaret er i kubikkmeter: $1,44m^3 = 1440 dm^3$, som er det samme som 1440 liter.

Volumet til en rundball er i størrelsesorden 1400 liter. (Om du fikk et annet svar kan det være like riktig siden dette kun er et overslag).

b)

Overflate av sylinder:

$O = 2 \pi r^2 + 2 \pi r h$

Setter Pi = 3 og

Oppgave 7

	Smittet	Ikke smittet	sum
Tester positivt	58	10	68
Tester ikke positivt	2	290	292
sum	60	300	360

b)

P( pos | smittet) = $\frac{58}{60} = \frac{29}{30}$

c)

P( ikke smittet | pos test) = $\frac{10}{68} = \frac{5}{34}$

Oppgave 8

$f(x)= -x$

Dette er en rett linje uten konstantledd, det betyr at grafen går gjennom origo. Den har stigningstall -1, (en til høyre, en ned) hvilket betyr a B er riktig graf.

$g(x) = -x^2+x+2$

Dette er en parabel eller andregradsfunksjon. Når det står minus forran andregradsleddet betyr det at den vender sin hule side ned. Den skjærer y-aksen i 2. Både graf A og F oppfyller disse kravene. Vi sjekker nullpunktet x = 2 for F: $- (2^2)+2+2 =0$. Graf F tillhører funksjonen g.

$h(x)= \frac 12x + 1$

En rett linje som skjærer y-aksen i en og stiger med en halv. Graf E passer til funksjon h.

Oppgave 1

a)

b)

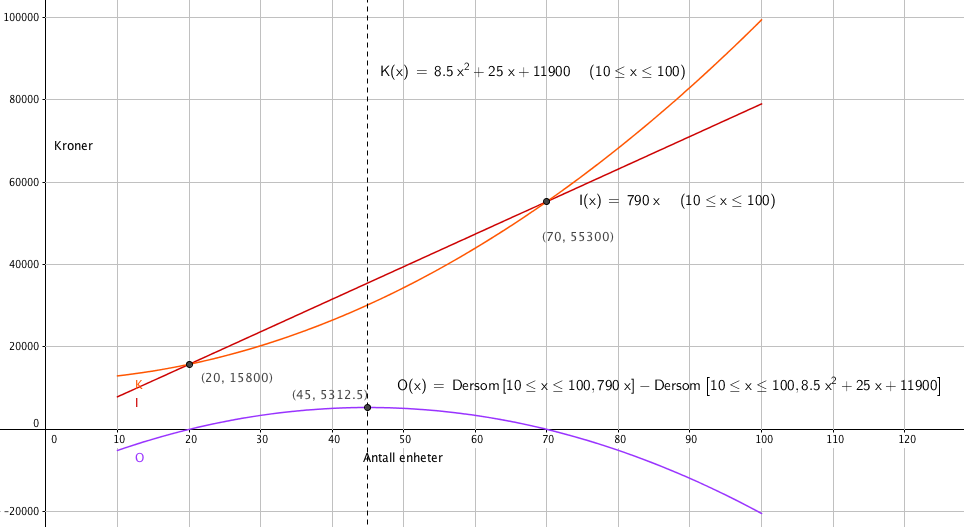
Kostnader og inntekter er like store for 20 og 70 enheter, fra figuren i a.

c)

For at overskuddet skal bli størst mulig må det produseres og selges 45 enheter. Overskuddet er da 5312,50 kroner.

Oppgave 2

a)

Dette er eksponentiell vekst, med vekstfaktor lik 0,85.

$V(2) = 8600 \cdot 0,85^2 = 6213,50$

Om to år er scooterens verdi ca 6200 kroner, i følge modellen.

b)

$x \cdot 0,85^3 = 8600 \\ x = 8600 \cdot 0,85^{-3} \\ x= 14003,66$

Når scooteren var ny kostet den 14 000 kroner.

Oppgave 4

a)

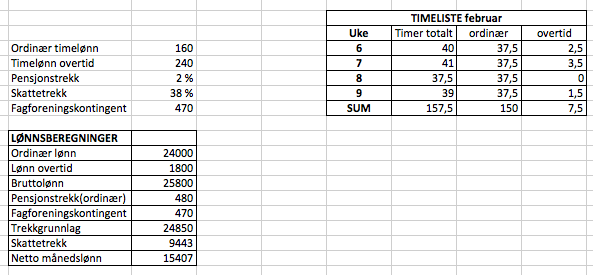
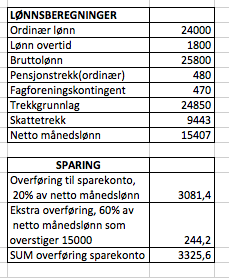
Nettolønna er 15 407 kroner i februar.

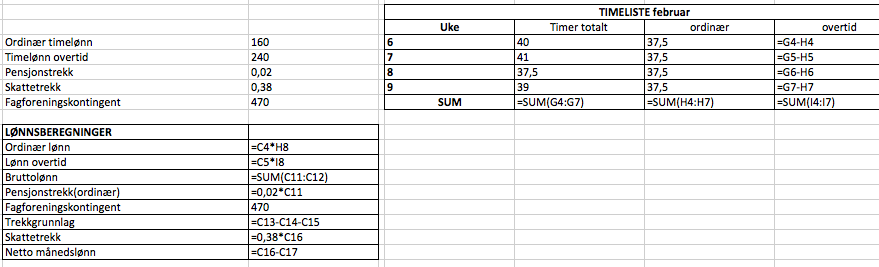
Formler:

b)

Hun overførte 3325,60 kroner til sparekontoen i februar.

Oppgave 5

a)

AF, bruker pytagoras: $AF = \sqrt{25-9} = 4$

Trekant ADF er formlik med trekant ABG.

c)

Vannet renner inn med konstant fart. Etter hvert som vannet stiger blir grunnflaten i kjeglestumpen større. For å fylle et gitt volum blir derfor høyden i kjeglestumpen mindre etter hvert som vannet stiger. Det betyr at vannet stiger saktere og saktere og at graf 3 illusterer dette.

Oppgave 6

a)

Jeg tolker det slik at det samme skoparet skal brukes tre dager på rad. Vi har parene A, B og C.

Sannsynlighet for å velge par A i tre dager: $\frac 13 \cdot \frac 13 \cdot \frac 13$

Men, det er tre par å trekke fra, AAA, BBB og CCC, derfor må man multiplisere med 3:

P(samme par tre dager på rad)= $3 \cdot \frac 13 \cdot \frac 13 \cdot \frac 13 = \frac 19 $

b)

Første dag kan han velge tre av tre, andre dag to av tre og siste dag en av tre:

P( forskjellige sko hver dag) = $1 \cdot \frac 23 \cdot \frac 13 = \frac 29$

Oppgave 7

a)

$40 km/h = \frac{40000m}{3600s} =11,1 m/s$

b)

Bremselengde sommerføre:

Fart 40 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(11,1 m/s)^2}{19,6 \cdot 0.8} = 7,9 m$

Fart 80 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(22,2 m/s)^2}{19,6 \cdot 0.8} = 31,5 m$

Bremselengde vinterføre:

Fart 40 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(11,1 m/s)^2}{19,6 \cdot 0.2} = 31,4 m$

Fart 80 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(22,2 m/s)^2}{19,6 \cdot 0.2} = 125,7 m$

c)

Når farten dobbles blir bremselengden tilnærmet firedobblet. Dette gjelder både sommer og vinter.

$\frac{31,5}{7,9} \approx \frac{125,7}{31,4} \approx 4$

Bremselengde og fart er ikke proporsjonale størrelser. Om de hadde vært det skulle den ene dobble seg når den andre dobbler seg.

d)

Fra utregningene i b ser man at farten på vinterstid bør halveres om man ønsker samme bremselengde.

$ v^2 = 19,5\cdot f \cdot s \\ \frac{v^2_{sommer}}{v^2_{vinter}} = \frac{19,6s \cdot 0,8}{19,6s \cdot 0,2} \\ \frac{v_{sommer}}{v_{vinter}} = \sqrt 4 = 2$