2P 2015 høst LØSNING: Forskjell mellom sideversjoner
| Linje 94: | Linje 94: | ||
1A: Gjennomsnitt: $\frac{5 \cdot 1 + 4 \cdot 2 + 2 \cdot 3 + 1 \cdot 4 + 3 \cdot 5 + 5 \cdot 6}{20} \\ \frac{68}{20} = 3,4$ | 1A: Gjennomsnitt: $\frac{5 \cdot 1 + 4 \cdot 2 + 2 \cdot 3 + 1 \cdot 4 + 3 \cdot 5 + 5 \cdot 6}{20} \\ \frac{68}{20} = 3,4$ | ||
1B: Gjennomsnitt: $\frac{1 \cdot 1 + 3 \cdot 2 + 5 \cdot 3 + 6 \cdot 4 + 4 \cdot 5 + 1 \cdot 6}{20} \\ \frac{68}{20} = 3,4$ | |||
===b)=== | ===b)=== | ||
Sideversjonen fra 11. des. 2015 kl. 14:28
DEL EN
Oppgave 1
70% er det samme som 280 kroner. 280: 70 = 4. Dvs 1% er 4 kroner. Da er 100% lik 400 kroner. (Finnes flere andre, mer elegante måter å gjøre det på også).
Oppgave 2
$3,4 \cdot 10^9 \cdot 4 \cdot 10^{-3} \\ 3,4 \cdot 4 \cdot 10^{9-3}\\ 13,6 \cdot 10^{6} \\ 1,36 \cdot 10^7$
Oppgave 3
$\frac{4^3\cdot 2^{-6}}{4^0 \cdot 2^{-2}}= \\ \frac{(2^2)^3 \cdot 2^{-6}}{1 \cdot 2^{-2}}= \\ 2^{6-6-(-2)}= \\ 2^2= 4$
Oppgave 4
Beløpet hun vant: x
Vekstfaktor til 3,2%: 1,032
Tid: 10 år
Uttrykk : $x \cdot 1,032^{10} = 500138 \\ x= 500138 \cdot 1,032^{-10}$
Oppgave 4
Omkrets av jorden: 40 000km = 40 000 000 meter.
Antall personer: $\frac{40000000}{1,6}= \\ \frac{4\cdot 10^{7}}{1,6} = \\ 2,5 \cdot 10^7$
Altså ca. 25 millioner mennesker (mange av dem må være svømmedyktige).
Oppgave 5
Oppgave 6
Oppgave 7
a)
Vi har to punkter og skal lage en lineær modell, (1,60) og (5,90). På 4 uker øker treningsmengden med 30 minutter.
På en uke øker den med $30: 4= 7,5$ som er det vi kaller stigningstallet. Likningen for en rett linje er gitt som
y= ax + b.
I vårt tillfälle blir det
y= 7,5x + b
Vi bruker første punktet (1, 60) og setter inn for x og y og får
$60 = 7,5 \cdot 1 + b \\ b= 60 - 7,5 \\ b= 52,5$
Modellen blir da
y = 7,5x + 52,5
b)
I uke 40 betyr det at x = 40 i uttrykket:
$y = 7,5 \cdot 40 + 52,5 \\ y = 300 + 52,5 \\ y = 352,5 \quad minutter$
Hun må trene 5 timer og 52 minutter og 30 sekunder, eller ca. seks timer i uken.
Oppgave 8
Vi leser av figuren i oppgaven og ser at startverdien er 10 000 bakterier. Etter en time er det 9000 bakterier. Det betyr at antall bakterier minker med 10% per time. Det gir en vekstfaktor på 0,90.
Uttrykket blir da: $B(x)= 10000 \cdot 0,90^x$
Der x er tidsenheter, i dette tilfelle timer.
Oppgave 9
a)
Det er 20 elever i hver klasse!!! (Altså et sted uten stykkprisfinansiering).
1A: Gjennomsnitt: $\frac{5 \cdot 1 + 4 \cdot 2 + 2 \cdot 3 + 1 \cdot 4 + 3 \cdot 5 + 5 \cdot 6}{20} \\ \frac{68}{20} = 3,4$
1B: Gjennomsnitt: $\frac{1 \cdot 1 + 3 \cdot 2 + 5 \cdot 3 + 6 \cdot 4 + 4 \cdot 5 + 1 \cdot 6}{20} \\ \frac{68}{20} = 3,4$
b)
c)
d)
Oppgave 10
a)
Det er fire markante temperaturfall på vannet, derfor er det fire pesoner som dusjer, dersom de dusjer en og en.
b)
Den lengste dusjperioden er på ca. 12,5 minutter. I den perioden faller temperaturen 4 grader. Den siste som dusjer, bruker 10 minutter, men da er temperaturfallet over 6 grader ( ikke en del av spørsmålet, men en interesant observasjon).
c)
DEL TO
Oppgave 1
Oppgave 2
a)
b)
c)
d)
Oppgave 3
Oppgave 4
Oppgave 5
Oppgave 6
a)
b)
c)
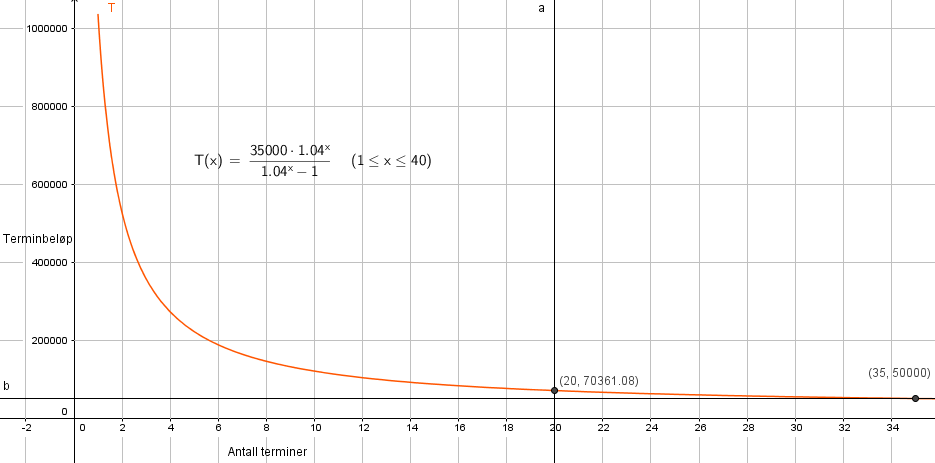
Fra figuren i b ser man at 20 terminer gir et terminbeløp i overkant av 70 000 kroner.
d)
Fra figuren i b ser man at et terminbeløp på 50 000 kroner, gir 35 terminer.
Oppgave 7
a)
Man ser at i det første kvadratet er arealet av det sorte kvadratet lik 1. I den andre kvadratet er arealet av et sort kvadrat $2^2$, og antall kvadrater er også $2^2$. Det totale arealet blir da $A(2)= 2^2 \cdot 2^2 = 2^4$. I den tredje figuren er arealet av ett sort kvadrat lik $3^2$ og antallet er $3^2$. Det totalearealet av sorte kvadrater i figur tre er da $A(3)= 3^2 \cdot 3^2 = 3^4$. Figur n vil da ha et totalt sort areal på $A(n)= n^4$.
Figur fire: $A(4)= 4^4 = 256$
b)
Se oppgave a.
c)
Figuene er
1, 2, 3.
Kvadratet av disse er:
1, 4, 9.
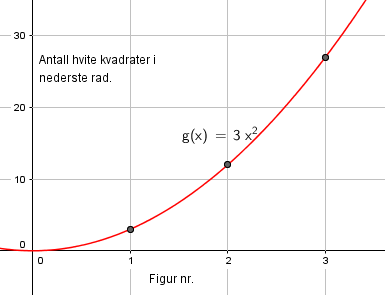
Antall hvite kvadrater på nederste rad er:
3, 12, 27.
Man observerer at kvadratet av figurnummeret må multipliseres med 3 for å få antall hvite kvadrater på nederste rad: $S(n)= 3n^2$
Løst ved regresjon på Geogebra:
d)
Det totale antall hvite kvadrater er:
Antall kvadrater minus antall svarte kvadrater, som er $(S(n))^2 - n^4 = \\ (3n^2)^2 - n^4 =\\9n^4-n^4=\\ 8n^4$