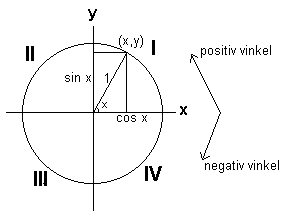Trigonometriske identiteter: Forskjell mellom sideversjoner
| Linje 169: | Linje 169: | ||
Skalarprodukt: | Skalarprodukt: | ||
$ [\cos u, \sin u] \cdot [\cos v, \sin v] = 1 \cdot 1 \cdot \cos(v-u) \\ \cos(v-u) = \cos u \cos v + \sin u \sin v$ | $ [\cos u, \sin u] \cdot [\cos v, \sin v] = 1 \cdot 1 \cdot \cos(v-u) \\ \cos(v-u) = \cos u \cos v + \sin u \sin v$ | ||
Sideversjonen fra 16. jul. 2015 kl. 16:03
Nedenfor følger en rekke trigonometriske identiteter. Noen er pensum i norsk skole (R2), andre ikke. Vi mener det er riktig å vise alle, da noen av dere kan komme til å studere i land der disse er pensum.
Spisse vinkler
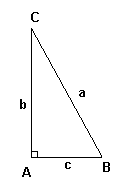
De trigonometriske funksjonene er sinus, cosinus, tangens, cotangens, secans og cosecans. De tre første er de vanligste. Vanligvis forkortes disse sin, cos, tan, cot, sec og cosec. For spisse vinkler defineres de trigonometriske funksjonene som forholdet mellom sidene i en rettvinklet trekant. Vi har:
• <math>sin B = \frac ba </math>
• <math>cos B = \frac ca </math>
• <math>tan B = \frac bc = \frac{sin B}{ cos B}</math>
• <math>cot B = \frac cb = \frac{ cos B}{sin B} = \frac {1}{tan B}</math>
• <math>sec B = \frac ac = \frac{1}{cos B}</math>
• <math>cosec B = \frac ab = \frac{1}{sin B} </math>
Enhetssirkelen
De trigonometriske funksjonene begrenser seg ikke til spisse vinkler. Vi tegner en sirkel med radius 1 der positive vinkler kan tenkes framkommet ved en dreining mot klokken og negative vinkler fremkommer ved dreining med klokken. dette kalles orienterte vinkler. I enhetssirkelen ser vi på orienterte vinkler med absolutte vinkelmål (radianer). Enhetsirkelen legges med sentrum i origo i et ortonormert koordinatsystem, slik at et av vinkelbeina er sammenfallende med den positive x aksen. Det andre vinkelbeinet skjærer sirkelen i punktet (x,y). De trigonometriske funksjonene defineres som følger:
<math> sin (a) = y \quad \quad cos (a) = x \quad \quad tan (a) = \frac yx \\ \\ cot (a) = \frac xy \quad \quad sec (a) = \frac 1x \quad \quad cosec (a) = \frac 1y </math>
Sin, cos, sec og csc har alle perioden $2\pi$. Tan og cot har perioden $\pi$.
Enhetssirkelen og dens fire kvadranter
Ved observasjon ser vi at fortegnet til en trigonometrisk funksjon varierer avhengig av hvilken kvadrant man befinner seg i. Nedenfor følger en oversikt.
| Kvadrant | I | II | III | IV |
| cos | pos | neg | neg | pos |
| sin | pos | pos | neg | neg |
| tan | pos | neg | pos | neg |
| cot | pos | neg | pos | neg |
| sec | pos | neg | neg | pos |
| cosec | pos | pos | neg | neg |
Geometrisk tolkning
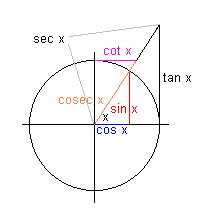
Geometrisk tolkning av de trigonometriske funksjonene. Figuren nedenfor viser de forskjellige trigonometriske funksjonene inntegnet i enhetssirkelen.
Definisjoner:
Det finnes mange trigonometriske identiteter. Her er noen av dem.
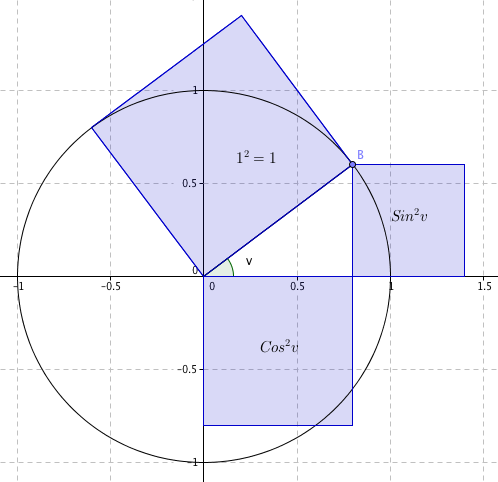
$sin^2v + cos^2v = 1$
Relasjonen fremkommer ved å anvende Pytagoras direkte i enhetssirkelen.
$ \quad \quad tan^2v + 1 = sec^2v\quad \quad cot^2v+1 = csc^2v$
| Uttrykt ved | <math> \sin v\!</math> | <math> \cos v\!</math> | <math> \tan v!</math> | <math> \csc v\!</math> | <math> \sec v\!</math> | <math> \cot v\!</math> |
|---|---|---|---|---|---|---|
| <math> \sin v =\!</math> | <math> \sin v \! </math> | <math>\pm\sqrt{1 - \cos^2 v}\! </math> | <math>\pm\frac{\tan v}{\sqrt{1 + \tan^2 v}}\! </math> | <math> \frac{1}{\csc v}\! </math> | <math>\pm\frac{\sqrt{\sec^2 v - 1}}{\sec v}\! </math> | <math>\pm\frac{1}{\sqrt{1 + \cot^2 v}}\! </math> |
| <math> \cos v =\!</math> | <math>\pm\sqrt{1 - \sin^2 v}\! </math> | <math> \cos v\! </math> | <math>\pm\frac{1}{\sqrt{1 + \tan^2 v}}\! </math> | <math>\pm\frac{\sqrt{\csc^2 v - 1}}{\csc v}\! </math> | <math> \frac{1}{\sec v}\! </math> | <math>\pm\frac{\cot v}{\sqrt{1 + \cot^2 v}}\! </math> |
| <math> \tan v =\!</math> | <math>\pm\frac{\sin v}{\sqrt{1 - \sin^2 v}}\! </math> | <math>\pm\frac{\sqrt{1 - \cos^2 v}}{\cos v}\! </math> | <math> \tan v\! </math> | <math>\pm\frac{1}{\sqrt{\csc^2 v - 1}}\! </math> | <math>\pm\sqrt{\sec^2 v - 1}\! </math> | <math> \frac{1}{\cot v}\! </math> |
| <math> \csc v =\!</math> | <math> \frac{1}{\sin v}\! </math> | <math>\pm\frac{1}{\sqrt{1 - \cos^2 v}}\! </math> | <math>\pm\frac{\sqrt{1 + \tan^2 v}}{\tan v}\! </math> | <math> \csc v\! </math> | <math>\pm\frac{\sec v}{\sqrt{\sec^2 v - 1}}\! </math> | <math>\pm\sqrt{1 + \cot^2 v}\! </math> |
| <math> \sec v =\!</math> | <math>\pm\frac{1}{\sqrt{1 - \sin^2 v}}\! </math> |
<math> \frac{1}{\cos v}\! </math> | <math>\pm\sqrt{1 + \tan^2 v}\! </math> | <math>\pm\frac{\csc v}{\sqrt{\csc^2 v - 1}}\! </math> | <math> \sec v\! </math> | <math>\pm\frac{\sqrt{1 + \cot^2 v}}{\cot v}\! </math> |
| <math> \cot v =\!</math> | <math>\pm\frac{\sqrt{1 - \sin^2 v}}{\sin v}\! </math> | <math>\pm\frac{\cos v}{\sqrt{1 - \cos^2 v}}\! </math> | <math> \frac{1}{\tan v}\! </math> | <math>\pm\sqrt{\csc^2 v - 1}\! </math> | <math>\pm\frac{1}{\sqrt{\sec^2 v - 1}}\! </math> | <math> \cot v\! </math> |
Sum og differanser av vinkler
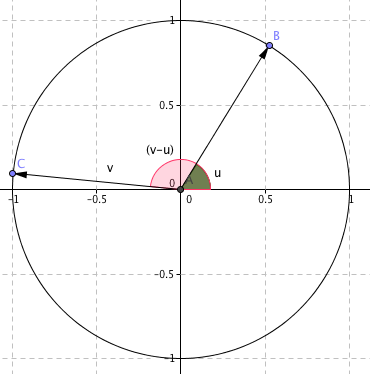
Vinkelen (v-u) er vinkelen mellom vektorene $\vec{OB}$ og $\vec{OC}$ Begge disse har lengde en.
$\vec{OB}= [\cos u, \sin u] \\ \vec{OC} = [\cos v, \sin v]$
Skalarprodukt:
$ [\cos u, \sin u] \cdot [\cos v, \sin v] = 1 \cdot 1 \cdot \cos(v-u) \\ \cos(v-u) = \cos u \cos v + \sin u \sin v$
$cos(u-v) = cos(u)\cdot cos(v)+sin(u) \cdot sin(v) \quad \quad cos(u + v) = cos(u)\cdot cos(v)-sin(u)\cdot sin(v) \\ sin(u - v) = sin(u)\cdot cos(v)-cos(u)\cdot sin(v) \quad \quad sin(u + v) = sin(u)\cdot cos(v)+cos(u)\cdot sin(v)$
Dobble vinkler
<math>sin(2u) = 2sin(u) \cdot cos(u) </math>
<math>cos(2u) = cos^2 (u) - sin^2 (u) </math>
<math>1 + cos(2u) = 2 cos^2 (u)</math>
<math>1 - cos(2u) = 2 sin^2 (u)</math>
Dersom u + v = 180° har vi at Sin v = sin u og cos v = -cos u