Trigonometriske identiteter: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| Linje 6: | Linje 6: | ||
$sin^2v + cos^2v = 1 | $sin^2v + cos^2v = 1$ | ||
[[File:pyt_1.png]] | |||
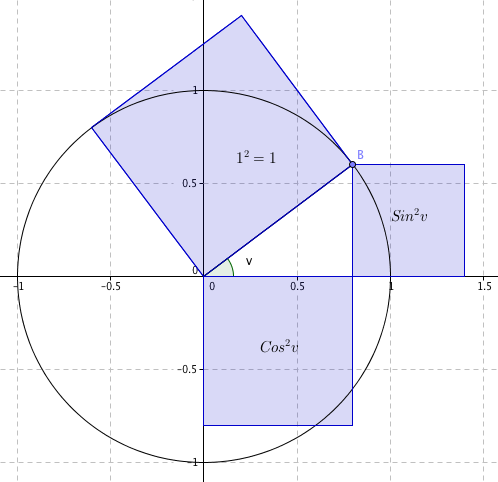
Relasjonen fremkommer ved å anvende Pytagoras direkte i enhetssirkelen. | Relasjonen fremkommer ved å anvende Pytagoras direkte i enhetssirkelen. | ||
$ \quad \quad tan^2v + 1 = sec^2v\quad \quad cot^2v+1 = csc^2v$ | |||
Sideversjonen fra 15. jul. 2015 kl. 11:40
Nedenfor følger en rekke trigonometriske identiteter. Noen er pensum i norsk skole (R2), andre ikke. Vi mener det er riktig å vise alle, da noen av dere kan komme til å studere i land der disse er pensum. Ha oss tilgitt, ikke alt er like lett å vise grafisk, men vi prøver så godt vi kan.
Definisjoner:
Det finnes mange trigonometriske identiteter. Her er noen av dem.
$sin^2v + cos^2v = 1$
Relasjonen fremkommer ved å anvende Pytagoras direkte i enhetssirkelen.
$ \quad \quad tan^2v + 1 = sec^2v\quad \quad cot^2v+1 = csc^2v$
$cos(u-v) = cos(u)\cdot cos(v)+sin(u) \cdot sin(v) \quad \quad cos(u + v) = cos(u)\cdot cos(v)-sin(u)\cdot sin(v) \\ sin(u - v) = sin(u)\cdot cos(v)-cos(u)\cdot sin(v) \quad \quad sin(u + v) = sin(u)\cdot cos(v)+cos(u)\cdot sin(v)$
<math>sin(2u) = 2sin(u) \cdot cos(u) </math>
<math>cos(2u) = cos^2 (u) - sin^2 (u) </math>
<math>1 + cos(2u) = 2 cos^2 (u)</math>
<math>1 - cos(2u) = 2 sin^2 (u)</math>
Dersom u + v = 180° har vi at Sin v = sin u og cos v = -cos u