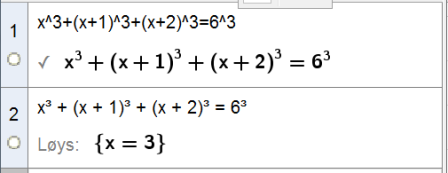S2 eksempeloppgave 2015 vår LØSNING

Oppgave 1

a)

$f(x)=3x^3-2x+5 \\ f'(x)=3\cdot 3x^{2}-2=9x^{2}-2$

b)

$g(x)=xe^{2x} \\ g'(x)=1⋅e^{2x}+x⋅2e^{2x}=(1+2x) e^{2x}$

Oppgave 2

Bestem $h'(2)$ når $h(x)=\frac{e^x}{x-1}$

$h'(x)=\frac{e^x⋅(x-1)-e^x⋅1}{(x-1)^2}=\frac{xe^x-e^x-e^x}{(x-1)^2} =\frac{xe^x-2e^x}{(x-1)^2} =\frac{(x-2) e^x}{(x-1)^2} \\ h'(2)=\frac{(2-2) e^2}{(2-1)^2} =\frac{0⋅e^2}{1}=0 $

Oppgave 3

$P(x)=2x^3-6x^2-8x+24$

a)

$P(3)=2⋅3^3-6⋅3^2-8⋅3+24\\ =2⋅27-6⋅9-24+24\\ =54-54-24+24=0 $

b)

Vi har vist at $P(x)=0$ for $x=3$. Då seier nullpunktsetninga at polynomdivisjonen $P(x):(x-3)$ går opp.

$(2x^3-6x^2-8x+24):(x-3)=2x^2-8$

Faktoriserer $2x^2-8$:

$2x^2-8=2(x^2-4)=2(x-2)(x+2)$

$P(x)=(2x^2-8)(x-3)=2(x-2)(x+2)(x-3)$

c)

$\frac{2x^3-6x^2-8x+24}{2x^2-8}=\frac{2(x-2)(x+2)(x-3)}{2(x-2)(x+2)} =(x-3)$

Oppgave 4

a)

$n$	$a_n$	$S_n$	$S_n$
1	1	1	$1^3$
2	7	8	$2^3$
3	19	27	$3^3$
4	37	64	$4^3$
5	61	125	$5^3$
6	91	216	$6^3$

Formel for $S_{n}$:

$S_{n}=n^3$

b)

$S_n$ er summen av dei $n$ første ledda

$S_n=a_1+a_2+...+a_{n-1}+a_n$

$S_{n-1}$ er summen av dei $(n-1)$ første ledda:

$S_{n-1}=a_1+a_2+...+a_{n-1}$

Vi får at: $S_n=S_{n-1}+a_n \\ a_n=S_n-S_{n-1}$

$a_n=S_n-S_{n-1} \\ a_n=n^3-(n-1)^3 \\ =n^3-(n-1) (n-1)^2 \\ =n^3-(n-1)(n^2-2n+1) \\ =n^3-n^3+2n^2-n+n^2-2n+1\\ =3n^2-3n+1$

Oppgave 5

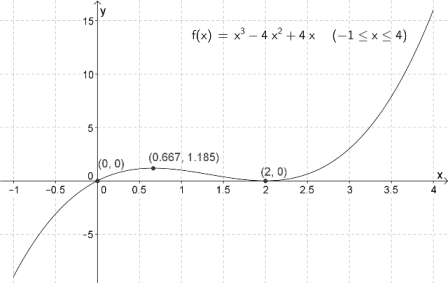
$f(x)=x^3-4x^2+4x , \space x∈〈-1,4〉$

a)

Nullpunkt:

$f(x)=0 \\ x^3-4x^2+4x=0 \\ x(x^2-4x+4)=0 \\ x=0 \vee x^2-4x+4=0 \\ x=0 \vee (x-2)^2=0 \\ x=0 \vee x=2 $

Nullpunktene er $x=0$ og $x=2$.

Topp-/bunnpunkt:

$f'(x)=3x^2-8x+4$

$f'(x)=0 \\ 3x^2-8x+4=0 \\ x=\frac{-(-8)±\sqrt{(-8)^2-4⋅3⋅4}}{2⋅3}=\frac{8±\sqrt{64-48}}{6}=\frac{8±\sqrt{16}}{6}=\frac{8±4}{6} \\ x=2 \vee x=\frac{2}{3} $

$3x^2-8x+4=3(x-2)(x-\frac{2}{3}) $

(Sett inn fortegnslinje)

$f(2)=0 \\ f(\frac{2}{3})=\frac{32}{27} $

Toppunktet er $(\frac{2}{3},\frac{32}{27})$ . Bunnpunktet er $(2,0)$.

b)

Oppgave 6

$f(0)=300, \space f'(10)=0 $ og $f' '(10)=-10 $

Ved starten av utbruddet, når $t=0$ er spruter det ut 300 tonn lava per time.

Etter 10 timer er veksten lik 0. Fordi den andrederiverte er negativ for $t=10$, vet vi at dette må være et toppunkt. Etter 10 timer er mengden lava per time størst.

Mengden lava per time øker fram til det har gått 10 timer, for deretter å avta.

Oppgave 7

Overskudd er inntekter minus kostnader.

$O(x)=I(x)-K(x)$

Overskuddet er størst når $O'(x)=0$ (Toppunktet på grafen til $O(x)$)

Vi deriverer og får: $ O'(x)=I' (x)-K' (x) $

$O' (x)=0 \\ \Updownarrow \\ I' (x)-K' (x)=0 \\ I' (x)=K'(x) $

Når grensekostnaden er lik grenseinntekta er overskuddet størst.

Oppgave 8

a)

$x=95$ gir

$z=\frac{x-μ}{σ}=\frac{95-100}{15}=\frac{-5}{15}=-\frac{1}{3} \approx -0,33$

$P(X≤95)=P(Z≤-0,33)=0,3707$

Sannsynligheten for at en tilfeldig valgt person vil skåre mindre enn 95 poeng, er ca. 37 %.

b)

Vi skal finne den $z$-verdien, som gjør at sannsynligheten $P(Z≥z)=0,02$.

Det er det samme som at $P(Z≤z)=0,98$. I tabellen for standard normalfordeling finner vi at det er $z=2,05$.

Vi kan nå regne om og finne $x$.

$ z=\frac{x-μ}{σ} \Rightarrow \\ 2,05=\frac{x-100}{15} \\ 30,75=x-100 \\ x=130,75 $

Du må minst skåre 131 poeng for å kunne bli medlem av Mensa.

Oppgave 9

Tabellen gir følgende likningssystem:

$ 3x+2y+4z=120 \\ 2x+3y+2z=75 \\ 2x+5y+3z=105 $

Løsning: $ x=10,y=5$ og $z=20 $

Oppgave 10

a)

Rekken er geometrisk fordi forholdet mellom et ledd og leddet foran er konstant med $k=\frac{2}{9}$.

Rekken konvergerer, fordi $-1<k<1$.

Summen blir:

$S=\frac{a_1}{1-k}=\frac{7}{1-\frac{2}{9}}=\frac{7}{\frac{7}{9}}=9$

b)

Summen av ballen sine høyder kan vi skrive slik:

$10+\frac{2}{3} \cdot 10 + \frac{2}{3} \cdot \frac{2}{3} \cdot 10 + ... $

Vi kan se på dette som en geometrisk rekke med

$a_1=10$ og $k=\frac{2}{3}$.

Rekken er konvergent, fordi $-1<k<1$.

Da blir $s=\frac{a_1}{1-k}=\frac{10}{1-\frac{2}{3}}=\frac{10}{\frac{1}{3}}=30$

Ballen skal opp og ned, bortsett fra for den første høyden. (Den blir sleppt fra 10 m.)

Den totale lengden blir derfor: $2\cdot 30$ m $ - 10 $ m $= 50 $ m.

Oppgave 11

$f(x)=(x-1) \cdot e^x, \quad x\in \langle 3, 2 \rangle $

a)

Skjæring med y-aksen:

$f(0)=(0-1)⋅e^0=-1⋅1=-1$

Skjæring med x-aksen:

$f(x)=0 \\ (x-1) \cdot e^x=0 \\ x-1=0 \\ x=1 $

Koordinatene til skjæringspunktene er $(0, -1)$ og $(1, 0)$.

b)

$f'(x)=1 \cdot e^x+(x-1) e^x =(1+x-1) \cdot e^x =x \cdot e^x$

$f'(x)=0 \\ x \cdot e^x=0 \\ x=0 $

(Lager fortegnslinje.)

Grafen til $f$ har et bunnpunkt i $(0, -1)$.

c)

Grafen synker raskest når $f' ' (x)=0$.

$f' '(x)=1⋅e^x+x⋅e^x=(1+x) e^x $

$f' '(x)=0 \\ (1+x) e^x=0 \\ 1+x=0 \\ x=-1 $

(Lager fortegnslinje.)

$f(-1)=(-1-1) e^{-1}=-2e^{-1}=-\frac{2}{e}$

Grafen til $f$ synker raskest i punktet $(-1,-\frac{2}{e})$.

Oppgave 1

a)

Svar: $n=12$ og $m=9$.

b)

Tre påfølgende tall, kan vi skrive som $x$, $x+1$ og $x+2$.

Vi får da denne likningen for summen av tre påfølgende kubikktall:

$x^3+(x+1)^3+(x+2)^3=6^3$

De tre kubikktallene er $3^3$, $4^3$ og $5^3$.

Oppgave 2

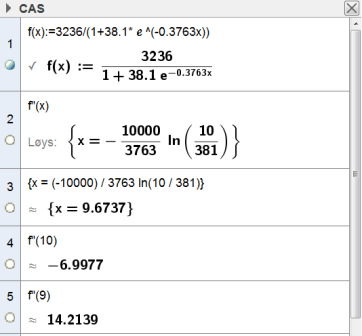
For å finne når fondet har størst vekst, må vis løse likningen $f' '(x)=0$ og vise at $f' '(x)$ skifter fortegn i dette punktet. Deretter kan vi sette løsningen inn i $f'(x)$ og $f(x)$. Jeg bruker CAS i GeoGebra.

Fondet har størst vekst i det 9. året etter 1996, det vil si i 2005.

Da er veksten ca. 304,43 milliarder kroner i året.

Fondet er på ca. 1616,87 milliarder kroner på det tidspunktet.

Oppgave 3

a)

$E(x)$ er kostnader per enhet. Det kan vi skrive slik:

$E(x)=\frac{K(x)}{x}$

Slik kan vi finne et uttrykk for totalkostnaden:

$K(x)=E(x) \cdot x = (0,15x+7+\frac{2000}{x}) \cdot x \\ K(x)=0,15x^2+7x+2000$

Uttrykket for inntekten, finner vi ved å gange inntekt per enhet med antall enheter.

$I(x)=55x$

b)

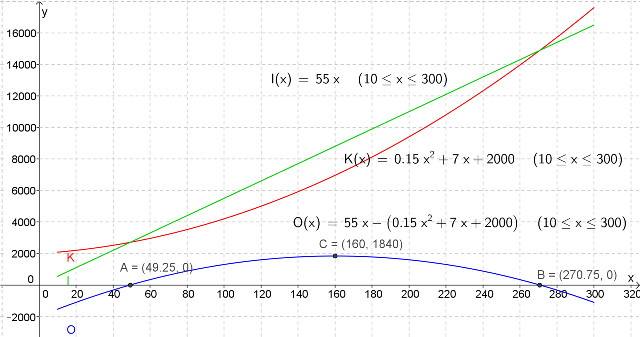
Jeg har løst denne oppgaven grafisk i GeoGebra.

Funksjonen for overskuddet finner jeg ved å skrive inn: $O(x)=I(x)-K(x) $.

Jeg finner skjæringspunktene $(49,25, \, 0)$ og $(270,75,\, 0)$ mellom grafen til $O(x)$ og $x$-aksen ved å bruke kommandoen «Nullpunkt». (Punkt A og B på grafen.)

Jeg finner toppunktet $(160, 1840)$ til grafen til $O(x)$ ved å bruke kommandoen «Ekstremalpunkt». (Punkt C på grafen.)

Produksjonsmengder mellom 50 og 270 enheter gir overskudd.

Det største overskuddet har bedriften ved produksjon av 160 enheter.