S1 2013 vår LØSNING

Oppgave 1

a)

$2lgx + 3 = 5 \\ 2lgx =2 \\ lg x=1 \\ 10^{lgx} 10^1 \\x=10$

b)

$2x^2+2x=12\\ 2x^2+2x-12=0 \\ x= \frac{-2\pm \sqrt{4+4 \cdot 2 \cdot 12}}{4} \\ x= \frac{-2 \pm 10}{4} \\ x= -3 \vee x= 2$

Oppgave 3

a)

$ \frac{2^{-3} \cdot a^0 \cdot (a \cdot b)^2}{2^{-4} \cdot a^{-1} \cdot b^2}= \frac{2^4a^3b^2}{2^3b^2} = 2a^3$

b)

$lg(ab) ^2- lg ( \frac{a^3}{b^2}) + lg(ab^2)= \\ 2(lga +lgb) - ( lg a^3 - lg b^2 ) + lga + lg b^2 = \\ 2lga+ 2lgb -3lga + 2lgb +lga + 2lgb = \\ 6 lgb$

Oppgave 4

a)

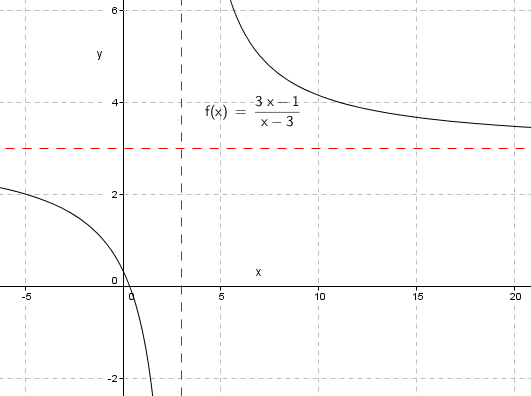
Her er grafen tegnet i Geogebra. Dette er del en, så det kan ikke du gjøre. Gjør slik:

Finn vertikal asymptote, den x verdi som gjør nevner lik null. x - 3 = 0 gir løsning for x = 3. Tegn asymptoten inn i koordinatsystemet.

Finn horrisontal asymptote. Del alle ledd i teller og nevner med x. Da får du: $\frac{3- \frac 1x}{1 - \frac 3x}$ Når absoluttverdien av x blir stor, går verdien av uttrykket mot 3. Tegn den horrisontale asymptoten inn i koordinatsystemet.

Lag en verditabell der du velger seks x verdier, tre mindre enn x = 3, og tre større. For eksempel x lik -5, 0, 2 og 4, 6 og 8. Regn ut funksjonsverdien for disse og plott punktene i koordinatsystemet. Trekk glatte kurver. Skissen av funksjonen bør ligne på den over.

b)

Gjennomsnittlig veksthastighet fra x = 4 til x = 7: $\frac{f(7) - f(4)}{3} = \frac{5-11}{3} =-2$

Den gjennommsnittlige vekstfarten fra x= 4 til x =7 er - 2.

Oppgave 5

a)

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

b)

Husk at det første tallet står på nullte rad.

$\binom 20 = 1$ (første tall på rad nr. tre, som jo egentlig er rad nr. to, siden første er nullte)

$ \binom31= 3 \\ \binom52= 10 \\ \binom83 = 56 $

Oppgave 6

a)

$\frac {2}{3}x^3+x^2-12x+1 \\ f ' (x) = 2x^2+2x-12$

b)

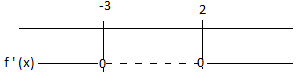
$f ' (x)= 0 \\ 2x^2 + 2x - 12 = 0 \\ x = -3 \vee x=2$

(samme som oppgave 1b)

f er strengt voksende: $x \in <\leftarrow] \cup [2, \rightarrow>$

f er strengt avtagende $x \in [-3, 2]$

Oppgave 7

Tog A; kjører med farten v i t timer. $ v = \frac st \Rightarrow vt =s \Rightarrow vt =120$

Tog B: kjører med en gjennomsnittsfart 20 km/ større enn tog A, altså (v + 20), det bruker da en time mindre enn tog A, altså (t-1). Avstanden er den samme: altså blir (v+20)( t - 1) = 120

<math> \left[ \begin{align*} vt = 120 \\ (v+20)(t-1) = 120 \end{align*}\right] </math>

<math> \left[ \begin{align*} v = \frac{120}t \\ (\frac{120}t +20)(t-1) = 120 \end{align*}\right] </math>

<math> \left[ \begin{align*} 120 - \frac{120}{t} +20t-20 = 120 \end{align*}\right] </math>

<math> \left[ \begin{align*} t^2-t-6=0 \end{align*}\right] </math>

t = 3 timer

Det betyr at tog A holder en gjennomsnittsfart på 40 km/t og tog B 20km/t raskere, altså 60 km/t.

Oppgave 3

a)

b)

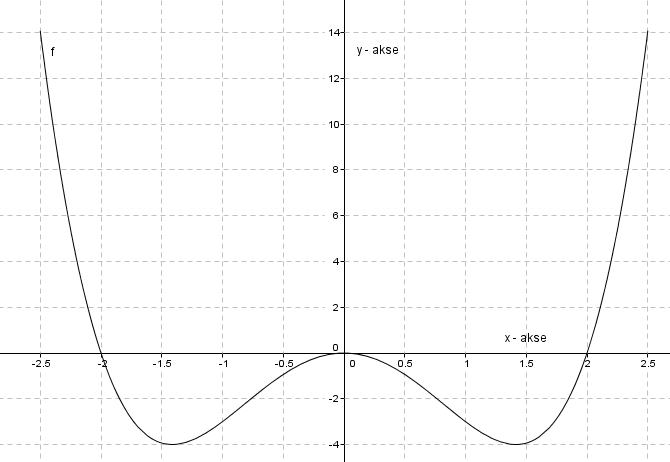
$f(x)= x^4-4x^2\\ f(0)=0$

Altså er skjæring med y-aksen lik null.

$f(x)= 0 \\ x^2(x^2-4) =0 \\ x=0 \vee x^2-4 =0 \\ x=0 \vee x= -2 \vee x=2 $

Nullpunkter: (-2,0), (0, 0) og (2, 0).

c)

$f ' (x)= 4x^3 -8x \\ f' (x)=0 \\ 4x^3 -8x=0 \\ 4x(x^2 -2) = 0 \\ x =0 \vee x = - \sqrt 2 \vee x = \sqrt 2$

Det finnes tre ekstremalpunkter:

$(0, f(0)) = (0,0) \\ (- \sqrt 2, f(-\sqrt 2 ) = (-\sqrt2, -4 )\\ (\sqrt 2, f(\sqrt 2 ) = (\sqrt2, -4 ) $

d)

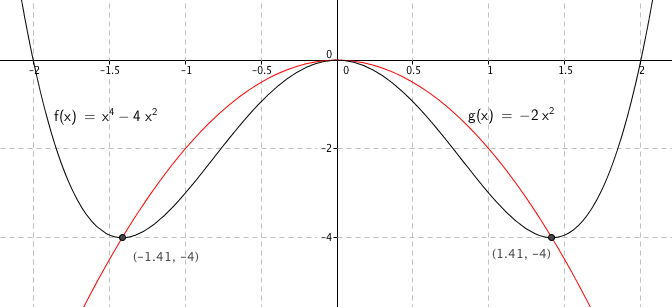
g skal gå gjennom minimumspunktene til f.

$g(x)= ax^2 \\ -4 =a (\pm \sqrt 2)^2 \\ a= -2$

e)