2P 2014 vår LØSNING

oppgaven som pdf

løsning 1 som pdf

løsning 2 som pdf

løsning 2 som LibreOffice Writer fil

løsning 2 GeoGebra-filer og regneark til løsningen

Oppgave 1

2, 5, 8, 10, 10, 15, 22, 28, 40, 50

Skriver tallene opp i stigende rekkefølge med tanke på median. Tall nummer fem er 10 og tall nummer seks er 15. Median bli gjennomsnittet av disse:

$\frac{10+15}{2} = 12,5$

Median er 12,5

Gjennomsnitt: $ \frac{2+5+8+10+10+15+22+28+40+50}{10} = 19$

Gjennomsnittet er 19.

Variasjonsbredden er 50 - 2 = 48.

Oppgave 2

Får tallene på samme form.

$( \frac 23)^2 = \frac 49 \\ (\frac 14)^0 =1 \\ 6 \cdot 2^{-3} = \frac 68 \\ \frac{0,0016}{2\cdot 10^{-3}} = \frac {16}{20} = \frac {8}{10}$

Fra minst til størst blir det: $ \frac 49, \frac 68, \frac {8}{10}, 1$

eller

$( \frac 23)^2 , 6 \cdot 2^{-3},\frac{0,0016}{2\cdot 10^{-3}},(\frac 14)^0 $

Dersom du synes dette er vanskelig å se kan du utvide brøkene slik at alle har samme nevner, da blir telleren avgjørende for størrelsen.

Oppgave 3

5 millioner = 5 000 000 = $5,0 \cdot 10^{6} $

150 milliarder = 150 000 000 000 = $1,5 \cdot 10^{11}$

$ \frac{1,5 \cdot 10^{11}}{5,0 \cdot 10^{6}}$

Oppgave 4

$ \frac{(2x)^4 \cdot 2^{-1}}{8a^2}= \frac{2^4 \cdot a^4 \cdot 2^{-1}}{2^3 \cdot a^2} = 2^{4-1-3} \cdot a^{4-2} = a^2$

Oppgave 5

Man antar at resultatens fordeler seg jevnt utover intervallet i den enkelte klasse.

Poeng	Antall spillere, f	Klassemidtpunkt x	$ x \cdot f $
[0, 40>	60	20	1200
[40, 80>	20	60	1200
[80, 120>	16	100	1600
[120, 180>	4	150	600
Total	100		4600

Gjennomsnitt: $\frac{4600}{100} = 46$

Gjennomsnittet er 46 poeng.

Oppgave 6

Synnøve sykkler 6 km. Det bruker hun 20 munutter på, inkludert en pause på 4 minutter. Først sykkler hun, med jevn fart, 2 kilometer på 6 minutter. Det gir en fart på 20 km/h. (. ganger begge med 10) Hun har pause fra 6 til 10 minutter ute i turen. De siste 10 minuttene sykkler hun 4 km. med jevn hastighet. Om man ganger begge størrelsene med 6 finner man at dette gir en hastighet på 24 km/h.

Oppgave 7

Dette er endel en oppgave og må gjøres med blyant, linjal og gradeskive. Vi har gjort den i Excel for at det skal se litt pent ut.

Det er 60 elever. I en sirkel er det 360 grader. En elev utgjør derfor 360 : 60 = 6 grader. Vi får da følgende tabell:

Oppgave 8

500 liter

2% forsvinner hvert år.

a)

Etter 12 år vil det være igjen:

$Igjen (12 )= 500 \cdot 0,98^{12}$ liter.

b)

Det som har fordampet er forskjellen mellom det som var ved starten, og det som er igjen etter 20 år.

$Fordampet(20)= 500 - 500 \cdot 0,98^{20} $ liter

c)

2% av det som til enhver tid befinner seg på tønnen fordamper hvert år. Det første året fordamper 10 liter, da er det 490 liter igjen. 2% av 490 er mindre enn 10. Slik vil et stadig mindre og mindre volum fordampe, fordi det alltid er 2% av noe som blir mindre og mindre. Det vil være mere på tønna enn 250 liter etter 25 år.

Oppgave 9

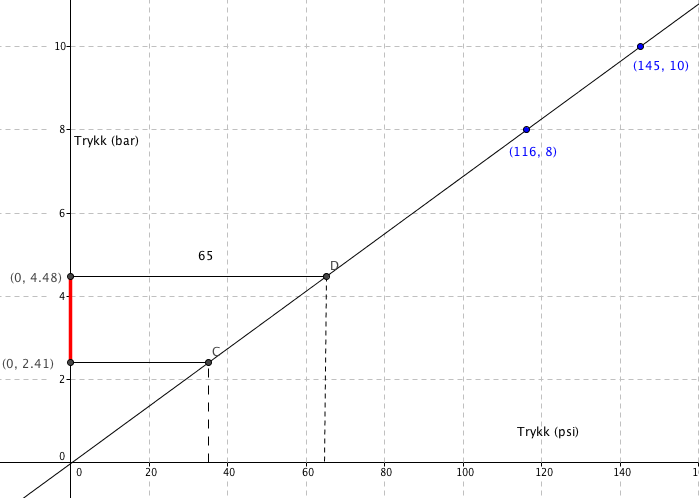
a)

b)

Han bør ha mellom 2,4 og 4,5 bar i dekkene, avhengig av underlaget han skal sykkle på.

Oppgave 1

a)

b)

c)

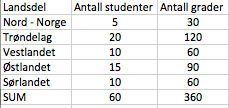
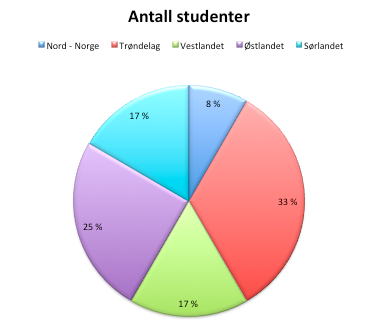
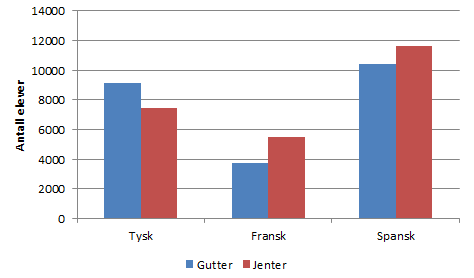
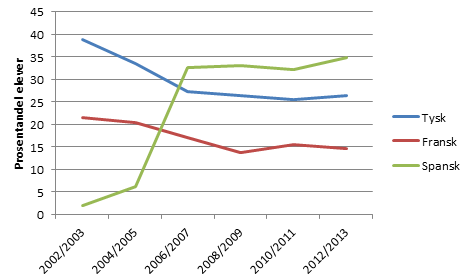
Skoleåret 12 / 13 var det 22004 elever som valgte spansk (10385 + 11619). Det utgjorde 34,9%.

$22004 \cdot \frac{100}{34,9} = 63049$

Det var ca 63049 elever på 8. trinn 2012 / 2013.

Oppgave 2

a)

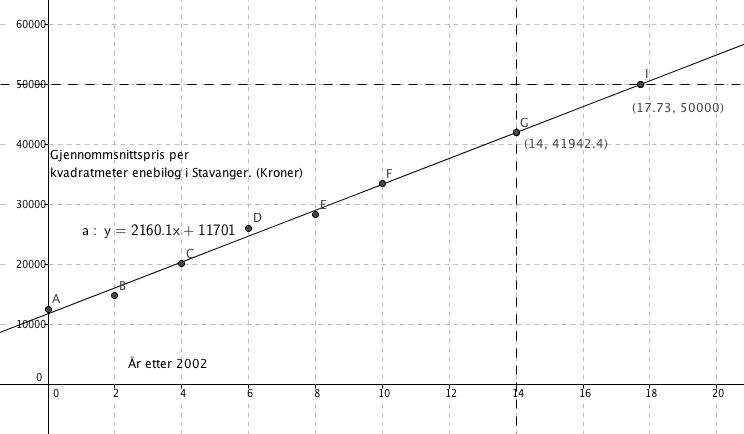
Lineær modell: y = 2160,1x + 11701

b)

Se figur. Gjennomsnittsprisen vil være i underkant a 42 tusen per kvadratmeter, dersom modellen er riktig.

c)

Dersom en bolig på 200 kvadratmeter skal koste 10 millioner tilsvarer det en kvadratmeterpris på 50.000 kroner. Fra figuren i a ser man at det vil skje mot slutten av det 17 året, altså i 2019, forutsatt at utviklingen fortsetter som før.

d)

Dersom økningen over tre år er 20% er økningen per år , forutsatt lik økning hvert år gitt som:

$1 \cdot x^3 = 1,2 \\ x = \sqrt[3] {1,2}\\ x= 1,0627 $

Stigningen per år er ca 6,3%.

Oppgave 3

a)

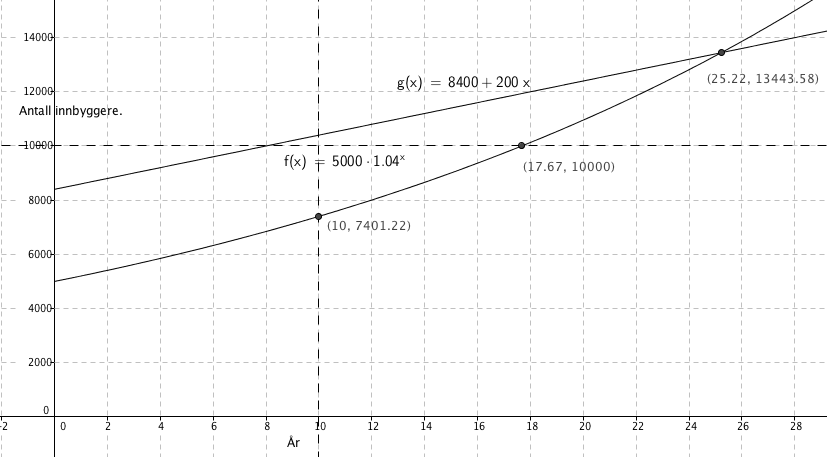
5000 er startverdien. 4% vekst per år tilsvarer en vekstfaktor på 1,04. x er antall perioder, i dette tilfellet år. Modellen er eksponentiell.

b)

c)

Fra Figuren i b ser man at det vil være ca. 7400 innbyggere om 10 år. Innbyggertallet passerer 10000 det 17 åreet.

d)

Modellen for Brimsjø er lieær. Fra figuren over ser man at det vil ta ca 25 år før det er like mange innbyggere begge steder.

Oppgave 4

a)

Omkrets er:

$ 2x+y+(y-20) =120 \\2y = 140-2x \\y=70-x$

Areal:

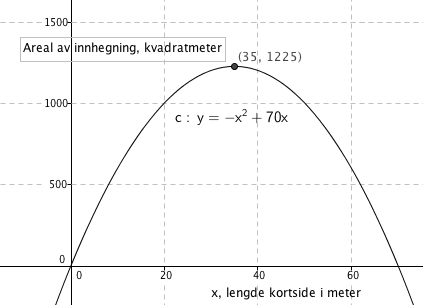
$A(x)= y \cdot x = (70-x)x = 70x-x^2$

b)

Arealet blir størst når x er 35 meter. Da er arealet 1225 kvadratmeter.

Oppgave 5

a)

Gjennomsnittet er summen av alle mål, delt på antall kamper.

$GjS = \frac{6+1+4+8+8+17+7+12+1+8+4+7+10+13+14+7+9+7+11+12+7+4}{22} = \frac{177}{22} \approx 8$

Hun skåret ca. 8 mål per kamp.

b)

Duda har et standardavvik på 4. Hun skårer mere ujevnt, har større spredning på antall mål enn en spiller som har et standardavvik på 2,5. Men fordi hennes gjennomsnitt er 8 mål per kamp vil hun jevnt over skåre flere mål enn den andre spilleren, hvis gjennomsnitt var 5 mål per kamp.

c)

Hun skåret tre mål på straffekast i 21-17 kamper. Dvs i fire kamper skåret hun tre på straffe.

Totalt antall mål på straffe er:$14 \cdot 1 + 3 \cdot 2 + 4 \cdot 3 + 1 \cdot 4 = 36$

Oppgave 6

a)

$F_1 = 1 \\ F_2 = 2+3+2 = 7 \\ F_3 = 3+4+5+4+3 = 19 \\ F_4 = 4+5+6+7+6+5+4 =37 \\F_5 = 5+6+7+8+9 +8+7+6+5 = 61$

b)

Ved å lage små parallellogrammer kan man regne på følgende måte: $F_n = (n-1)^2+ n(n-1)+ n^2 = n^2-2n+1 +n^2-n +n^2 = 3n^2-3n+1$

$F_3 = 3 \cdot 3^2 - 3 \cdot 3 +1 = 19$

$F_5 = 3 \cdot 5^2 - 3 \cdot 5 +1 = 61$

c)

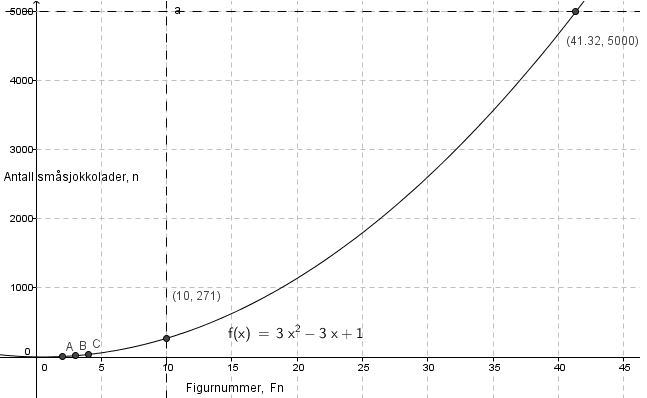
Ved å legge inn F1, F2 og F3 i Geogebra og foreta en polynomregresjon, får man figuren over. Fra figuren ser man at det trengs 271 sjokolader for å lage figur nr. 10.

d)

Fra figuren over ser man at me 5000 sjokolader er det mulig å lage figur nr. 41.