1T 2014 vår LØSNING

Oppgaven som pdf

Tråd om denne oppgaven på Matteprat

Enda en tråd om denne oppgaven på Matteprat

Løsning laget av Nebu

Oppgave 1:

$2,5 \cdot 10^{15} \cdot 3,0 \cdot 10^{-5} = 7,5 \cdot 10^{15+(-5)} = 7,5 \cdot 10^{10}$

Oppgave 2:

$9^{ \frac12}\cdot 6^0 \cdot 4^{-1} \cdot \sqrt[3]{8^2} = \\ (3^2)^{\frac12} \cdot 1 \cdot \frac 14 \cdot \sqrt[3]{2^6} = \\ \frac34 \cdot 2^2 = 3$

Oppgave 3:

$2^{2-x} \cdot 2^{1+2x} =32 \\ 2^{2-x+1+2x} = 2^5 \\ 3+x=5 \\ x=2$

Oppgave 4:

$x^2 +8x +c \\$ Vi har at $a^2 +2ab +b^2 = (a+b)^2$

Dvs: c = $4^2 = 16$

Oppgave 5:

<math> \left[ \begin{align*}2x-3y=-7 \\ 3x-y=7 \end{align*}\right] </math>

<math> \left[ \begin{align*}[ y=3x-7 \\ 2x -3(3x-7) = -7] \end{align*}\right] </math> 2x-9x + 21 = -7 \\ - 7x = - 28 \\ x= 4 \\ 3x-y=7 \\ 12 - y =7 y=5 \\ x = 4 \wedge y = 5$

Oppgave 6:

$\frac {6}{x-3} - \frac {5x+15}{x^2-9}+ 1= \\ \frac{6}{x-3} - \frac {5(x+3)}{(x+3)(x-3)}+ \frac {x-3}{x-3} = \\ \frac {6-5+ x - 3 }{x-3}= \\ \frac {x-2}{x-3}$

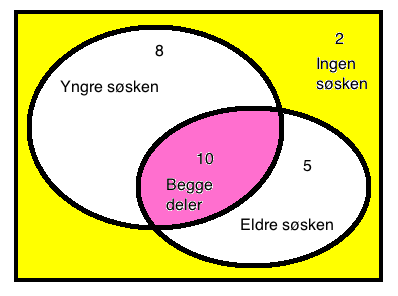
Oppgave 7:

a)

b)

P(eldre men ikke yngre søsken) = $ \frac {5}{25} = \frac 15$

c)

P(yngre søsken gitt eldere søsken) = $\frac {10}{15}= \frac{2}{3}$

Oppgave 9:

$f(x)= x^2+2x-3$

a)

Nullpunkt: $f(x)=0 \\ x^2+2x-3 = 0 \\ x= \frac{-2 \pm \sqrt{4-4 \cdot (-3)}}{2} \\ x= \frac{-2 \pm 4}{2} \\x= -3 \vee x= 1$

Nullpunktene er (-3, 0 ) og (1, 0).

b)

$f´(x) = 2x+2 \\f´(x)=2 \Rightarrow x = 0 $

Tangeringspunkt. ( 0 , f(0) ) som er (0, -3)

Likning for tangenten:

$y = ax+b \\ -3 = 2 \cdot 0 -3 \\ b = -3 \\ y=2x-3$

Den siste utregningen kunne vi sløyfet i dette tilfellet, siden vi vet at tangeringen skjer på y aksen (x = 0).

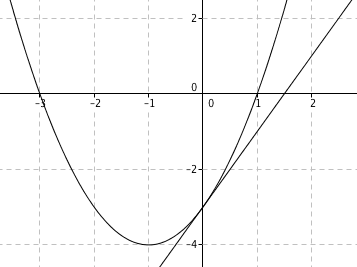
c)

Dette er del en, så du må tegne for hånd. Lag verditabell. Du må også markere hva som er x-akse og y-akse.

Oppgave 10:

$f(x) = x^2+bx+c $

Grafen skjærer y - aksen i (0, 4), dvs. f(0) = 4, altså er c = 4.

Funksjonen f har ett nullpunkt, dvs: $ b^2 - 4ac = 0 \\ b= \pm 4 \\ f(x)= x^2-4x+ 4 \vee f(x)= x^2+ 4x+ 4 $

Oppgave 1

a)

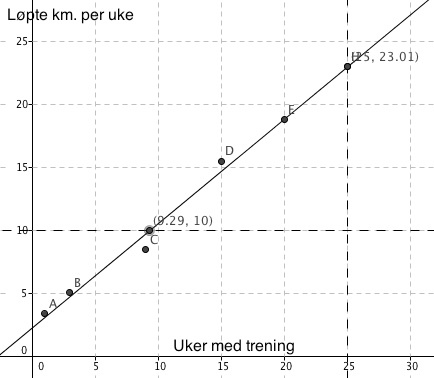
Bruker Geogebra og finner at den lineære funksjonen som passer best med de oppgitte data er :

y = 0,83x + 2,31

x er antall uker etter treningsstart.

b)

Avlesning av Grafen i a gir ca. 23 km.

c)

Avlesning av grafen i a viser at det skjer den niende treningsuken.

Oppgave 2

a)

b)

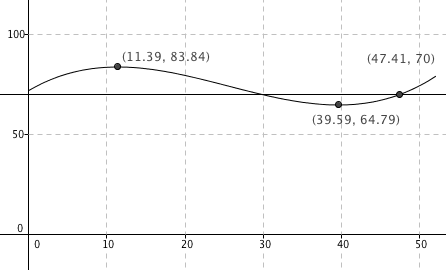
$f(x)=0,0017x^3-0,13x^2+2,3x+72$

Fra funksjonsuttrykket ser man at f (0) = 72. Dvs. han veide 72 kg. den 1. jan 2013.

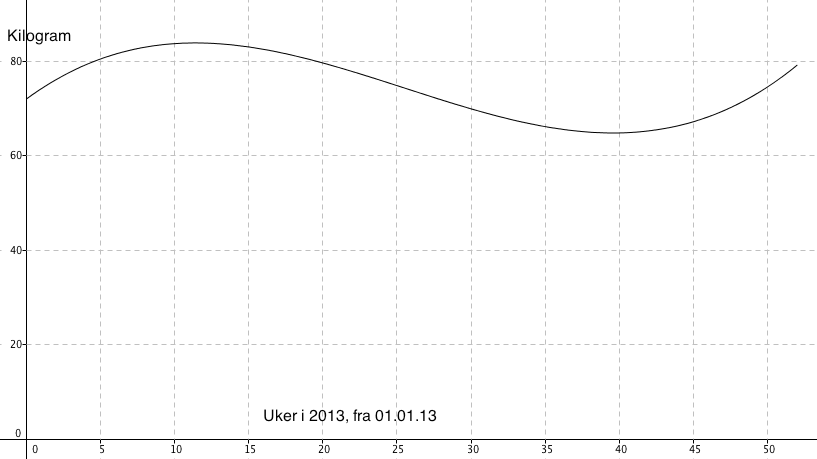
c)

Fra figuren der man at han veide over 70 kg. fra uke 1 til 30 og fra uke 47 til 52, altså ca. 35 uker av året.

d)

Fra Figuren i c ser man at han veide mest i uke 11, nesten 84 kg. Han veide minst i uke 39, da i underkant av 65 kg. Dersom man forholder seg til tallene over er det et vekttap på 19kg. over 28 uker. Det gir et vekttap på ca. 680 gram per uke.

e)

Svarene gir oss den momentane vektendringen i uke 3 og i uke 25.