R1 2013 høst LØSNING: Forskjell mellom sideversjoner
| Linje 105: | Linje 105: | ||
==Oppgave 1== | ==Oppgave 1== | ||
===a)=== | ===a)=== | ||
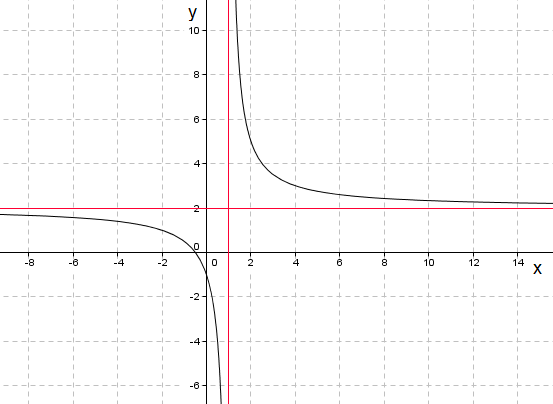
Asymptoter: | |||
Vertikal: $lim_x \to \pm \inf fx)=$ | |||
[[File:2a-r1-h2013.png]] | [[File:2a-r1-h2013.png]] | ||
Sideversjonen fra 7. jan. 2014 kl. 10:12
Matteprat: Diskusjon omkring denne oppgaven
DEL EN
Oppgave 1:
a)
$f(x) = 2e^{3x} \\ f´(x) = 2(3x)´e^{3x} = 6e^{3x}$
b)
$g(x) = 2x \cdot \ln(3x) \\ g´(x) = 2 ln(3x) + 2x \cdot \frac{1}{3x} \cdot (3x)´ \\ g´(x) = 2( \ln(3x)+1)$
c)
$h(x)= \frac {2x-1}{x+1} \\ h´(x) = \frac{2(x+1) - (2x-1)}{(x+1)^2} \\ h´(x) = \frac {3}{(x+1)^2} $
Oppgave 2:
a)
$P(x)= x^3-6x^2+11x-6 \\ P(1)= 1^3 - 6 \cdot 1^2 + 11 \cdot 1 -6 =0$
b)
$ \quad( x^3-6x^2+11x-6) : (x-1) =x^2 - 5x + 6\\ -(x^3 -x^2) \\ \quad \quad -5x^2 \\ \quad \quad -(-5x^2 +5x) \\ \quad \quad \quad \quad \quad \quad 6x-6$
$x^2-5x+6=0 \\ x= \frac{5 \pm \sqrt{25-24}}{2} \\ x= 2 \vee x=3$
$P(x)=x^3-6x^2+11x-6 = (x-1)(x-2)(x-3)$
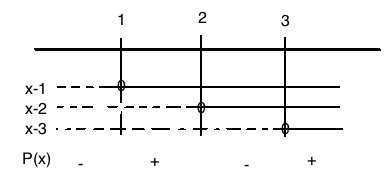
$P(x) \geq 0$
$x \in [1,2] \cup [3, \rightarrow>$
Oppgave 3:
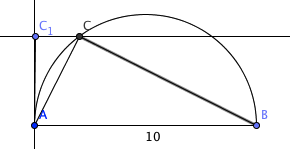
- Avsett linjestykket AB lik 10 cm
- Konstruer en halvsirkel med diameter 10 cm, med sentrum midt mellom A og B.
- Konstruere en linje paralelle med AB, med avstand 4 cm. Denne linjen skjærer halvsirkelen i to punkter.
Oppgave 4:
$2^{3x-1} = 2^2+2^2+2^2+2^2 \\ 2^{3x+1} = 4 \cdot 2^2 \\ 2^{3x-1} = 2^4 \\3x-1 =4 \\ x = \frac 53$
Oppgave 5:
a)
b)
Oppgave 6:
a)
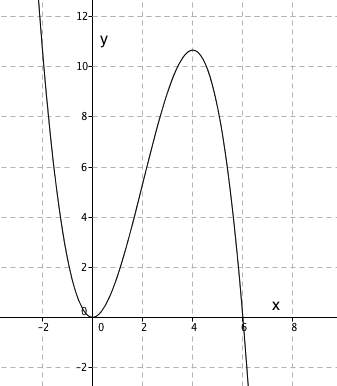
$f(x)= - \frac 13 x^3+2x^2, \quad D_f \in \R \\ f´(x)= -x^2 +4x \\ f´´(x) = -2x+4$
b)
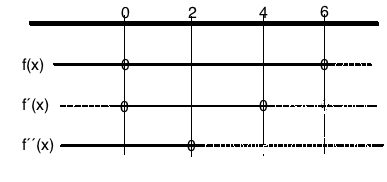
Ekstremalpunkter:
$f ´(x)=0 \\ -x^2+4x=0 \\ x(-x+4)=0 \\ x=0 \vee x= 4 \\ f(0) = 0 \wedge f(4) = \frac{32}{3} \\ (0,0) \wedge ( 4, \frac{32}{3})$
Vendepunkt:
$f´´(x)=0 \\ -2x+4 =0 \\ x= 2 \\ f(2) = - \frac {8}{3} + \frac{24}{3} = \frac {16}{3} \\ (2, \frac{16}{3})$
Fortegnslinjer:
c)
Oppgave 7:
a)
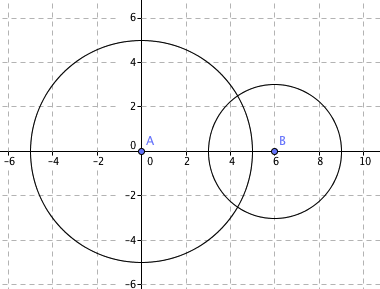
$S_1 : x^2+y^2=25$ Sirkelen har sentrum i origo og radius 5
$S_2 : (x-a)^2+y^2=9$ Setter a=6. Sirkelen har har sentrum i (0,6) og radius 3
b)
$S_2$ kan tangere $S_1$ både utvendig og invendig. Det er bare forskyvning i x rettning, og det finnes fire muligheter.
$a = \pm r_2 \pm r_1 \\ a = \pm 5 \pm 3 \\ a=-8 \vee a= -2 \vee a= 2 \vee a= 8$
DEL TO
Oppgave 1
a)
Asymptoter:
Vertikal: $lim_x \to \pm \inf fx)=$