R1 2013 vår LØSNING: Forskjell mellom sideversjoner
| Linje 87: | Linje 87: | ||
$ \vec c = k \vec a + t \vec b \\ [3, 11] = k[2, 3] + t[-6,4] \\ 3=2k | $ \vec c = k \vec a + t \vec b \\ [3, 11] = k[2, 3] + t[-6,4] \\ 3=2k | ||
- 6t \quad \wedge \quad 11 = 3k +4t \\ k= \frac 32 + 3t \quad \wedge \quad 11= 3( \frac 32 + 3t) + 4t \\ $ | - 6t \quad \wedge \quad 11 = 3k +4t \\ k= \frac 32 + 3t \quad \wedge \quad 11= 3( \frac 32 + 3t) + 4t \\k= \frac 32 + 3t \wedge $ | ||
==Oppgave 8== | ==Oppgave 8== | ||
Sideversjonen fra 3. jan. 2014 kl. 21:03
Løsningsforslag som pdf laget av claes
DEL EN
Oppgave 1
$A(r) = \pi r^2 \\ A'(r) = 2 \pi r \\ V(r) = \frac 43 \pi r^3 \\ V'(r) = 4 \pi r^2$
Oppgave 2
a)
$g(x)=3 \ln(x^2 -1) \\ g'(x)= 3 \cdot \frac{1}{x^2-1} \cdot 2x = \frac{6x}{x^2-1}$
b)
$h(x)= \frac{2x^2}{e^x} \\ h'(x) = \frac{4x \cdot e^x-2x^2e^x}{(e^x)^2} = \frac{2x(2-x)}{e^x}$
Oppgave 3
a)
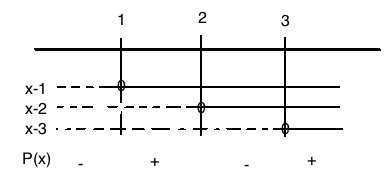
$P(x)= x^3-6x^2+11x-6 \\ P(1)= 1^3 - 6 \cdot 1^2 + 11 \cdot 1 -6 =0$
b)
$ \quad( x^3-6x^2+11x-6) : (x-1) =x^2 - 5x + 6\\ -(x^3 -x^2) \\ \quad \quad -5x^2 \\ \quad \quad -(-5x^2 +5x) \\ \quad \quad \quad \quad \quad \quad 6x-6$
$x^2-5x+6=0 \\ x= \frac{5 \pm \sqrt{25-24}}{2} \\ x= 2 \vee x=3$
$P(x)=x^3-6x^2+11x-6 = (x-1)(x-2)(x-3)$
c)
$P(x) \leq 0$
$x \in < \leftarrow,1] \cup [2,3]$
Oppgave 4
$\ln(a^2b)-2 \ln a - \ln(\frac 1b) \\ = 2 \ln a + \ln b -2 \ln a - \ln 1 + \ln b \\= 2 \ln b$
Oppgave 5
f er kontinuerlig for $x \in <-1, 4>$
f er deriverbar for $x \in <-1, 2> \cup <2,4>$
Oppgave 6
$f(x)= x^3+6x^2-2 \\ f ' (x)= 3x^2 + 12x \\ f ' ' (x) = 6x+12$
vendepunkt;
$f ' ' (x)=0 \\ 6x+12=0 \\x = -2 \\ f(-2) = -8 + 24 -2 = 14 \\ ( -2, 14)$
Vendetangent;
$y= ax+b$
Stigningstall: $f ' (-2)= 3 \cdot 4 +12 \cdot (-2) = -12 $
Tangent:
$ y= -12x +b \\ 14 = -12 \cdot (-2) + b \\ b= 14 - 24 \\ b= -10 \\ y= -12x-10$
Oppgave 7
$\vec a = [2,3], \quad \vec b = [-6, 4], \quad \vec c = [3,11]$
a)
Dersom $ \vec a \perp \vec b$ så er skalarproduktet mellom vektorene lik null.
$[2,3] \cdot [-6,4] = 2 \cdot (-6) + 3 \cdot 4 = -12+12 =0 $ hvilket betyr at vektorene a og b står normalt på hverande.
b)
$ \vec c = k \vec a + t \vec b \\ [3, 11] = k[2, 3] + t[-6,4] \\ 3=2k - 6t \quad \wedge \quad 11 = 3k +4t \\ k= \frac 32 + 3t \quad \wedge \quad 11= 3( \frac 32 + 3t) + 4t \\k= \frac 32 + 3t \wedge $