1T 2012 januar LØSNING: Forskjell mellom sideversjoner
| Linje 171: | Linje 171: | ||
===c)=== | ===c)=== | ||
$ g= \frac{L}{( \frac{T}{2\pi})^2} \\ g= \frac{ | $ g= \frac{L}{( \frac{T}{2\pi})^2} \\ g= \frac{10,0m}{( \frac{6,345 s}{2\pi})^2} =9,806 m/s^2 $ | ||
==Oppgave 8== | ==Oppgave 8== | ||
Sideversjonen fra 29. des. 2013 kl. 19:49
Løsningsforslag laget av Nebu (pdf)
DEL EN
Oppgave 1:
a)
$\frac{x^2-25}{x^2+10x+25} = \frac{(x+5)(x-5)}{(x+5)(x+5)} = \frac{x-5}{x+5}$
b)
$3^{2x-1} = 1 \\ 3^{2x-1} = 3^0 \\ 2x-1 =0 \\ x = \frac 12$
c)
$\frac{a^{\frac 14}\cdot \sqrt a}{(a^{\frac 34})^3 \cdot a^{-2}} = \frac{a^{\frac14} \cdot a^{\frac 12}}{a^{\frac94} \cdot a^{-2}} = a^{\frac14 + \frac 24 - \frac 94 + \frac 84} = a ^{\frac 12} = \sqrt a$
d)
Areal av trekant er: $A = \frac{3 \cdot 4}{2} =6$
Høyden på Figur er h: $A = \frac{gh}{2} \Rightarrow h=\frac{2A}{g} = \frac{2 \cdot 6}{5} = 2,4$
e)
1) $\quad f(x) \leq 0 \quad x \in < \leftarrow, 1] \cup [ 3, \rightarrow>$
2) $\quad fx) > g(x) \quad x \in < \leftarrow, 0 > \cup <5, \rightarrow >$
f)
$ \tan c =\frac{motstående katet}{hosliggende katet} \Rightarrow 2= \frac{3}{AC} \Rightarrow AC = \frac 32$
g)
1) $\quad P(ikke-grønn) = \frac {5}{6} \cdot \frac {4}{5} = \frac 23$
2) $P(en-blå-og-en-rød) = \frac{3}{6} \cdot \frac{2}{5} + \frac{2}{6} \cdot \frac{3}{5} = \frac{12}{30} = \frac 25$
h)
$f(x)=x^2 + 1 \\ f´(x) = lim_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} \\=lim_{\Delta x \rightarrow 0} \frac{(x+ \Delta x)^2+1 - (x^2+1) }{\Delta x} \\ =lim_{\Delta x \rightarrow 0} \frac{x^2+2 x\Delta x + (\Delta x)^2+1 - x^2-1 }{\Delta x} \\ = lim_{\Delta x \rightarrow 0} \frac{2 x\Delta x + (\Delta x)^2 }{\Delta x} \\ =lim_{\Delta x \rightarrow 0} 2 x + \Delta x \\ = 2x$
Oppgave 2
a)
$f(x)= -x^2+2x-2 \\ b^2-4ac = 4 - 4 \cdot 2 = -4$
Siden tallet under rottegnet i abc formelen er negativt har likningen f(x) = 0 ingen løsning og f(x) har ingen nullpunkter.
b)
$f´(x) = -2x+2 \\ f´(x) = 0 \\ -2x+2=0 \\ x= 1 \\f(1) = -1$
Funksjonen har et maksimumspunkt i (1,-1). (Andregradsfunksjoner med negativ faktor forran andregradsleddet har alltid et maksimum).
(dette er del en så du må lage en verditabell og tegne grafen for hånd)
c)
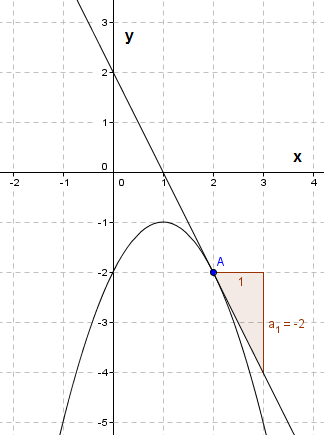
$f´(2) =-2 \\ y =ax + b \\ -2 = -2 \cdot 2 + b \\ b=2 \\ y= -2x + 2$
Finnen først stigningstallet i punktet, ved hjelp av den deriverte. Setter så stigningstallet og verdiene for x og y inn i likningen for den rette linje, for å finne b. Likningen til tangenten i punktet (2, -2) er altså y = -2x + 2.
Oppgave 3
a)
Tilnærmet : F = 2C +30
Nøyaktig: 5F = 9C + 160
$100^{\circ}$ C til Fahrenheit:
Tilnærmet: F= 230
Nøyaktig: 5F = 900 +160, dvs. F= 212
Forskjellen er på 18 Fahrenheit, der den tilnærmede modellen gir for høy verdi.
b)
F= 2C + 30
5F = 9C + 160
10C + 150 = 9C + 160
C=10 og F=50
Den forenklede modellen er mest nøyaktig i området rundt 10 grader Celsius eller 50 Fahrenheit. Akkurat på 40/50 er den forenklede modellen helt nøyaktig.
DEL TO
Oppgave 4
a)
Dersom trekanten er rettvinklet må Pytagoras gjelde og den lengste siden må være hypotenus.
$(6,0 cm)^2 = 36,0 cm^2 \\ (4,0 cm)^2 + (5,0 cm)^2 = 16,0cm^2+25,0cm^2= 41,0cm^2$
Hvilket viser at trekanten ikke er rettvinklet.
b)
Når man kjenner alle sidene i en trekant bruker man cosinussettningen til å finne en vinkel, deretter kan man bryke arealsettningen til å finne arealet av trekanten.
$a^2=b^2+c^2-2ab\cos C \Rightarrow \cos C = \frac{a^2-b^2-c^2}{-2ab}$
c)
Oppgave 5
a)
Sylinder der d + h = 6, d = 2r, og $V = \pi r^2h$. Vi får:
$V= \pi r^2h, \quad setter \quad r=x \\ V= \pi x^2 (6-d) \\ v= \pi x^2 (6 -2x) \\ V= 6 \pi x^2 - 2 \pi x^3, \quad x \in <0,3>$
b)
$V´(x)= 12 \pi x - 6 \pi x^2 \\ V´(x)=0 \\ 12 \pi x -6 \pi x^2 =0 \\ x= 0 \vee x=2$
x=2 gir maksimum volum (x = 0 gir ikke noe volum i det hele tatt)
$V(2) = \pi \cdot 2^2(6-2 \cdot 2) \\ V(2) = 8 \pi$
Oppgave 6
a)
1) 6000 liter var i tanken til å begyne med.
2) Vekstfaktoren er 0,864. Det betyr at det minker med:1,000 - 0,864 = 0,136 = 13,6% per time.
b)
c)
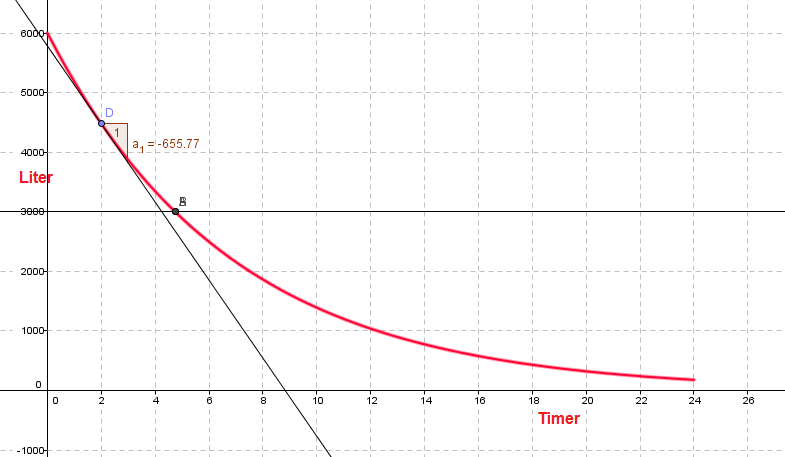
Det tar ca. 4,7 time før halvparten har lekket ut.
d)
Etter to timer tømmes tanken med en fart på 656 liter per time. Vi observerer at denne farten reduseres med tiden, tangenten til grafen blir mindre bratt ettersom tiden går.
Oppgave 7
a)
$T = 2 \pi \sqrt{\frac Lg} \\ \sqrt{\frac Lg} = \frac{T}{2\pi} \\ L = g( \frac{T}{2\pi})^2 $
b)
$ L = g( \frac{T}{2\pi})^2 \\ L = 9,81( \frac{1,0}{2\pi})^2 =24,85 cm$
g er tyngdens aksjerasjon og har benevning meter per sekund i andre, dvs benevningen stemmer her.
c)
$ g= \frac{L}{( \frac{T}{2\pi})^2} \\ g= \frac{10,0m}{( \frac{6,345 s}{2\pi})^2} =9,806 m/s^2 $
Oppgave 8
a)
P(Sørtrøndelag)= $\frac{300000}{5000000} = \frac{3}{50} = 6,0$ %
b)
Dette er egentlig en hypergeometrisk situasjon, men fordi vi tar en liten stikkprøve fra et stort utvag er det mulig å tenke at sannsynligheten er den samme i alle delforsøk (nesten). Man kan derfor regne binomisk.
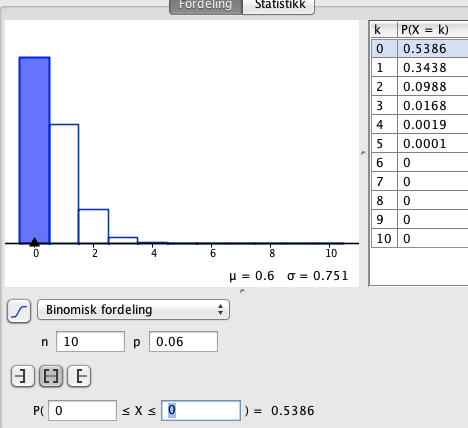
c)
Det er ca 54 % sannsynlig at ingen av de 10 er fra Sørtrøndelag.
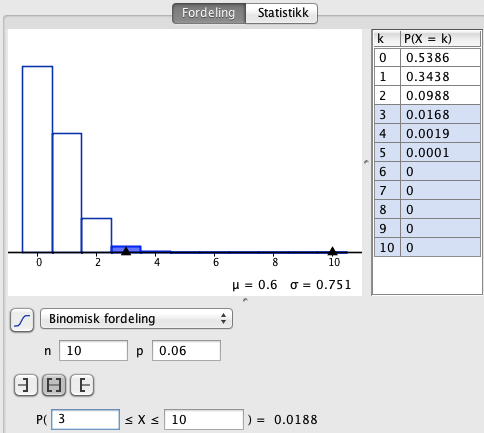
d)
Det er ca. 1,88% sannsynlig at tre eller flere er fra Sørtrøndelag
Oppgave 9
a)
$f(x)= a(x-b)^2+c \\ f(x)=ax^2 -2abx +ab^2 +c$
Ett nullpunkt får man når det er null under rottegnet i abc formelen.
$(-2ab)^2-4a(ab^2+c)=0 \\ 4a^2b^2 - 4a^2b^2 -4ac=0 \\ -4ac=0 \\ c=0$
b)
$f´(x)=2ax-2ab\\ f´(3) =0 \\ 2a \cdot 3 - 2ab =0 \\ 6a = 2ab \\ b=3 $