1P 2012 høst LØSNING

DEL EN

Oppgave 1

Butikk A : $ 2 \cdot 50kr =100kr. \quad$ I butikk A koster druene 100 kroner. (Du betaler for to beger = en kg, og får siste beger "gratis").

Butikk B: $1,5 \cdot 70kr = 105kr. \quad$ I butikk B koster druene 105 kr. Butikk A er billigst.

Oppgave 2

En vare som kostet 50 kr. koster nå 90 kr. Økningen er på 40 kr. Økningen i prosent er:

$ \frac{40 \cdot 100 }{50} = 80$%

Oppgave 3

a)

Antall elever	5	10	30
Pris per elev (kr.)	600 kr	300 kr	100 kr

b)

Det koster $ 5 \cdot 600kr = 3000kr \quad $ å leie hytta.

Oppgave 4

$ 20L = 20 dm^3 = 0,020 m^3 $

4,4h = 4 timer og $0,4 \cdot 60$ min = 4 timer og 24 minutter

200 m/s = 200 m/s $\cdot$ 3600 s = 720 000 m/time = 720 km/h

Oppgave 5

$ \frac{2 \cdot 100}{40} = 5$%

En ökning på 2 prosentpoeng, fra 40% til 42%, tilsvarer en økning på 5%.

Oppgave 6

I basisåret er indeksen 100. For å ha samme kjøpekraft må lønnsutviklingen følge indeksen:

$\frac{500000kr}{100} = \frac{x}{120} \\ 100x = 60000000kr \\ x= 600000kr$

Hun må tjene 600 000 kr for å ha samme kjøpekraft.

Oppgave 7

a)

	Int. Eng	Ikke Int. Eng.	TOTAL
Sos. kun.	5	9	14
Ikke Sos. kun.	7	4	11
TOTAL	12	13	25

b)

5 har valgt begge deler. Av 25 elever blir det: $ \frac{5}{25} = \frac 15 $

c)

Vi vet at eleven har valgt sos.kun. Av disse 14 har 5 valgt int. eng. Vi får: $ \frac{5}{14}$

Oppgave 8

Ett Pund er 4 Litas. Fire Litas ganges med 2,25 og gir 9 NOK (Norske kroner). Ett pund tilsvarer altså 9 NOK.

Oppgave 9

Trekanten er likebeint.

a)

$\angle B = 48,2^{\circ} \\ \angle C = 180^{\circ} - 48,2^{\circ} -48,2^{\circ} = 83,6^{\circ}$

Påstanden i a er riktig.

b)

Vi er på del en og har ikke kalkulator. Høyden fra C på linjestykket AB finner vi ved å bruke Pytagoras:

Høyde: $\sqrt{6^2-4^2} = \sqrt{20} $

Areal trekant: $A= \frac{g \cdot h}{2} = 4 \cdot \sqrt{20}$

Dersom arealet skal bli 20 må høyden være lik 5. Kvadratroten av 20 er mindre enn 5 siden kvadratroten av 25 er 5. Arealet av trekanten er derfor mindre enn 20 og påstanden er sann.

Oppgave 10

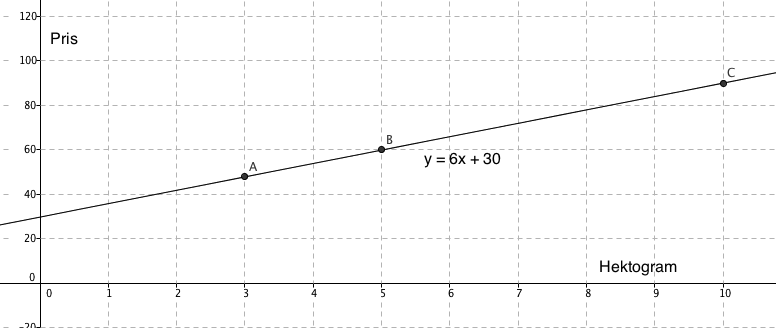
a)

b)

Det ser ut som om grafen krysser y aksen i 30, dvs. et tomt påskeegg koster 30 kr. Fra 0 til 10 hektogram stiger prisen med 60 kroner. Det betyr at et hektogram koster 6 kroner. Funksjonsutrykket blir: y = 6x + 30, der x er antall hektogram, og y er prisen man betaler.

c)

Setter y = 81 i likningen i b, og løser den:

$ y=6x+30 \\ 81 = 6x + 30 \\ 6x = 51 \\ x = \frac{51}{6} \\ x= 8,5$

Man får 8,5 hektogram smågodt for 81 kroner.

DEL TO

Oppgave 1

Ordinær lønn: $90kr \cdot 150 = 13500 kr$

Overtid: $ 90kr \cdot 1,6 \cdot 10 = 1440 kr$

Lønn : 14940 kr.

Skatt:$14940 kr \cdot 0,18 =2689,20kr$

Han betaler 2689,20 kr i skatt.

Oppgave 2

$12000kr \cdot 1,045^{15} = 23223,40kr$

Etter femten år står det 23.223,40 kr på kontoen.

Oppgave 3

a)

Arealet av grunnflaten er: $grunnflate = 14m \cdot 7 m + 1m \cdot 4m =102 m^2$

Arealet av sålen, det lyseblå arealet er $13,5m \cdot 6,5m + 1m \cdot 3,5m = 91,25 m^2$

Areale av grunnmur er areal av grunnflate minus areal av såle: $Grunnmur = 102m^2 . 91,25 m^2 = 10,75m^2$

b)

Volum. $91,25m^2 \cdot 0,1m + 10,75m^2 \cdot 0,4m = 13,425 m^3$

Han trenger 13,4 kubikkmeter betong.

Oppgave 4

a)

$\frac{I_{2010}}{I_{1989}} = \frac{177,2}{68,6} = 2,59$

En vekstfaktor på 2,59 tilsvarer 159% økning.

b)

Indeksen øker med 39,7% i perioden. Dersom boligen følger indeksen blir verdien i 2006: $1700000 \cdot 1,397 = 2374900$

Verdien er ca 2 375 000 i 2006,

c)

Dersom boligen følger indeksen blir verdien i 2010: $1700000 \cdot 1,772 = 3012400$

Prisen de betalte for boligen i 2000 tilsvarer ca 3 mil. i 2010 kroner. Gevinsten er derfor ca. 400.000 kr.

Oppgave 5

	Pizza	Pølse	TOTAL
Salat	$0,75 \cdot 0,5 = 0,375$	0,2	0,7
Ikke Salat	7	4	0,25
TOTAL	0,75	0,25	1