2P 2011 vår LØSNING: Forskjell mellom sideversjoner
| Linje 115: | Linje 115: | ||
</tr> | </tr> | ||
</table> | </table> | ||
[[File:1e-2p-v2011.png]] | |||
=== f) === | === f) === | ||
Sideversjonen fra 19. aug. 2013 kl. 20:42
MAT 1015
Del 1
Oppgave 1
a)
1) <math> 36 200 = 3.62 \cdot 10^4 </math>
2) <math> 0.000 642 = 6.42 \cdot 10^{-4} </math>
3) <math> 53 \text{ millioner} = 5.3 \cdot 10^7 </math>
4) <math> 0.034 \cdot 10^{-2} = 3.4 \cdot 10^{-4} </math>
b)
| Prosentvis endring | Vekstfaktor |
| + 2% | 1 + 0,02 = 1,02 |
| - 68 % | 1-0,68 = 0,32 |
| -75% | 0,25 |
| + 100% | 2 |
c)
1) <math>a^4 \cdot \big( a^2 \big)^{-3} \cdot a^0 = a^4 \cdot a^{2 \cdot (-3)} \cdot a^0 = a^4 \cdot a^{-6} \cdot a^0 = a^{4 - 6 + 0} = a^{-2}</math>
2) <math>\frac{2^{-3} \cdot 4^3 } {8^2} = \frac{2^{-3} \cdot (2^2)^3 } {(2^3)^2} = \frac{2^{-3} \cdot 2^6 } {2^6} = 2^{-3} = \frac{1}{8} </math>
d)
0, 0, 2, 2, 2, 3, 4, 5, 5, 5
1)
Median = <Math>\frac {2+3}{2} = 2,5</Math>
Gjennomsnitt = <Math>\frac {2+2+2+3+4+5+5+5}{10} = 2,8</Math>
2)
| Antall Mål | Frekvens | Kumulativ Frekvens |
| 0 | 2 | 2 |
| 1 | 0 | 2 |
| 2 | 3 | 5 |
| 3 | 1 | 6 |
| 4 | 1 | 7 |
| 5 | 3 | 10 |
3) Den kumulative frekvensen for to mål er fem. Det betyr at i fem av kampene ble det skåret to mål eller mindre.
e)
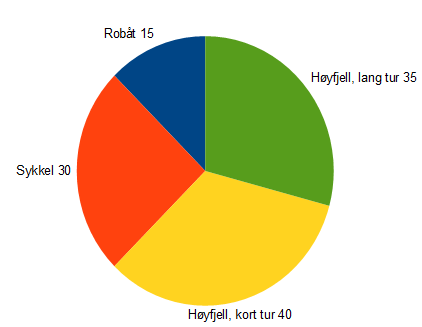
| TUR | Antall elever | Gradetall, sektor |
| Robåt | 15 | $ \frac{15 \cdot 360^{\circ}}{120} = 45^{\circ}$ |
| Sykkel | 30 | $ \frac{30 \cdot 360^{\circ}}{120} = 90^{\circ}$ |
| Høyfjell, kort løype | 40 | $ \frac{40 \cdot 360^{\circ}}{120} = 120^{\circ}$ |
| Høyfjell, lang løype | 35 | $ \frac{35 \cdot 360^{\circ}}{120} = 105^{\circ}$ |
f)
Oppgave 2
a)
b)
c)
Del 2
Oppgave 3
a)
1)
2)
b)
1)
2)
c)
Oppgave 4
a)
b)
c)
d)
e)
Oppgave 5
a)
b)
1)
2)
c)
d)
Oppgave 6
a)
b)
c)
Oppgave 7
a)
1)
2)