1P 2013 vår LØSNING

Diskusjon omkring denne oppgaven

Mer diskusjon omkring denne oppgaven

Del 1

Oppgave 8

a)

Antall kuler: $5$

Antall røde kuler: $3$

Antall blå kuler: $5-3=2$

$P(\text{to røde kuler}) = \frac{3}{5} \cdot \frac{2}{4} = \frac{3 \cdot 2}{5 \cdot 4} = \frac{6}{20} = \frac{3}{10}= 0.3$

Sannsynligheten for å trekke to røde kuler er $0.3$

b)

$P(\text{trekker to røde kuler}) = 0.3$ (fra deloppgave a)

$P(\text{trekker to blå kuler}) = \frac{2}{5} \cdot \frac{1}{4} = \frac{2 \cdot 1}{5 \cdot 4} = \frac{2}{20} = \frac{1}{10}= 0.1$

$P(\text{trekker to kuler i samme farge}) = P(\text{trekker to røde kuler}) + P(\text{trekker to blå kuler}) = 0,3 + 0,1 = 0,4$

Sannsynligheten for at de to kulene han trekker har samme farge er $0,4 = 40\%$

Del 2

Oppgave 2

a)

$P(\text{taco til middag}) = \frac{18}{30} = \frac{3}{5} = 0,6$

b)

$P(\text{taco til middag og marsipankake til dessert}) = P(\text{taco til middag}) \cdot P(\text{marsipankake til dessert}) = \frac{18}{30} \cdot \frac{24}{30} = \frac{12}{25} = 0,48$

c)

	Taco	Pizza	Totalt
Sjokoladekake	2	4	6
Marsipankake	16	8	24
Totalt	18	12	30

$P(\text{taco og marsipankake}) = \frac{16}{30} = \frac{8}{15} = 0.53$

Oppgave 4

a)

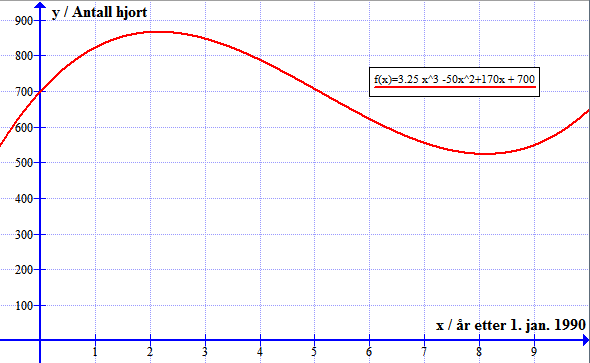
Bruker programmet Graph for å tegne grafen.

Framgangsmåte: Funksjon => sett inn funksjon

b)

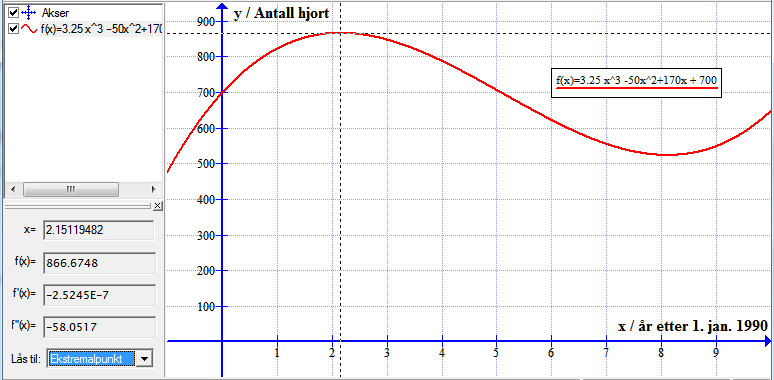
Framgangsmåte: Beregn => Beregn => Lås til ekstremalpunkt => klikk på grafen

Ser at grafen har et toppunkt i $t = 2.15$.

Hjortebestanden var størst i februar 1992. Da var bestanden på 867 dyr.

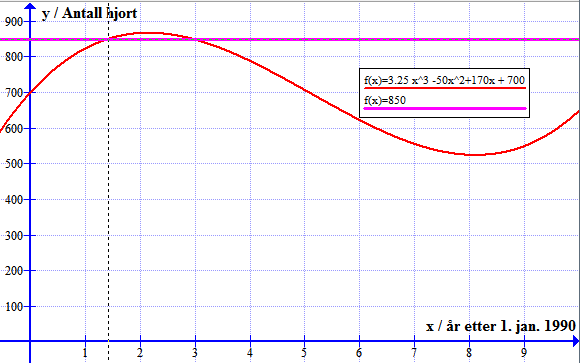
c) Framgangsmåte: Setter inn funksjonen f(t) = 850. Velger Beregn => Beregn => Lås til skjæringspunkt => klikker på grafen

Ser at vi har skjæringspunkt i $t=1,4$ og $t = 2,9$

Løsningen sier at hjortebestanden var på 850 dyr etter mai 1991 og november 1992.

d)

Leser ut av grafen at i $1994$ ($t =4$) er bestanden $788$ hjort. I $1998$ er bestanden $524$ hjort.

Antall år: $1998 - 1994 = 4 $

Endring i antall hjort: $788 - 524 = 264$

Endring per år: $\frac {264}{4} = 66$

Bestanden av hjort minsker i gjennomsnitt med 66 dyr per år i perioden $1994$ til $1998$.