Trekanter: Forskjell mellom sideversjoner
m Teksterstatting – «</tex>» til «</math>» |
|||
| (4 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
| Linje 27: | Linje 11: | ||
En rettvinklet trekant består av to kateter og en hypotenus. Begge katetene vil alltid utgjøre vinkelbeina i den rette vinkelen. Hypotenusen vil alltid være den lengste siden i trekanten. | En rettvinklet trekant består av to kateter og en hypotenus. Begge katetene vil alltid utgjøre vinkelbeina i den rette vinkelen. Hypotenusen vil alltid være den lengste siden i trekanten. | ||
De to katetene < | De to katetene <math>k_1</math> og <math>k_2</math> og hypotenusen <math>h</math> er relatert ved pythagorassetningen: | ||
< | <math>k_1^2+k_2^2=h^2</math> | ||
== Likebeint Trekant == | == Likebeint Trekant == | ||
| Linje 50: | Linje 34: | ||
== Stompvinklet trekant == | == Stompvinklet trekant == | ||
En stompvinklet trekant har en vinkel som er større enn nitti grader. | |||
== Omsenter == | == Omsenter == | ||
[[Bilde:omsenter.png]] | [[Bilde:omsenter.png]] | ||
| Linje 76: | Linje 61: | ||
[[Fil:Cevas.png]] | [[Fil:Cevas.png]] | ||
<p></p> | <p></p> | ||
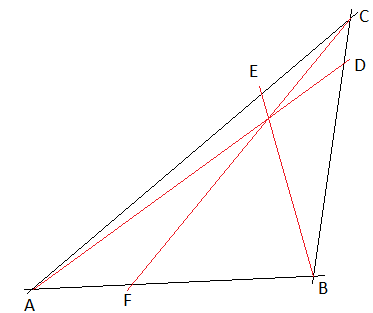
Man har en tifeldig trekant ABC. Man merker av punktene D på BC, E på AC og F på AB. Linjen AD, BE og CF vil møtes i ett punkt | Man har en tifeldig trekant ABC. Man merker av punktene D på BC, E på AC og F på AB. Linjen AD, BE og CF vil møtes i ett punkt hvis og bare hvis (ekvivalens) følgende relasjon er oppfylt:<p></p> | ||
<math>\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1</math> | |||
[[Kategori:Geometri]] | [[Kategori:Geometri]] | ||
Siste sideversjon per 5. feb. 2013 kl. 20:59
Rettvinklet Trekant
En rettvinklet trekant består av to kateter og en hypotenus. Begge katetene vil alltid utgjøre vinkelbeina i den rette vinkelen. Hypotenusen vil alltid være den lengste siden i trekanten.
De to katetene
Likebeint Trekant
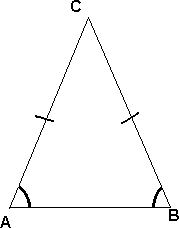
Dersom to av sidene i en trekant er like lange er trekanten likebeint. "Pinnene" på sidene AC og BC markerer at disse sidene er like lange. Når to sider i en trekant er like lange medfører det at to vinkler er like store. I dette eksempelet er vinkel A og vinkel B like store.
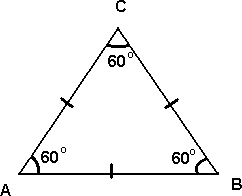
Likesidet Trekant
I en likesidet trekant er alle sidene like lange og alle vinklene er 60°. Legg merke til at dersom man halverer en av sidene i trekanten dannes to trekanter som begge er 30°, 60° og 90°. Dette bør man huske fordi det er nyttig i mange sammenhenger.
Stompvinklet trekant
En stompvinklet trekant har en vinkel som er større enn nitti grader.
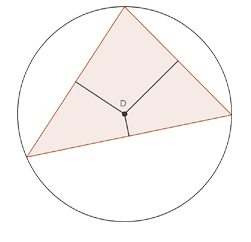
Omsenter
Midtnormalene på sidene i en trekant møtes i et punkt. Dette punktet er sammenfallende med sentrum i den omskrevne sirkelen til trekanten, og kalles for omsenter.
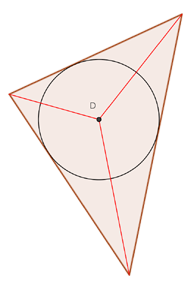
Innsenter
Vinkelhalveringslinjene i en trekant skjærer hverandre i et punkt. Dette punktet er sammenfallende med sentrum i sirkelen innskrevet i trekanten. Punktet kalles trekantens innsenter.
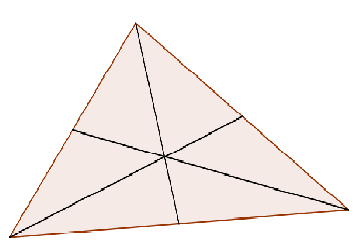
Tyngdepunkt
En median er en linje fra et hjørne i trekanten, til midtpunktet på motstående side. Når man trekker alle tre medianene vil disse skjære hverandre i trekantens tyngdepunkt.
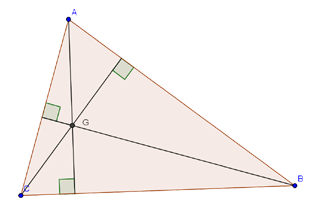
Ortosenter
Punktet der høydene i trekanten møtes kalles ortosenteret.
Cevas setning
Man har en tifeldig trekant ABC. Man merker av punktene D på BC, E på AC og F på AB. Linjen AD, BE og CF vil møtes i ett punkt hvis og bare hvis (ekvivalens) følgende relasjon er oppfylt: