R1 2008 vår LØSNING: Forskjell mellom sideversjoner
| (97 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
==Andre løsninger== | |||
[http://udl.no/matematikk/eksamen-r1-v08 Videoløsning av noen oppgaver fra UDL.no] | |||
= Del 1 = | = Del 1 = | ||
| Linje 6: | Linje 9: | ||
=== a) === | === a) === | ||
< | <math>f(x) = x^2 \cdot lnx \ f'(x) = 2x \cdot lnx + \frac 1x \cdot x^2 = 2xlnx+x = (2lnx+1)x</math> | ||
=== b) === | === b) === | ||
< | <math>\quad(x^3-4x^2+x+6):(x-2) =x^2 -2x - 3 \ -(x^3-2x^2)\ \quad \quad \quad -2x^2+x \ \quad \quad -(-2x^2+4x) \ \quad \quad \quad \quad\quad\quad \quad -3x+6 \ \quad \quad \quad\quad \quad \quad -(-3x+6)\ \quad \quad \quad\quad \quad \quad \quad\quad \quad \quad \quad0</math> | ||
=== c) === | === c) === | ||
< | <math>\lim_{x\to 8} \frac{x^2-64}{2x+16} =\lim_{x\to 8} \frac{(x-8)(x+8)}{2(x-8)}= \lim_{x\to 8} \frac{(x+8)}{2}=8 </math> | ||
=== d) === | === d) === | ||
< | <math>lg(x \cdot y^2)-2lgy+ lg(\frac{x}{y^2}) = \lg x + 2\lg y - 2\lg y +\lg x - 2\lg y = 2(\lg x - \lg y)= 2\lg ( \frac xy)</math> | ||
=== e) === | === e) === | ||
| Linje 22: | Linje 25: | ||
'''1)''' | '''1)''' | ||
'''2)''' | '''2)''' | ||
<Math> f''(x) = (x-2)e^{-x}\ f''(x)=0 \Rightarrow x=2 \ \text{Vendepunkt:}\quad(2,f(2)) = (2,2e^{-2}) = (2, \frac{2}{e^2}) </Math> | |||
== Oppgave 2 == | == Oppgave 2 == | ||
| Linje 29: | Linje 35: | ||
=== a) === | === a) === | ||
Dersom vektorene står vinkelrett på hverandre er skalarproduktet null:<p></p> | |||
=== b) === | |||
== | $l: \begin{bmatrix} | ||
x=3- t \ | |||
y=4 +4 t | |||
\end{bmatrix}$ | |||
<p></p> | |||
Linjen | |||
Hvilket betyr at l er en parameterfremmstilling for | |||
=== c) === | === c) === | ||
Linjen | |||
$l: \begin{bmatrix} | |||
x= 1+ 3s \ | |||
y=2s | |||
\end{bmatrix}$ | |||
=== d) === | === d) === | ||
$l: \begin{bmatrix} | |||
l = m \ | |||
3-t = 1+3s \wedge 4+4t = 2s \ | |||
s = 2 + 2t \wedge 3-t = 1 + 6 + 6t \ | |||
t = - \frac 47 | |||
\end{bmatrix}$ | |||
<p></p> Skjæringspunkt blir da:<p></p> | |||
=== e) === | === e) === | ||
En parameterfremmstilling for $BF_2: \begin{bmatrix} | |||
x=5-2s \ | |||
y=1 + s | |||
\end{bmatrix}$ | |||
<p></p> | |||
$l: \begin{bmatrix} | |||
5-2s = 3-t \wedge 1+s = 4+4t \ | |||
t= - \frac47 | |||
\end{bmatrix}$ | |||
<p></p> | |||
$l: \begin{bmatrix} | |||
x= 3-t = \frac{25}{7} \ | |||
y = 4+4t = \frac {12}{7} | |||
\end{bmatrix}$ | |||
<p></p> | |||
Høydene i en trekant skjærer hverandre i et punkt, ortosenteret. | |||
= Del 2 = | = Del 2 = | ||
| Linje 50: | Linje 96: | ||
=== a) === | === a) === | ||
Dette er et uordnet utvalg uten tilbakelegging: | |||
<p></p> | |||
=== b) === | === b) === | ||
A: Man får utdelt 5 kort tilfeldig, og alle skal være spar. Det er et uordnet utvalg uten tilbakelegging<p></p> | |||
<p></p> | |||
B: Man får utdelt 5 kort tilfeldig, og alle skal være svarte. Det er et uordnet utvalg uten tilbakelegging<p></p> | |||
<p></p> | |||
=== c) === | === c) === | ||
Man vet at alle kortene på hånden er svarte. Sannsynlighete for at de er spar:<p></p> | |||
<p></p> | |||
Dersom A og B er uavhengige hendelser er <p></p> | |||
Som man ser er det ikke tilfelle her. A og B er avhengige hendelser. | |||
== Oppgave 4 == | == Oppgave 4 == | ||
| Linje 65: | Linje 123: | ||
==== a) ==== | ==== a) ==== | ||
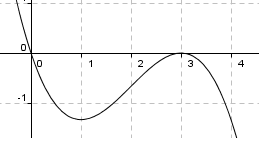
En funksjon vokser når den deriverte er positiv. f vokser for x verdier fra en til tre. | |||
==== b) ==== | ==== b) ==== | ||
f har et minimumspunkt når x = 1, da er den deriverte null og skifter fra negativ til positiv verdi.<p></p> | |||
f har et maksimumspunkt når x = 3, da er den deriverte null og skifter fra positiv til negativ verdi.<p></p> | |||
f har et vendepunkt når x = 2.Den deriverte har et maksimumspunkt, og f skifter fra å vende sin hule side opp, for x verdier mindre enn 2, til å vende sin hule side ned for verdier større enn 2. | |||
==== c) ==== | ==== c) ==== | ||
<math>f'(x) = ax^2+bx+c \ f'(0) = - 3 \Rightarrow c = -3 \ f'(1) = 0 \Rightarrow a+b-3=0 \ x= \frac{-b}{2a} \Rightarrow b = -4a \ a-4a -3 = 0 \Rightarrow a =-1 \quad \wedge \quad b=4 \ | |||
f'(x) = -x^2+4x-3</math> | |||
==== d) ==== | ==== d) ==== | ||
Dersom man deriverer f får man uttrykket for f' gitt i oppgave 4c. f går gjennom origo fordi f(0) = 0. | |||
<p></p>[[Fil:R1-98-4d.png]] | |||
=== Alternativ II === | === Alternativ II === | ||
| Linje 79: | Linje 142: | ||
==== a) ==== | ==== a) ==== | ||
Lengden av DB er | |||
Grunnlinjen i trekanten ABC er 2DB = | |||
Høyden i trekanten ABC er 1+x<p></p> | |||
Arealet av ABC er | |||
==== b) ==== | |||
[[Fil:R1-2012-4.png]] | |||
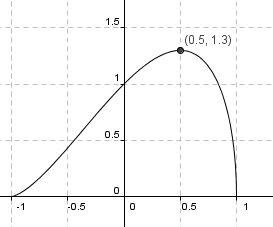
<p></p> Når x=0,5 er arealet 1,3. Dette er det største arealet ABC kan ha. | |||
==== c) ==== | ==== c) ==== | ||
<p></p> | |||
Setter | |||
Dette er i sammsvar med oppgave b, da den deriverte i toppunktet er lik null. | |||
==== d) ==== | |||
==== | Bruker Pytagoras et par ganger: | ||
<math> x= \frac 12 \ DC = \frac 32 \ AB = 2\sqrt{1- \frac 14} = \sqrt3 \AC = BC = \frac{\sqrt{12}}{2} = \sqrt 3</math> | |||
== Oppgave 5 == | == Oppgave 5 == | ||
=== a) === | === a) === | ||
=== b) === | |||
=== c) === | |||
<p></p> | |||
= | <math> (b + c)^2 = (b -c)^2 + (BC)^2 \ (BC)^2 = b^2+2bc+ c^2 -b^2 +2bc - c^2 = 4bc \ BC = 2\sqrt{bc}</math> | ||
=== d) === | === d) === | ||
<math> AC = AB + BC \ 2\sqrt{ab} = 2\sqrt{ac} + 2\sqrt{bc} \ \sqrt{ab} =\sqrt{ac} + \sqrt{bc} \ \frac{\sqrt{ab}}{\sqrt{abc}} = \frac {\sqrt{ac}}{\sqrt{abc}} + \frac{\sqrt{bc}}{\sqrt{abc}} \ | |||
\frac{1}{\sqrt c} = \frac{1}{\sqrt b} + \frac{1}{\sqrt a} | |||
</math> | |||
=== e) === | === e) === | ||
<math> \frac{1}{\sqrt c} = \frac{1}{\sqrt b} + \frac{1}{\sqrt a} \a = b = r \ | |||
\frac{1}{\sqrt c} = \frac{1}{\sqrt r} + \frac{1}{\sqrt r} \ | |||
\frac{1}{\sqrt c} = \frac{2}{\sqrt r}\ 2 \sqrt c = \sqrt r \ c = \frac r4</math> | |||
=== f) === | === f) === | ||
[[Fil:R1-1998-5d.png]] | |||
Siste sideversjon per 26. feb. 2014 kl. 09:43
Andre løsninger
Videoløsning av noen oppgaver fra UDL.no
Del 1
Oppgave 1
a)
b)
c)
d)
e)
1)
2)
<Math> f(x) = (x-2)e^{-x}\ f(x)=0 \Rightarrow x=2 \ \text{Vendepunkt:}\quad(2,f(2)) = (2,2e^{-2}) = (2, \frac{2}{e^2}) </Math>
Oppgave 2
a)
Dersom vektorene står vinkelrett på hverandre er skalarproduktet null:
b)
Linjen
Hvilket betyr at l er en parameterfremmstilling for
c)
Linjen
som gir rettningsvektor [3,2] og parameterfremmstilling:
d)
Skjæringspunkt blir da:
e)
En parameterfremmstilling for
Høydene i en trekant skjærer hverandre i et punkt, ortosenteret.
Del 2
Oppgave 3
a)
Dette er et uordnet utvalg uten tilbakelegging:
b)
A: Man får utdelt 5 kort tilfeldig, og alle skal være spar. Det er et uordnet utvalg uten tilbakelegging
B: Man får utdelt 5 kort tilfeldig, og alle skal være svarte. Det er et uordnet utvalg uten tilbakelegging
c)
Man vet at alle kortene på hånden er svarte. Sannsynlighete for at de er spar:
Dersom A og B er uavhengige hendelser er
Som man ser er det ikke tilfelle her. A og B er avhengige hendelser.
Oppgave 4
Alternativ I
a)
En funksjon vokser når den deriverte er positiv. f vokser for x verdier fra en til tre.
b)
f har et minimumspunkt når x = 1, da er den deriverte null og skifter fra negativ til positiv verdi.
f har et maksimumspunkt når x = 3, da er den deriverte null og skifter fra positiv til negativ verdi.
f har et vendepunkt når x = 2.Den deriverte har et maksimumspunkt, og f skifter fra å vende sin hule side opp, for x verdier mindre enn 2, til å vende sin hule side ned for verdier større enn 2.
c)
d)
Dersom man deriverer f får man uttrykket for f' gitt i oppgave 4c. f går gjennom origo fordi f(0) = 0.
Alternativ II
a)
Lengden av DB er
Grunnlinjen i trekanten ABC er 2DB =
Høyden i trekanten ABC er 1+x
Arealet av ABC er
b)
Når x=0,5 er arealet 1,3. Dette er det største arealet ABC kan ha.
c)
Setter
Dette er i sammsvar med oppgave b, da den deriverte i toppunktet er lik null.
d)
Bruker Pytagoras et par ganger:
Oppgave 5
a)