Asymptote: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
m Teksterstatting – «</tex>» til «</math>» |
||
| (15 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
En rett linje som grafen til f(x) nærmer seg når x går mot en bestemt verdi eller | En rett linje som grafen til f(x) nærmer seg når x går mot en bestemt verdi eller <math> \pm \infty </math>. En graf kan godt krysse en asymptote. Vi har vertikale og horisontale (eller skrå) asymptoter. | ||
[[Bilde: | [[Bilde:hvass.PNG]] | ||
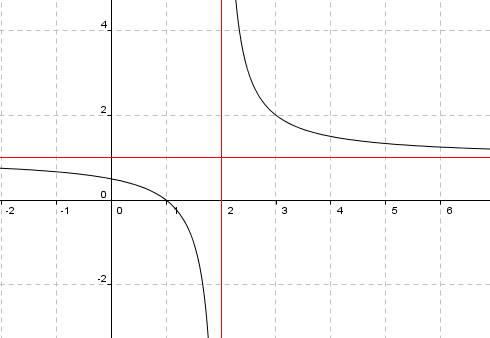
Figuren viser grafen til funksjonen < | Figuren viser grafen til funksjonen <math>f(x)= \frac{x-1}{x-2}</math> | ||
Vi ser at grafen har en vertikal asymptote for x = 2 og en horisontal asymptote for y = 1. | Vi ser at grafen har en vertikal asymptote for x = 2 og en horisontal asymptote for y = 1. | ||
| Linje 14: | Linje 14: | ||
Dersom f (x) går mot pluss / minus uendelig når x nærmer seg et tall a fra den ene eller andre siden (eller begge) så er linjen X = a en vertikal asymptote for f. Dette kan formuleres slik: | Dersom f (x) går mot pluss / minus uendelig når x nærmer seg et tall a fra den ene eller andre siden (eller begge) så er linjen X = a en vertikal asymptote for f. Dette kan formuleres slik: | ||
<math> \lim_{x \to a^+} f(x)= \pm \infty \quad \quad \quad \lim_{x \to a^-} f(x)= \pm \infty </math><p></p> | |||
I eksempelet over er a = 2. | I eksempelet over er a = 2. | ||
== Horisontal (og skrå) asymptote == | == Horisontal (og skrå) asymptote == | ||
For å finne den horisontale asymptoten må vi undersøke hva som skjer med verdien av f (x) når x går mot ± uendelig. Dette skrives slik: | For å finne den horisontale asymptoten må vi undersøke hva som skjer med verdien av f (x) når x går mot ± uendelig. Dette skrives slik: | ||
<math> \lim_{x \to \infty} f(x)= k \quad \quad \quad \lim_{x \to - \infty} f(x)= k </math><p></p> | |||
Dette leses "grenseverdien til f (x) når x går mot pluss / minus uendelig". Dersom et eller begge kriteriene er oppfylt er linjen | Dette leses "grenseverdien til f (x) når x går mot pluss / minus uendelig". Dersom et eller begge kriteriene er oppfylt er linjen y = k en horisontal asymptote for f. | ||
For å kunne se hva f går mot når x går mot ± uendelig kan det være nødvendig å foreta en polynomdivisjon. Dersom f(x)= h(x) | For å kunne se hva f går mot når x går mot ± uendelig kan det være nødvendig å foreta en polynomdivisjon. Dersom <math>f(x)= \frac{h(x)}{g(x)} </math> utfører vi divisjonen. Dersom vi gjør det med eksempelet over ser vi at f (x) kan skrives som <math>f (x) = 1+ \frac{1}{x-2}</math>. Nå ser vi lett at f går mot 1 når x går mot ± uendelig. | ||
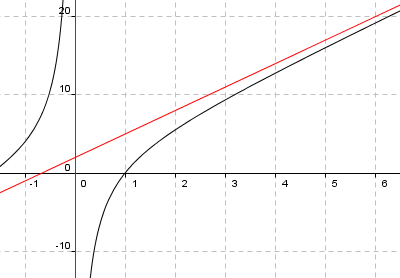
Når teller og nevner er av samme orden blir asymptoten en horisontal linje. Dersom telleren h (x) er en orden over nevneren får vi en skrå asymptote. Dersom vi har funksjonen f (x)= | Når teller og nevner er av samme orden blir asymptoten en horisontal linje. Dersom telleren h (x) er en orden over nevneren får vi en skrå asymptote. Dersom vi har funksjonen <math>f (x)= \frac{3x^2 + 2x -5}{x} </math>og utfører divisjonen ser vi at den kan skrives som <math>f (x)= 3x + 2 - \frac 5x</math>. Vi ser at når x går mot ± uendelig går f mot den rette linjen 3x + 2. Grafen ser slik ut: | ||
[[Bilde:Skra.PNG]] | |||
Siste sideversjon per 5. feb. 2013 kl. 20:58
En rett linje som grafen til f(x) nærmer seg når x går mot en bestemt verdi eller <math> \pm \infty </math>. En graf kan godt krysse en asymptote. Vi har vertikale og horisontale (eller skrå) asymptoter.
Figuren viser grafen til funksjonen <math>f(x)= \frac{x-1}{x-2}</math>
Vi ser at grafen har en vertikal asymptote for x = 2 og en horisontal asymptote for y = 1.
Vertikal asymptote
Dersom f (x) går mot pluss / minus uendelig når x nærmer seg et tall a fra den ene eller andre siden (eller begge) så er linjen X = a en vertikal asymptote for f. Dette kan formuleres slik:
<math> \lim_{x \to a^+} f(x)= \pm \infty \quad \quad \quad \lim_{x \to a^-} f(x)= \pm \infty </math>
I eksempelet over er a = 2.
Horisontal (og skrå) asymptote
For å finne den horisontale asymptoten må vi undersøke hva som skjer med verdien av f (x) når x går mot ± uendelig. Dette skrives slik:
<math> \lim_{x \to \infty} f(x)= k \quad \quad \quad \lim_{x \to - \infty} f(x)= k </math>
Dette leses "grenseverdien til f (x) når x går mot pluss / minus uendelig". Dersom et eller begge kriteriene er oppfylt er linjen y = k en horisontal asymptote for f.
For å kunne se hva f går mot når x går mot ± uendelig kan det være nødvendig å foreta en polynomdivisjon. Dersom <math>f(x)= \frac{h(x)}{g(x)} </math> utfører vi divisjonen. Dersom vi gjør det med eksempelet over ser vi at f (x) kan skrives som <math>f (x) = 1+ \frac{1}{x-2}</math>. Nå ser vi lett at f går mot 1 når x går mot ± uendelig.
Når teller og nevner er av samme orden blir asymptoten en horisontal linje. Dersom telleren h (x) er en orden over nevneren får vi en skrå asymptote. Dersom vi har funksjonen <math>f (x)= \frac{3x^2 + 2x -5}{x} </math>og utfører divisjonen ser vi at den kan skrives som <math>f (x)= 3x + 2 - \frac 5x</math>. Vi ser at når x går mot ± uendelig går f mot den rette linjen 3x + 2. Grafen ser slik ut: