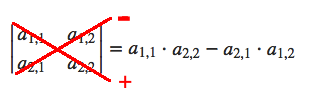Vektorprodukt: Forskjell mellom sideversjoner
| (54 mellomliggende versjoner av 4 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
Vektorproduktet er en operasjon mellom to 3-dimensjonale vektorer som har nyttige anvendelser i blant annet areal- og volumberegninger og når vi skal finne normalvektorer til flater og plan i rommet. Merk at vektorproduktet slik det er definert ikke gir mening for annet enn 3- og 7-dimensjonale vektorer, der vi kun har fokus på det 3-dimensjonale tilfellet. | Vektorproduktet er en operasjon mellom to 3-dimensjonale vektorer som har nyttige anvendelser i blant annet areal- og volumberegninger og når vi skal finne normalvektorer til flater og plan i rommet. Merk at vektorproduktet slik det er definert ikke gir mening for annet enn 3- og 7-dimensjonale vektorer, der vi kun har fokus på det 3-dimensjonale tilfellet. | ||
==Determinanter== | |||
$\begin{vmatrix}a_{1,1} & a_{1,2} \\ | |||
a_{2,1} & a_{2,2} \end{vmatrix} = a_{1,1}\cdot a_{2,2} - a_{2,1} \cdot a_{1,2} \quad \quad $ | |||
[[Bilde:vektor004.png]] | |||
Når man multipliserer diagonalt nedover mot høyre blir fortegnet positivt. Multiplikasjon diagonalt nedover mot venstre gir negativt fortegn. | |||
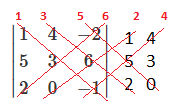
$ \begin{vmatrix}1 & 4 & -2 \\5 & 3 & 6 \\2 & 0 & -1 \end{vmatrix}$ = -3 - 0 + 48 +20 + 0 + 12 = 77 | |||
Vi kom fram til dette på følgende måte: Vi utvider determinaten med to kolonner, slik at kolonne en og to repeteres etter kolonne tre. | |||
[[Bilde:vektor011.png]] | |||
$( 1 \cdot 3 \cdot (-1) - 1 \cdot 6 \cdot 0) + (4 \cdot 6 \cdot 2 - 4 \cdot 5 \cdot(-1)) + ((-2) \cdot 5 \cdot 0 - (-2) \cdot 3 \cdot 2)= -3 -0+48+20+0+12=77 $ | |||
== Definisjon av vektorprodukt (kryssprodukt)== | == Definisjon av vektorprodukt (kryssprodukt)== | ||
Vi bruker notasjonen < | Vi bruker notasjonen <math>\times</math> for vektorprodukt. Lar vi <math>\vec{v_1}=(x_1,y_1,z_1)</math> og <math>\vec{v_2}=(x_2,y_2,z_2)</math> er | ||
:< | :<math>\vec{v_1}\times \vec{v_2}=\left ( y_1z_2-y_2z_1), -(x_1z_2-x_2z_1), (x_1y_2-x_2y_1 \right )</math> | ||
| Linje 14: | Linje 29: | ||
:< | :<math> \vec{v_1}\times\vec{v_2} = \left| \begin{array}{ccc}i & j & k \\x_1 & y_1 & z_1 \\x_2 & y_2 & z_2 \end{array} \right |</math> | ||
Utvikler vi i første rad ser vi at determinanten blir | Utvikler vi i første rad ser vi at determinanten blir | ||
:< | :<math>\vec{v_1}\times\vec{v_2}= (y_1z_2-y_2z_1)i, -(x_1z_2-x_2z_1)j, (x_1y_2-x_2y_1)k</math>. | ||
Her tolker vi <math>i,j,k</math> som enhetsvektorer langs x-,y- og z-aksen, og da ser vi at dette er i overensstemmelse med den første definisjonen. | |||
==Eksempel== | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
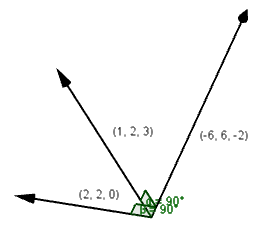
$[1,2,3] x [2,2,0] = \begin{vmatrix}i & j & k \\1 & 2 & 3 \\2 & 2 & 0 \end{vmatrix} = [0-6, 6-0, 2-4] =[-6, 6,-2] $ | |||
[[Bilde:vektor014.png]] | |||
</div> | |||
| Linje 28: | Linje 54: | ||
:< | :<math>\vec{v_2}\times \vec{v_1}=-\vec{v_1}\times \vec{v_2}</math> | ||
== Geometrisk tolkning == | == Geometrisk tolkning == | ||
| Linje 34: | Linje 60: | ||
[[Bilde:480px-Cross product parallelogram.svg.png|right|thumb|Geometrisk bilde av vektorproduktet]] | [[Bilde:480px-Cross product parallelogram.svg.png|right|thumb|Geometrisk bilde av vektorproduktet]] | ||
Vektorproduktet < | Vektorproduktet <math>\vec{v_1}\times \vec{v_2}</math> er en ny vektor, si <math>\vec{v_3}</math>, som står normalt (vinkelrett) på både <math>\vec{v_1}</math> og <math>\vec{v_2}</math> og har lengde <math>|\vec{v_1}||\vec{v_2}|\sin(\theta)</math> der <math>\theta</math> er den minste vinkelen mellom vektorene. Retningen til <math>\vec{v_3}</math> følger høyrehåndsregelen, dvs. at dersom vi tilpasser et slags koordinatsystem slik at <math>\vec{v_1}</math> følger x-aksen i positiv retning og <math>\vec{v_2}</math> følger y-aksen i positiv retning, vil <math>\vec{v_3} </math> peke i positiv retning langs z-aksen. | ||
=== Absoluttverdien av vektorproduktet === | === Absoluttverdien av vektorproduktet === | ||
| Linje 41: | Linje 67: | ||
:< | :<math>|\vec{v_1}\times \vec{v_2}|</math> | ||
| Linje 47: | Linje 73: | ||
:< | :<math>|\vec{v_1}\times \vec{v_2}|=|\vec{v_1}||\vec{v_2}|\sin(\theta)</math> | ||
der < | der <math>\theta</math> er (den minste) vinkelen mellom vektorene. Da ser vi geometrisk at dette er likt arealet av parallellogrammet. For spesialtilfellet <math>\theta=\frac{\pi}{2}</math> vil vektorene utspenne et rektangel, og da ser vi enkelt at arealtolkningen stemmer siden <math>\sin(\frac{\pi}{2})=1</math>. | ||
==Eksempler== | ==Eksempler== | ||
| Linje 59: | Linje 84: | ||
Gitt vektorene < | Gitt vektorene <math>\vec{p}=(1,4,2)</math> og <math>\vec{q}=(9,7,1)</math> beregner vi vektorproduktet som følger: | ||
:< | :<math> \vec{p}\times\vec{q}=(1,4,2)\times (9,7,1)=(4\cdot 1-7\cdot 2, -(1\cdot 1-9\cdot 2),1\cdot 7-9\cdot 4)=(-10,17,-29)</math> | ||
== Høyrehåndsregelen == | == Høyrehåndsregelen == | ||
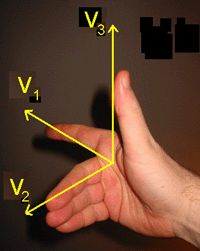
Vi har vektoren < | Vi har vektoren <math>\vec{ v_1}</math> og vektoren <math> \vec{v_2}</math>. Vektorproduktet av de to vektorene vil være en vektor <math>\vec{v_3}</math> som står vinkelrett på planet som inneholder vektoren <math>\vec{v_1}</math> og vektoren <math>\vec{v_2}</math>. | ||
Dersom du bruker høyre hånd og holder pekefingren parallell med < | Dersom du bruker høyre hånd og holder pekefingren parallell med <math>\vec{v_1}</math>, bøy langfingren slik at den er parallell med <math>\vec{v_2}</math> og la tommelfingren stå rett ut fra hånden. Tommelen peker nå i samme retning som <math>\vec{v_3}</math>. Regelen kalles høyrehåndsregelen. | ||
[[Bilde:Haand.gif]] | [[Bilde:Haand.gif]] | ||
== Regneregler == | == Regneregler == | ||
Vektorproduktet skrives < | Vektorproduktet skrives <math> \vec{v_1}\times \vec{v_2}</math> og kalles derfor ofte for kryssproduktet. Operasjoner er ikke kommutativ eller assosiativ. Følgende regneregler gjelder: | ||
<math>\vec{v_1}\times \vec{v_1} = -( \vec{v_2} \times \vec{v_1}) \\ \\ | |||
(\vec{v_1} + \vec{v_2}) \times \vec{v_3} = (\vec{v_1} \times \vec{v_3}) + (\vec{v_2} \times \vec{v_3})\\ \\ | |||
(k\vec{v_1}) \times \vec{v_2} = \vec{v_1} \times (k\vec{v_2})= k(\vec{v_1} \times \vec{v_2})</math> <p></p> | |||
Når man tar skalarproduktet av to vektorer blir resultatet en skalar, eller et tall. Når man tar vektorproduktet blir resultatet en ny vektor. Lengden av denne vektoren er gitt ved: | Når man tar skalarproduktet av to vektorer blir resultatet en skalar, eller et tall. Når man tar vektorproduktet blir resultatet en ny vektor. Lengden av denne vektoren er gitt ved: | ||
| | <math>|\vec{v_1} \times \vec{v_2}| = |\vec{v_1}| \cdot |\vec{v_2}|\cdot \sin \phi, \quad \phi \in [0^{\circ},180^{\circ}]</math>. | ||
== Bruksområder == | |||
Vektorproduktet brukes til å beskrive fenomener i fysikken og det kan også brukes til å regne ut arealer og volumer, samt til å bestemme et plans normalvektor. Eksempelvis har vi at: | |||
=== Arealet at parallellogram === | |||
utspent av vektorene <math>\vec{v_1}</math> og <math>\vec{v_2}</math> er gitt ved | |||
<math>A = |\vec{v_1} \times \vec{v_2}| </math> | |||
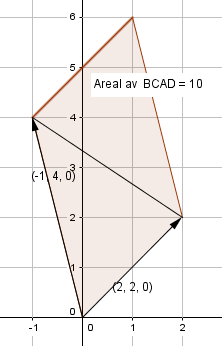
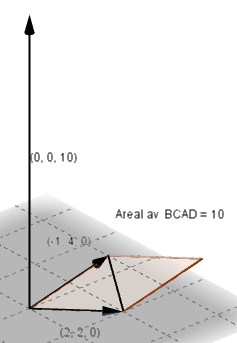
[[Bilde:vektor013.png]] [[Bilde:vektor012.png]] | |||
Vektorene[-1, 4,0] og[2,2,0] ligger begge i xy planet og utspenner et parallellogram med areal 10, se figur til venstre. Ved å ta kryssproduktet får man vektoren [0, 0, 10] som jo er parallel med Z aksen, normalt på de to vektorene i xy planet. Denne vektoren har lengde 10, som jo er sammenfallende med arealet av parallellogrammet. | |||
=== Arealet av en trekant === | |||
utspent av vektorene <math>\vec{v_1}</math> og <math>\vec{v_2}</math> er gitt ved | |||
<math>A = \frac 12\cdot|\vec{v_1} \times \vec{v_2}| </math> | |||
[[Bilde:vektor005.png]] | |||
| Linje 100: | Linje 133: | ||
=== Volumet av en trekantet pyramide === | === Volumet av en trekantet pyramide === | ||
bestemt av vektorene | bestemt av vektorene <math>\vec{v_1}</math>, <math>\vec{v_2}</math> og <math>\vec{v_3}</math> er gitt ved | ||
< | <math>V= \frac 16 \cdot|(\vec{v_1}\times \vec{v_2})\cdot \vec{v_3}|</math> | ||
[[Bilde:vektor007.png]] | |||
=== Volumet av en firkantet pyramide === | === Volumet av en firkantet pyramide === | ||
bestemt av vektorene | bestemt av vektorene <math>\vec{v_1}</math>, <math>\vec{v_2}</math> og <math>\vec{v_3}</math> er gitt ved | ||
< | <math>V= \frac 13 \cdot |(\vec{v_1} \times \vec{ v_2})\cdot \vec{v_3}|</math> | ||
[[Bilde:vektor009.png]] [[Bilde:vektor010.png]] | |||
=== Volumet av et parallellepiped === | |||
bestemt av vektorene <math>\vec{v_1}</math>, <math>\vec{v_2}</math> og <math>\vec{v_3}</math> er gitt ved | |||
<math>V = |(\vec{v_1}\times \vec {v_2})\cdot \vec{v_3}|</math> | |||
[[kategori:lex]] | [[kategori:lex]] | ||
Siste sideversjon per 16. jun. 2020 kl. 18:48
Vektorproduktet er en operasjon mellom to 3-dimensjonale vektorer som har nyttige anvendelser i blant annet areal- og volumberegninger og når vi skal finne normalvektorer til flater og plan i rommet. Merk at vektorproduktet slik det er definert ikke gir mening for annet enn 3- og 7-dimensjonale vektorer, der vi kun har fokus på det 3-dimensjonale tilfellet.
Determinanter
$\begin{vmatrix}a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{vmatrix} = a_{1,1}\cdot a_{2,2} - a_{2,1} \cdot a_{1,2} \quad \quad $
Når man multipliserer diagonalt nedover mot høyre blir fortegnet positivt. Multiplikasjon diagonalt nedover mot venstre gir negativt fortegn.
$ \begin{vmatrix}1 & 4 & -2 \\5 & 3 & 6 \\2 & 0 & -1 \end{vmatrix}$ = -3 - 0 + 48 +20 + 0 + 12 = 77
Vi kom fram til dette på følgende måte: Vi utvider determinaten med to kolonner, slik at kolonne en og to repeteres etter kolonne tre.
$( 1 \cdot 3 \cdot (-1) - 1 \cdot 6 \cdot 0) + (4 \cdot 6 \cdot 2 - 4 \cdot 5 \cdot(-1)) + ((-2) \cdot 5 \cdot 0 - (-2) \cdot 3 \cdot 2)= -3 -0+48+20+0+12=77 $
Definisjon av vektorprodukt (kryssprodukt)
Vi bruker notasjonen <math>\times</math> for vektorprodukt. Lar vi <math>\vec{v_1}=(x_1,y_1,z_1)</math> og <math>\vec{v_2}=(x_2,y_2,z_2)</math> er
- <math>\vec{v_1}\times \vec{v_2}=\left ( y_1z_2-y_2z_1), -(x_1z_2-x_2z_1), (x_1y_2-x_2y_1 \right )</math>
Definisjonen kan også skrives som en determinant som gjør den lettere å huske,
- <math> \vec{v_1}\times\vec{v_2} = \left| \begin{array}{ccc}i & j & k \\x_1 & y_1 & z_1 \\x_2 & y_2 & z_2 \end{array} \right |</math>
Utvikler vi i første rad ser vi at determinanten blir
- <math>\vec{v_1}\times\vec{v_2}= (y_1z_2-y_2z_1)i, -(x_1z_2-x_2z_1)j, (x_1y_2-x_2y_1)k</math>.
Her tolker vi <math>i,j,k</math> som enhetsvektorer langs x-,y- og z-aksen, og da ser vi at dette er i overensstemmelse med den første definisjonen.
Eksempel
$[1,2,3] x [2,2,0] = \begin{vmatrix}i & j & k \\1 & 2 & 3 \\2 & 2 & 0 \end{vmatrix} = [0-6, 6-0, 2-4] =[-6, 6,-2] $
Merk at kryssproduktet ikke er kommutativt. Bruker vi definisjonen ser vi at
- <math>\vec{v_2}\times \vec{v_1}=-\vec{v_1}\times \vec{v_2}</math>
Geometrisk tolkning
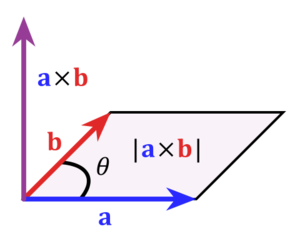
Vektorproduktet <math>\vec{v_1}\times \vec{v_2}</math> er en ny vektor, si <math>\vec{v_3}</math>, som står normalt (vinkelrett) på både <math>\vec{v_1}</math> og <math>\vec{v_2}</math> og har lengde <math>|\vec{v_1}||\vec{v_2}|\sin(\theta)</math> der <math>\theta</math> er den minste vinkelen mellom vektorene. Retningen til <math>\vec{v_3}</math> følger høyrehåndsregelen, dvs. at dersom vi tilpasser et slags koordinatsystem slik at <math>\vec{v_1}</math> følger x-aksen i positiv retning og <math>\vec{v_2}</math> følger y-aksen i positiv retning, vil <math>\vec{v_3} </math> peke i positiv retning langs z-aksen.
Absoluttverdien av vektorproduktet
Absoluttverdien
- <math>|\vec{v_1}\times \vec{v_2}|</math>
er arealet til parallellogrammet utspent av vektorene. Bruker vi definisjonen kan vi vise at
- <math>|\vec{v_1}\times \vec{v_2}|=|\vec{v_1}||\vec{v_2}|\sin(\theta)</math>
der <math>\theta</math> er (den minste) vinkelen mellom vektorene. Da ser vi geometrisk at dette er likt arealet av parallellogrammet. For spesialtilfellet <math>\theta=\frac{\pi}{2}</math> vil vektorene utspenne et rektangel, og da ser vi enkelt at arealtolkningen stemmer siden <math>\sin(\frac{\pi}{2})=1</math>.
Eksempler
Beregning av vektorprodukt
Gitt vektorene <math>\vec{p}=(1,4,2)</math> og <math>\vec{q}=(9,7,1)</math> beregner vi vektorproduktet som følger:
- <math> \vec{p}\times\vec{q}=(1,4,2)\times (9,7,1)=(4\cdot 1-7\cdot 2, -(1\cdot 1-9\cdot 2),1\cdot 7-9\cdot 4)=(-10,17,-29)</math>
Høyrehåndsregelen
Vi har vektoren <math>\vec{ v_1}</math> og vektoren <math> \vec{v_2}</math>. Vektorproduktet av de to vektorene vil være en vektor <math>\vec{v_3}</math> som står vinkelrett på planet som inneholder vektoren <math>\vec{v_1}</math> og vektoren <math>\vec{v_2}</math>.
Dersom du bruker høyre hånd og holder pekefingren parallell med <math>\vec{v_1}</math>, bøy langfingren slik at den er parallell med <math>\vec{v_2}</math> og la tommelfingren stå rett ut fra hånden. Tommelen peker nå i samme retning som <math>\vec{v_3}</math>. Regelen kalles høyrehåndsregelen.
Regneregler
Vektorproduktet skrives <math> \vec{v_1}\times \vec{v_2}</math> og kalles derfor ofte for kryssproduktet. Operasjoner er ikke kommutativ eller assosiativ. Følgende regneregler gjelder:
<math>\vec{v_1}\times \vec{v_1} = -( \vec{v_2} \times \vec{v_1}) \\ \\
(\vec{v_1} + \vec{v_2}) \times \vec{v_3} = (\vec{v_1} \times \vec{v_3}) + (\vec{v_2} \times \vec{v_3})\\ \\
(k\vec{v_1}) \times \vec{v_2} = \vec{v_1} \times (k\vec{v_2})= k(\vec{v_1} \times \vec{v_2})</math>
Når man tar skalarproduktet av to vektorer blir resultatet en skalar, eller et tall. Når man tar vektorproduktet blir resultatet en ny vektor. Lengden av denne vektoren er gitt ved:
<math>|\vec{v_1} \times \vec{v_2}| = |\vec{v_1}| \cdot |\vec{v_2}|\cdot \sin \phi, \quad \phi \in [0^{\circ},180^{\circ}]</math>.
Bruksområder
Vektorproduktet brukes til å beskrive fenomener i fysikken og det kan også brukes til å regne ut arealer og volumer, samt til å bestemme et plans normalvektor. Eksempelvis har vi at:
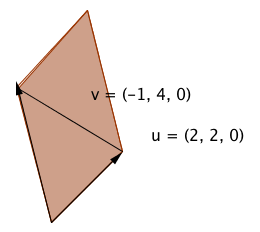
Arealet at parallellogram
utspent av vektorene <math>\vec{v_1}</math> og <math>\vec{v_2}</math> er gitt ved <math>A = |\vec{v_1} \times \vec{v_2}| </math>
Vektorene[-1, 4,0] og[2,2,0] ligger begge i xy planet og utspenner et parallellogram med areal 10, se figur til venstre. Ved å ta kryssproduktet får man vektoren [0, 0, 10] som jo er parallel med Z aksen, normalt på de to vektorene i xy planet. Denne vektoren har lengde 10, som jo er sammenfallende med arealet av parallellogrammet.
Arealet av en trekant
utspent av vektorene <math>\vec{v_1}</math> og <math>\vec{v_2}</math> er gitt ved <math>A = \frac 12\cdot|\vec{v_1} \times \vec{v_2}| </math>
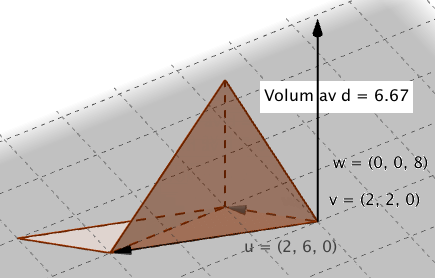
Volumet av en trekantet pyramide
bestemt av vektorene <math>\vec{v_1}</math>, <math>\vec{v_2}</math> og <math>\vec{v_3}</math> er gitt ved <math>V= \frac 16 \cdot|(\vec{v_1}\times \vec{v_2})\cdot \vec{v_3}|</math>
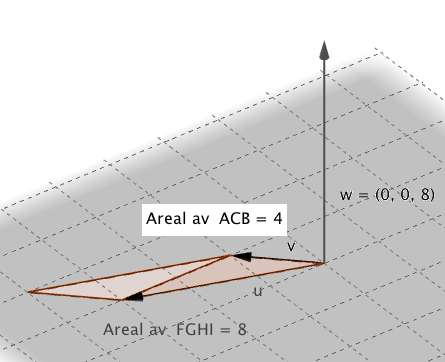
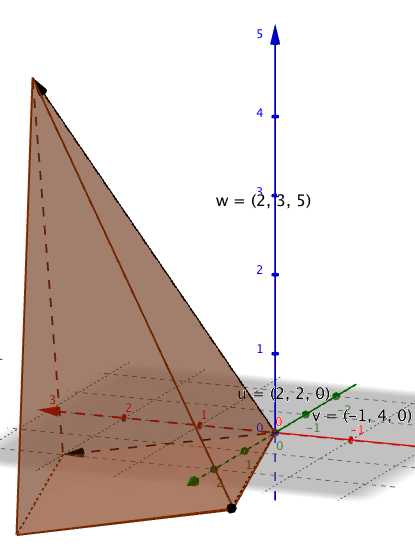
Volumet av en firkantet pyramide
bestemt av vektorene <math>\vec{v_1}</math>, <math>\vec{v_2}</math> og <math>\vec{v_3}</math> er gitt ved <math>V= \frac 13 \cdot |(\vec{v_1} \times \vec{ v_2})\cdot \vec{v_3}|</math>
Volumet av et parallellepiped
bestemt av vektorene <math>\vec{v_1}</math>, <math>\vec{v_2}</math> og <math>\vec{v_3}</math> er gitt ved <math>V = |(\vec{v_1}\times \vec {v_2})\cdot \vec{v_3}|</math>