Bokstavregning: Forskjell mellom sideversjoner
| (50 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
Algebra, eller bokstavregning, viser generelle sammenhenger. Tallregning eller aritmetikk gir oss mer spesielle sammenhenger. | Algebra, eller bokstavregning, viser generelle sammenhenger. Tallregning eller aritmetikk gir oss mer spesielle sammenhenger. | ||
| Linje 9: | Linje 8: | ||
En sirkel har radius 10 cm. Hva er arealet av sirkelen? | En sirkel har radius 10 cm. Hva er arealet av sirkelen? | ||
Arealet blir: < | Arealet blir: <math>A= 10cm \cdot 10cm \cdot \pi = 314,2 cm^2</math>. Men, det gjelder bare når radius i sirkelen er 10 cm. For alle andre radier er dette arealet feil. | ||
Et areal som gjelder for alle radier er: < | Et areal som gjelder for alle radier er: <math> A= \pi r^2</math> | ||
Bokstaver gir en formel som er allmenngyldig mens aritmetikken (tallregning)fokuserer på en eller flere spesielle tallverdier. | Bokstaver gir en formel som er allmenngyldig mens aritmetikken (tallregning) fokuserer på en eller flere spesielle tallverdier. | ||
== Regneregler == | == Regneregler == | ||
| Linje 23: | Linje 22: | ||
Når man regner med tall og parenteser har man muligheten til å trekke sammen parentesene før man løser de opp, i algebra er denne muligheten begrenset da man ikke uten videre kan trekke sammen for eksempel a + b. | Når man regner med tall og parenteser har man muligheten til å trekke sammen parentesene før man løser de opp, i algebra er denne muligheten begrenset da man ikke uten videre kan trekke sammen for eksempel a + b. | ||
< | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
'''Regel:'''<p></p> | '''Regel:'''<p></p> | ||
a + b = b + a<p></p> | a + b = b + a<p></p> | ||
</ | </div> | ||
< | |||
'''Eksempel:'''<p></p> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel 1:'''<p></p> | |||
4 + 2 = 2 + 4 = 6<p></p> | 4 + 2 = 2 + 4 = 6<p></p> | ||
</ | </div> | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
'''Regel:'''<p></p> | '''Regel:'''<p></p> | ||
(a + b) + c = a + (b + c) <p></p> | (a + b) + c = a + (b + c) <p></p> | ||
</ | </div> | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:'''<p></p> | '''Eksempel 2:'''<p></p> | ||
(a+5)+a = a +(5+a) = 2a+5<p></p> | (a+5)+a = a +(5+a) = 2a+5<p></p> | ||
</ | </div> | ||
< | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
'''Regel:'''<p></p> | '''Regel:'''<p></p> | ||
a + a + a + a = 4a <p></p> | a + a + a + a = 4a <p></p> | ||
</ | </div> | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:'''<p></p> | '''Eksempel 3:'''<p></p> | ||
a + b + 4 + 3a - 2 -b = 4a - 2<p></p> | a + b + 4 + 3a - 2 -b = 4a - 2<p></p> | ||
</ | </div> | ||
< | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
'''Regel:'''<p></p> | '''Regel:'''<p></p> | ||
< | <math> a \cdot a \cdot a = a^3</math> <p></p> | ||
</ | </div> | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 4:'''<p></p> | |||
<math> 3 \cdot x \cdot 2 \cdot y \cdot x \cdot y \cdot y = 3 \cdot 2 \cdot x \cdot x \cdot y \cdot y \cdot y = 6x^2y^3</math><p></p> | |||
</div> | |||
< | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
'''Regel:'''<p></p> | '''Regel:'''<p></p> | ||
< | <math> a \cdot b = b \cdot a </math><p></p> | ||
</ | </div> | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 5:'''<p></p> | |||
<math>y \cdot x \cdot 3 \cdot y = 3xy^2</math><p></p> | |||
</div> | |||
< | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
'''Regel:'''<p></p> | '''Regel:'''<p></p> | ||
(a+b)(c+d) = ac + ad + bc + bd <p></p> | (a+b)(c+d) = ac + ad + bc + bd <p></p> | ||
</ | </div> | ||
< | |||
'''Eksempel:'''<p></p> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
< | '''Eksempel 6:'''<p></p> | ||
</ | <math>(5+2x)(x+3y) = 5x+15y+2x^2+6xy</math><p></p> | ||
</div> | |||
< | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
'''Regel:'''<p></p> | '''Regel:'''<p></p> | ||
a(b + c) = ab + ac <p></p> | a(b + c) = ab + ac <p></p> | ||
</ | </div> | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:'''<p></p> | '''Eksempel 7:'''<p></p> | ||
3(2x +y) = 6x+3y <p></p> | 3(2x +y) = 6x+3y <p></p> | ||
</ | </div> | ||
Test deg selv | [http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=B22%2BB23%2BB24%2BB25%2BB26%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | ||
== Første kvadratsetning == | == Første kvadratsetning == | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
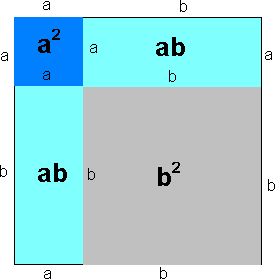
<math>(a +b)^2 = a^2 + 2ab + b^2</math> | |||
<p></p> Grafisk kan formelene over se slik ut: | <p></p> Grafisk kan formelene over se slik ut: | ||
<p></p> | <p></p> | ||
[[Bilde:Forste.png]]<p></p> | [[Bilde:Forste.png]]<p></p> | ||
</ | </div> | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel'''<p></p> | '''Eksempel 8:'''<p></p> | ||
Regn ut: | Regn ut: | ||
< | <math> (x+2)^2 </math><p></p> | ||
Man får:<p></p> < | Man får:<p></p> <math>(x + 2)^2 = x^2 + 4x + 4</math> | ||
<p></p> | <p></p> | ||
</ | </div> | ||
<p></p> | <p></p> | ||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A53%2BA54%2BA55%2BA56%2BA57%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | [http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A53%2BA54%2BA55%2BA56%2BA57%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | ||
< | |||
'''Eksempel'''<p></p> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
Faktoriser < | '''Eksempel 9:'''<p></p> | ||
Man får:<p></p> < | Faktoriser <math>9 + 12x + 4x^2</math><p></p> | ||
Man får:<p></p> <math> 9 + 12x + 4x^2 = (3 + 2x)^2 </math> | |||
<p></p> | <p></p> | ||
</ | </div> | ||
For å kjenne igjen kvadratsetningene denne veien må man ha øvd en del samtidig som man alltid må ha dem i bakhodet når det er snakk om faktorisering.<p></p> | For å kjenne igjen kvadratsetningene denne veien må man ha øvd en del samtidig som man alltid må ha dem i bakhodet når det er snakk om faktorisering.<p></p> | ||
| Linje 132: | Linje 148: | ||
== Andre kvadratsetning == | == Andre kvadratsetning == | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
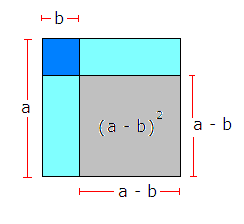
< | <math>(a - b)^2 = a^2 - 2ab + b^2 </math> | ||
<p></p> | <p></p> | ||
[[Bilde:Andre.png]]<p></p></ | [[Bilde:Andre.png]]<p></p></div> | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 10:''' <p></p> | |||
Regn ut<p></p> <math>(x - 2y)^2</math> | |||
<p></p> | |||
Løsning<p></p> | |||
<math>x^2- 4xy + 4y^2 </math> | |||
<p></p></ | <p></p></div> | ||
<p></p> | <p></p> | ||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A5D%2BA5E%2BA5F%2BA60%2BA61%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 11:'''<p></p> | |||
Faktoriser <math>x^2-12x+36</math><p></p> | |||
Løsning:<p></p> | |||
<math>(x-6)^2 </math> | |||
<p></p></div> | |||
<p></p> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A62%2BA63%2BA64%2BA65%2BA66%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
== Konjugatsetningen (3. Kvadratsetning) == | == Konjugatsetningen (3. Kvadratsetning) == | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
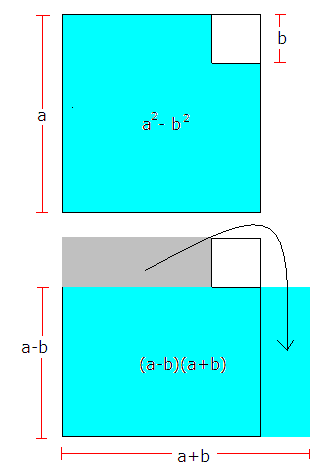
< | <math>a^2 - b^2 = (a+b)(a-b)</math> | ||
<p></p> Grafisk kan likningen tolkes slik: | <p></p> Grafisk kan likningen tolkes slik: | ||
<p></p> | <p></p> | ||
[[Bilde:Tredje.png]]<p></p> | [[Bilde:Tredje.png]]<p></p> | ||
</ | </div> | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
<p></p> | |||
< | '''Eksempel 12:''' <p></p> | ||
Regn ut < | Regn ut <math>(x- 4)(x+4)</math><p></p> | ||
< | Løsning<p></p> | ||
<math>x^2-16 </math> | |||
<p></p></ | <p></p></div> | ||
<p></p> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A67%2BA68%2BA69%2BA6A%2BA6B%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
<p></p>'''Eksempel 13:''' <p></p> | |||
Eksempel 13: | Faktoriser<p></p><math>x^2-1</math><p></p>Løsning<p></p> | ||
Faktoriser | <math>(x-1)(x+1) </math> | ||
Her må man huske at <math>1^2 = 1 </math> | |||
<p></p></div> | |||
<p></p> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A6C%2BA6D%2BA6E%2BA6F%2BA70%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
Her | |||
== Forkorting == | == Forkorting == | ||
| Linje 208: | Linje 228: | ||
Fra tallregningen er vi vant med at svaret blir et tall bestående av et eller flere siffer. Når man driver med bokstavregning blir svaret gjerne en blanding av tall, bokstaver og brøk. | Fra tallregningen er vi vant med at svaret blir et tall bestående av et eller flere siffer. Når man driver med bokstavregning blir svaret gjerne en blanding av tall, bokstaver og brøk. | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
<p></p>'''Eksempel 14:''' <p></p> | |||
Skriv<math> \frac{x^2-1}{x+1} </math> enklest mulig.<p></p>Løsning<p></p> | |||
<math> \frac{x^2-1}{x+1} = \frac{(x-1)(x+1)}{x+1} = x-1</math> | |||
<p></p></div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
<p></p>'''Eksempel 15:''' <p></p> | |||
Skriv<math> \frac{x-1}{x^2-1} </math> enklest mulig.<p></p>Løsning<p></p> | |||
<math> \frac{x-1}{x^2-1} = \frac{x-1}{(x-1)(x+1)} = \frac {1}{x+1}</math> | |||
<p></p></div> | |||
Test deg selv | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
<p></p>'''Eksempel 16:''' <p></p> | |||
Skriv <math> \frac{(x+3)^2}{x^2 +6x +9} </math> enklest mulig.<p></p>Løsning<p></p> | |||
<math> \frac{(x+3)^2}{(x+3)(x+3)} = \frac{(x+3)(x+3)}{(x+3)(x+3)} = 1</math> | |||
<p></p></div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
<p></p>'''Eksempel 17''' <p></p> | |||
Skriv enklest mulig:<p></p><math> \frac{x^2 - 6x + 9}{2x^2-18}</math><p></p> | |||
Løsning:<p></p> | |||
<math> \frac{x^2 - 6x + 9}{2x^2-18} = \\ \frac{(x-3)(x-3)}{2(x^2-9)}\\ \frac{(x-3)(x-3)}{2(x-3)(x+3)} = \\ \frac{(x-3)}{2(x+3)}</math> | |||
<p></p></div> | |||
---- | |||
[[Ungdomstrinn Hovedside | Tilbake til Ungdomstrinn Hovedside]]<p></p> | |||
[[Hovedside| Tilbake til hovedside]] | |||
[[Category:Algebra]] | |||
[[Category:U - trinn]] [[Category:Ped]] | |||
Siste sideversjon per 2. feb. 2017 kl. 20:52
Algebra, eller bokstavregning, viser generelle sammenhenger. Tallregning eller aritmetikk gir oss mer spesielle sammenhenger.
Hvorfor bokstaver?
En sirkel har radius 10 cm. Hva er arealet av sirkelen?
Arealet blir: <math>A= 10cm \cdot 10cm \cdot \pi = 314,2 cm^2</math>. Men, det gjelder bare når radius i sirkelen er 10 cm. For alle andre radier er dette arealet feil.
Et areal som gjelder for alle radier er: <math> A= \pi r^2</math>
Bokstaver gir en formel som er allmenngyldig mens aritmetikken (tallregning) fokuserer på en eller flere spesielle tallverdier.
Regneregler
Se på uttrykket 2x + 4ab
- LEDD, utrykket består av to ledd, 2x og 4ab. Ledd adskilles med pluss eller minus.
- FAKTOR, leddet 2x er et PRODUKT av to faktorer; 2 og x. Faktorer adskilles med multiplikasjonstegn (gangetegn). Dersom det ikke kan missforståes er det vanlig å utelate multiplikasjonstegnet. 4ab er et produkt av faktorene 4, a og b. Man kunne ha skrevet 4ab som 4∙a∙b, men siden det ikke er grunnlag for å misforstå sløyfer vi gangetegnet.
Når man regner med tall og parenteser har man muligheten til å trekke sammen parentesene før man løser de opp, i algebra er denne muligheten begrenset da man ikke uten videre kan trekke sammen for eksempel a + b.
Første kvadratsetning
Regn ut:
<math> (x+2)^2 </math> Man får: <math>(x + 2)^2 = x^2 + 4x + 4</math>
For å kjenne igjen kvadratsetningene denne veien må man ha øvd en del samtidig som man alltid må ha dem i bakhodet når det er snakk om faktorisering.
Andre kvadratsetning
<math>x^2- 4xy + 4y^2 </math>
<math>(x-6)^2 </math>
Konjugatsetningen (3. Kvadratsetning)
<math>x^2-16 </math>
<math>(x-1)(x+1) </math> Her må man huske at <math>1^2 = 1 </math>
Forkorting
Poenget med å forkorte et uttrykk er ønsket om å skrive det enklest mulig. Dersom et brøk uttrykk har en fator med samme verdi både i teller og nevner kan disse forkortes. Før man forkorter må man faktorisere. Det er ikke alle uttrykk som lar seg forkorte.
Fra tallregningen er vi vant med at svaret blir et tall bestående av et eller flere siffer. Når man driver med bokstavregning blir svaret gjerne en blanding av tall, bokstaver og brøk.
<math> \frac{x^2-1}{x+1} = \frac{(x-1)(x+1)}{x+1} = x-1</math>
<math> \frac{x-1}{x^2-1} = \frac{x-1}{(x-1)(x+1)} = \frac {1}{x+1}</math>
Test deg selv
<math> \frac{(x+3)^2}{(x+3)(x+3)} = \frac{(x+3)(x+3)}{(x+3)(x+3)} = 1</math>
<math> \frac{x^2 - 6x + 9}{2x^2-18} = \\ \frac{(x-3)(x-3)}{2(x^2-9)}\\ \frac{(x-3)(x-3)}{2(x-3)(x+3)} = \\ \frac{(x-3)}{2(x+3)}</math>