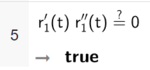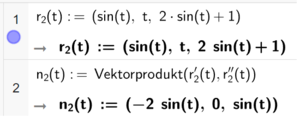R2 2023 høst LØSNING: Forskjell mellom sideversjoner
| Linje 294: | Linje 294: | ||
[[File: R2_H23_del2_5c.png|300px]] | [[File: R2_H23_del2_5c.png|300px]] | ||
Definerer normalvektoren til planet, og vektoren for y-aksen. Bruker CAS til å finne vinkelen mellom disse to vektorene, og får vite at vinkelen mellom normalvektoren og y-aksen er $\frac{\pi}{4}$. Normalvektoren til planet ligger 90 grader (altså $\frac{\pi}{2}$) på planet. Vinkelen mellom smygplanet og y-aksen er altså $\frac{\pi}{2}- \frac{\pi}{4}= \frac{\pi}{4}$. | Definerer normalvektoren til planet, og vektoren for y-aksen. Bruker CAS til å finne vinkelen mellom disse to vektorene, og får vite at vinkelen mellom normalvektoren og y-aksen er $\frac{\pi}{4}$. Normalvektoren til planet ligger 90 grader (altså $\frac{\pi}{2}$) på planet. Vinkelen mellom smygplanet og y-aksen er altså $\frac{\pi}{2}- \frac{\pi}{4}= \frac{\pi}{4}$. Vinkelen er altså konstant. | ||
===d)=== | ===d)=== | ||
Bruker CAS til å finne normalvektoren til den nye kurven. | |||
Hele kurven ligger i ett plan. | [[File: R2_H23_del2_5d.png|300px]] | ||
Smygplanets normalvektor har alltid 0 som y-koordinat. Det vil si at smygplanet alltid er parallellt med y-aksen (eller på y-aksen), for alle verdier av t. Hele kurven ligger i ett plan. | |||
Siste sideversjon per 22. jul. 2024 kl. 08:14
Løsningsforslag fra Lektor Seland
Videoløsning del 1 av Lektor Lainz
Videoløsning del 2 av Lektor Lainz
Løsningsforslag laget av OpenMathBooks prosjektet
DEL 1
Oppgave 1
$\int_{-1}^{1}(x^3+2x)dx$
$=[\frac 14 x^4+x^2]_{-1}^{1}$
$=(\frac 14+1)-(\frac 14+1)=0$
Svaret forteller meg enten at arealet av området som er avgrenset av grafen, x-aksen og linjene x = −1 og x = 1 er lik 0, eller at det er et like stort område over og under x-aksen i dette intervallet. Det er det siste som er tilfellet her.
Oppgave 2
Den blå grafen er g(x)=sin x, fordi sin(0)=0. Den rød grafen er da f(x)=cos x, og den krysser y-aksen i y=1 fordi cos(0)=1.
Skjæringspunkt mellom f og g:
$sin\, x = cos\, x$
$x = \frac{\pi}{4} +k\pi$
Skjæringspunktene mellom f og g i det fargelagte området:
$x=-\frac{3\pi}{4}$ og $x=\frac{\pi}{4}$
Areal av det fargelagte området:
$\int_{-\frac{3\pi}{4}}^{\frac{\pi}{4}} cos\,x\,dx - \int_{-\frac{3\pi}{4}}^{\frac{\pi}{4}} sin\,x\,dx$
$=(sin\,(\frac{\pi}{4}) - sin (-\frac{3\pi}{4})-(-cos\,(\frac{\pi}{4})+cos(-\frac{3\pi}{4}))$
$=\frac{\sqrt2}{2}-(-\frac{\sqrt2}{2})-(-\frac{\sqrt2}{2}+(-\frac{\sqrt2}{2}))$
$=2\frac{\sqrt2}{2}+2\frac{\sqrt2}{2}=4\frac{\sqrt2}{2}=2\sqrt2$
Arealet av det fargelagte området vist på figuren er $2\sqrt2$.
Oppgave 3
a)
$S = \frac{a_1}{1-k}$
Siden rekken konverger mot 8 må k være $\frac 12 $ :
$8 = \frac{4}{1-k} \Rightarrow k= \frac 12$
$S_4 = 4+2+1+ \frac 12 = 7,5$
b)
I en aritmetisk rekke øker leddene med en fast verdi d.
$a_1 = a_4 - 3d $
$a_7 = a_4 + 3d$
$a_1 + a_4 + a_7 = 114$
$a_4 -3d + a_4 + a_4 +3d =114$
$3 a_4 = 114$
$a_4 = 38$
Oppgave 4
a)
Vi har $\alpha: x-2y+2z+1=0$ og $A(4,2,2)$
$\vec{n}_{\alpha}=[1,-2,2]$
$l=\begin{cases} x = 4+t \\ y = 2-2t \\ z = 2+2t \end{cases}$
b)
$d=\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}$, der $(x_0,y_0,z_0)$ er koordinatene til punkt A.
$=\frac{1\cdot4-2\cdot2+2\cdot2+1}{\sqrt{1^2+(-2)^2+2^2}}$
$=\frac{5}{\sqrt9}=\frac53$
Asvtanden fra A til $\alpha$ er $\frac{5}{3}$
Oppgave 5
a)
Programmet regner ut arealet av flaten som er avgrenset av f(x), x- aksen, linjen x = -2 og linjen x = 2.
b)
$f(x) = x^2-1$
Funksjonen har nullpunkter for x=-1 og x= 1. Mellom disse ligger den under x aksen. Den er symmetrisk om y-aksen. Vi integrerer fra -2 til -1 og fra -1 til 0. Til slutt multipliserer vi med 2, for å finne hele arealet.
$A= 2 \cdot ( \int_{-2}^{-1}(x^2-1)dx +| \int_{-1}^{-0}(x^2-1))dx | $
$ = 2 \cdot ( [\frac 13 x^3- x ]_{-2}^{-1} + | [ \frac 13 x^3 - x]_{-1}^{0}) | $
$= 2 \cdot ( (\frac {-1}{3}+1) -( \frac {-8}{3} +2) + | ((0)- (\frac{-1}{3} + 1) |$
$ = 2 \cdot ( \frac 43 + \frac 23) $
$ = 2 \cdot \frac 63 $
$= 4$
Oppgave 6
Arealet av sideflaten BCGF er
$\frac12 |\vec{BF}\times\vec{BC}|+\frac12 |\vec{GF}\times\vec{GC}|$
Regner ut $\vec{BF}\times\vec{BC}$
$=\begin{vmatrix} \vec i & \vec j & \vec k\\ -1 & -1 & 3\\ -4 & 0 & 0 \end{vmatrix} $
$=0\vec i -12\vec j -4\vec k$
$=[0,-12,-4]$
Regner ut $\vec{GF}\times\vec{GC}$
$=\begin{vmatrix} \vec i & \vec j & \vec k\\ 2 & 0 & 0\\ -1 & 1 & -3 \end{vmatrix}$
$=0\vec i +6\vec j +2\vec k$
$=[0,6,2]$
Arealet av sideflaten BCGF er
$\frac12 |\vec{BF}\times\vec{BC}|+\frac12 |\vec{GF}\times\vec{GC}|$
$\frac12 |[0,-12,-4]|+\frac12 |[0,6,2]|$
$=\frac12 \sqrt{0^2+12^2+4^2}+\frac12\sqrt{0^2+6^2+2^2}$
$=\frac12 \sqrt{160}+\frac12\sqrt{40}$
$=\frac12 \cdot 4\sqrt{10}+\frac12\cdot2\sqrt{10}$
$=3\sqrt{10}$
DEL 2
Oppgave 1
a)
Bruker regresjonsanalyse i Geogebra og velger en sinusfunksjon som modell.
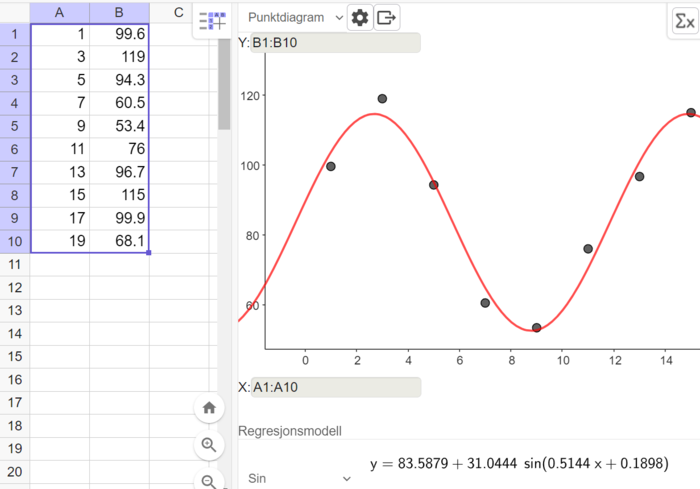
Modellen for vannstanden ved verftet er $f(x)=31sin(0,514x+0,19)+83,6$
b)
Bruker CAS i Geogebra. Den 25. april begynner 24 timer etter 24. april.
 Ifølge modellen vil vannstanden øke raskest ca. 24,1t og 36,3t etter 24. april, altså like etter midnatt og like etter kl. 12 den 25. april.
Ifølge modellen vil vannstanden øke raskest ca. 24,1t og 36,3t etter 24. april, altså like etter midnatt og like etter kl. 12 den 25. april.
c)
Løser oppgaven grafisk i Geogebra denne gangen.
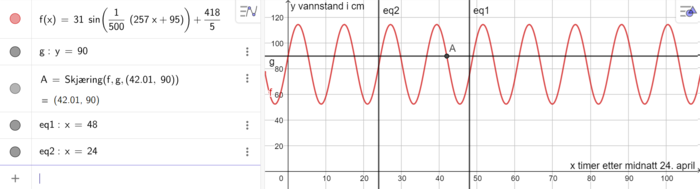
De kan senest starte med å slepe ut plattformen 42 - 2 = 40 timer etter 24. april, altså kl. 16 den 25. april.
Oppgave 2
a)
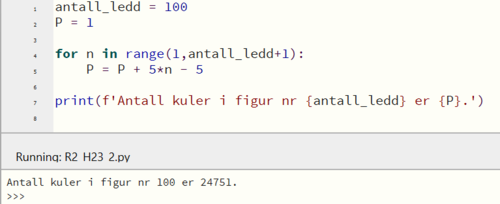
$P_1=1$
Etter det øker antall kuler i figuren med 5*(n-1) for hver figur.
$P_2=P_1+5\cdot1$
$P_3=P_2+5\cdot2$
$P_n=P_{n-1}+5\cdot(n-1) = P_{n-1}+5n-5$
b)
Programmerer i Python.
$P_{100}=24\,751$
c)
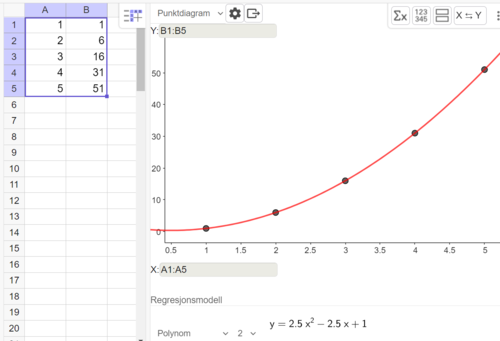
Bruker regresjonsanalyse i Geogebra for å finne en eksplisitt formel.
$P_n=2,5n^2-2,5n+1$
Vi skal vise at $P_{n-1}+5n-5=2,5n^2-2,5n+1$. Bruker CAS i Geogebra.
Vi sjekker først om formelen stemmer for n=1 (se linje 2 i CAS). Formelen stemmer for n=1, siden $P_1=1$.
Vi antar nå at formelen stemmer for n = k, og sjekker om formelen stemmer for n = k + 1. Da vil $P_{k+1}=P_k+5(5+1)-5$. Se linje 3 og 4 i CAS.
Vi har nå vist at dersom formelen stemmer for n=k , må den også stemme for n=k+1. Siden formelen stemmer for n=1, stemmer den for n=2, osv. $P_k\Rightarrow P_{k+1}$.
Oppgave 3
Bruker CAS i Geogebra.
Volumet av tønnen er omtrent 145 562 kubikkcentimeter, det vil si ca. 145,6 L.
Oppgave 4
a)
Vi har $M(t)=A\cdot sin(ct+k)+d$
Perioden er på 24 timer.
$\frac{2\pi}{c}=24$
$c = \frac{\pi}{12}$
Amplituden A:
$A=\frac{31,2-18,2}{2}=\frac{13}{2}=6,5$
Likevektslinja d:
$d=18,2+\frac{13}{2}=\frac{247}{10}=24,7$
b)
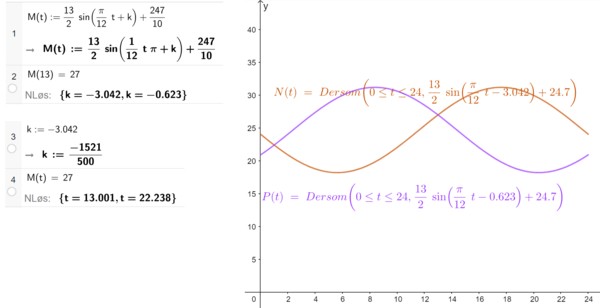
Bruker Geogebra.
Jeg bruker opplysningen om at $M(13)=27$ for å finne k (se linje 2 i CAS). Deretter tegner jeg en grafene N og P, med hver sin k-verdi fra linje 2. Jeg ser at den oransje grafen til N stemmer med at forurensningen øker på morgenen (fra ca. kl. 6) og avtar på kvelden (fra ca. kl. 18). Det vil si at k=-3.042. Jeg angir dette i CAS (linje 3), og løser $M(t)=27$. Da får jeg tidspunktene $t=13$ og $t=22.24$
Det andre tidspunktet luftforurensningen er på $27\,\mu g/m^3$ er ca. kl. 22:14.
Oppgave 5
a)
p er normalvektoren til xy-planet. Skalarproduktet av p og den deriverte av $r_1(t)$ er lik 0 der hvor den deriverte er parallell med xy-planet (står da ortogonalt på p).
Tangenten i punktet $(0,\pi,-1)$ er parallell med xy-planet.
b)
Bruker CAS til å sjekke om skalarproduktet mellom $r_1'(t)$ og $r_1"(t)$ alltid er 0.
Siden dette er "True" (sant) gjelder det for alle t.
c)
Bruker CAS i Geogebra.
Definerer normalvektoren til planet, og vektoren for y-aksen. Bruker CAS til å finne vinkelen mellom disse to vektorene, og får vite at vinkelen mellom normalvektoren og y-aksen er $\frac{\pi}{4}$. Normalvektoren til planet ligger 90 grader (altså $\frac{\pi}{2}$) på planet. Vinkelen mellom smygplanet og y-aksen er altså $\frac{\pi}{2}- \frac{\pi}{4}= \frac{\pi}{4}$. Vinkelen er altså konstant.
d)
Bruker CAS til å finne normalvektoren til den nye kurven.
Smygplanets normalvektor har alltid 0 som y-koordinat. Det vil si at smygplanet alltid er parallellt med y-aksen (eller på y-aksen), for alle verdier av t. Hele kurven ligger i ett plan.