2PY 2024 vår LØSNING LK20: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| (30 mellomliggende versjoner av en annen bruker er ikke vist) | |||
| Linje 4: | Linje 4: | ||
[https://lektorodd.github.io/lf/2PY-V24/ Løysing laga av Torodd F. Ottestad] | [https://lektorodd.github.io/lf/2PY-V24/ Løysing laga av Torodd F. Ottestad] | ||
[https://kublakanutdanning.no/eksamen-2p-y-varen-2024/ Videoløsning av KublaKan Utdanning] | |||
=DEL 1= | =DEL 1= | ||
==Oppgave 1== | |||
Sjekker om k = y/x er den samme for alle prisene som er oppgitt. | |||
$\frac{25}{2}=12,5$ kroner per sjokolade | |||
$\frac{100}{8}=12,5$ kroner per sjokolade | |||
$\frac{200}{16}=\frac{100}{8}=12,5$ kroner per sjokolade | |||
$\frac{300}{24}=\frac{100}{8}=12,5$ kroner per sjokolade | |||
Prisen per sjokolade er den samme uansett, så den <b>totale</b> prisen er proporsjonal med antall sjokolader du kjøper. | |||
Antall sjokolader du kjøper, og prisen du betaler <i>for hver sjokolade</i>, er ikke proporsjonale. Det er ikke godt å si hva oppgaveforfatteren mente her. | |||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 18: | Linje 36: | ||
Det blir 25 % billigere per bagett å kjøpe fire bagetter, enn å kjøpe to bagetter. | Det blir 25 % billigere per bagett å kjøpe fire bagetter, enn å kjøpe to bagetter. | ||
==Oppgave 3== | |||
$700\,000\cdot 150\cdot 30=3\,150\,000\,000=3,15\cdot 10^9$ | |||
Dette blir ca. $3,15\cdot 10^9$ liter vann i løpet av én måned. Jeg har her antatt at én måned har 30 døgn. | |||
==Oppgave 4== | |||
<table> | |||
<tr> | |||
<th>Figur nr </th> | |||
<th>Formel</th> | |||
<th>Antall sirkler</th> | |||
</tr> | |||
<tr> | |||
<td>$1$</td> | |||
<td>$2\cdot (2\cdot 2) -1$</td> | |||
<td>$7$</td> | |||
</tr> | |||
<tr> | |||
<td>$2$</td> | |||
<td>$2\cdot (3\cdot 3) -1$</td> | |||
<td>$17$</td> | |||
</tr> | |||
<tr> | |||
<td>$3$</td> | |||
<td>$2\cdot (4\cdot 4)-1$</td> | |||
<td>$31$</td> | |||
</tr> | |||
<tr> | |||
<td>$4$</td> | |||
<td>$2\cdot(5\cdot 5)-1$</td> | |||
<td>$29$</td> | |||
</tr> | |||
<tr> | |||
<td>$9$</td> | |||
<td>$2\cdot(10\cdot 10)-1$</td> | |||
<td>$199$</td> | |||
</tr> | |||
<tr> | |||
<td>$n$</td> | |||
<td>$2\cdot (n+1)^2-1= 2\cdot (n^2+2n+1)-1=2n^2+4n+1$</td> | |||
<td></td> | |||
</tr> | |||
</table> | |||
===a)=== | |||
Det vil være 29 sirkler i figur 4 og 199 sirkler i figur 9. | |||
===b)=== | |||
Mønsteret er slik det er vist i tabellen øverst i svaret. Antall sirkler i figur n er $2n^2+4n+1$. | |||
=DEL 2= | |||
==Oppgave 1== | |||
===a)=== | |||
Hytta koster 18 000 kroner å leie, og det kan være fra 1 til 12 personer på hytta. | |||
===b)=== | |||
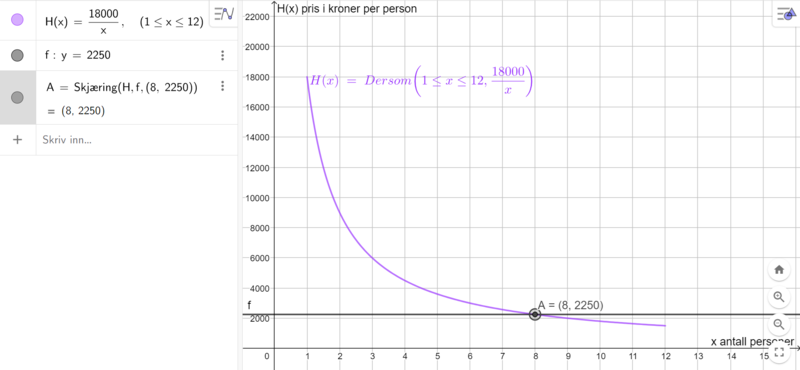
[[File: 2P-Y_V24_del2_1b.png|800px]] | |||
Skjæringspunktet mellom grafen til H og den rette linjen y=2250 er (8,2250). Det betyr at dersom 8 venner leier hytta sammen, må hver av dem betale 2250 kroner hver. | |||
===c)=== | |||
[[File: 2P-Y_V24_del2_1c.png|800px]] | |||
Stigningstallet til den rette linjen som går gjennom punktene (6,H(6)) og (12,H(12)) er -250. Det betyr at fra 6 til 12 personer som leier hytta sammen, går prisen per person gjennomsnittlig ned med 250 kroner per ekstra person som er med på å dele leien. | |||
==Oppgave 2== | |||
===a)=== | |||
$5,4 - 5,15 = 0,25$ | |||
Renten er 0,25 prosentpoeng høyere dersom hun velger 1 år i stedet for 3 måneder. | |||
$\frac{0,25}{5,15}\cdot 100=4,85$ | |||
Renten er 4,85 % høyere dersom hun velger 1 år i stedet for 3 måneder. | |||
===b)=== | |||
$450\,000\cdot\frac{5,4}{100}=24300$ | |||
Malin får 24 300 kroner i renteinntekter dersom hun velger å binde pengene i 1 år. | |||
==Oppgave 3== | |||
===a)=== | |||
Bruker Geogebra til å finne statistikk for Solveigs skiturer: | |||
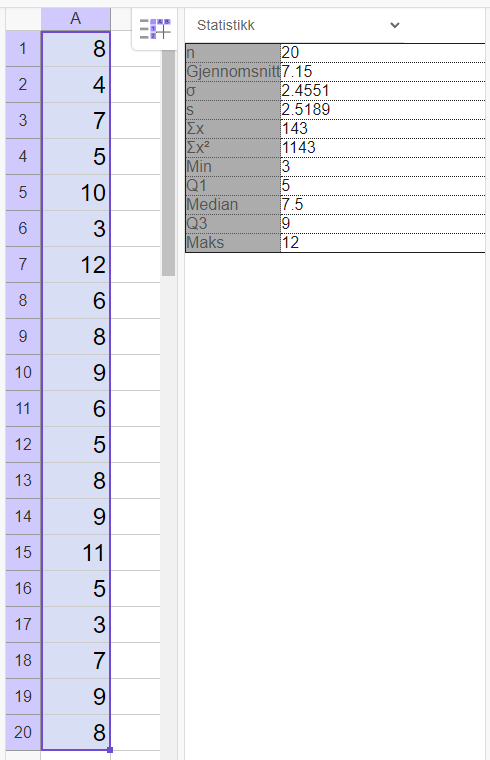
[[File: 2P_V24_del2_2a.png]] | |||
I gjennomsnitt brukte Solveig 7,15 timer per skitur, mens Miriam brukte 4,7 timer per skitur. Gjennomsnittlig varte altså skiturene til Solveig lengre. | |||
Medianen for Solveigs skiturer var 7,5 timer, mot 4 timer for Miriam. Det vil si at halvparten av skiturene til Solveig varte mer enn 7,5 timer, mens halvparten av skiturene til Miriam varte mer enn 4 timer. | |||
Standardavviket for Solveigs skiturer er ca. 2,5 timer, med for Miriam er det 4,2. Det vil si at Miriam har større variasjon i varigheten på skiturene. Hun kan ha hatt noen veldig korte og noen veldig lange skiturer. Solveig holder seg nærmere gjennomsnittsvarigheten på sine skiturer. | |||
Miriam har et gjennomsnitt som er høyere enn medianen, som vil si at hun har en eller flere lange skiturer som "drar opp" gjennomsnittet. | |||
Solveig har et gjennomsnitt som er lavere enn medianen, som vil si at hun har en eller flere korte skiturer som "drar ned" gjennomsnittet. | |||
===b)=== | |||
1) I den andre raden i tabellen står det at jentene gikk 11 skiturer på 3 timer eller mindre. I den tredje raden i tabellen står det at jentene gikk 14 skiturer på 5 timer eller mindre. Det må bety at 3 av skiturene var på 5 timer. | |||
2) Vi ser av tallene over oppgave a) at Solveig gikk fire skiturer på 8 timer. Tabellen i oppgave b) viser at jentene bare gikk tre skiturer på 8 timer sammen. Det vil si at Miriam ikke var med på én av 8-timers turene til Solveig. | |||
==Oppgave 4== | |||
===a)=== | |||
Tuva kan ha brukt eksponentiell regresjonsanalyse, som vist under i Geogebra. | |||
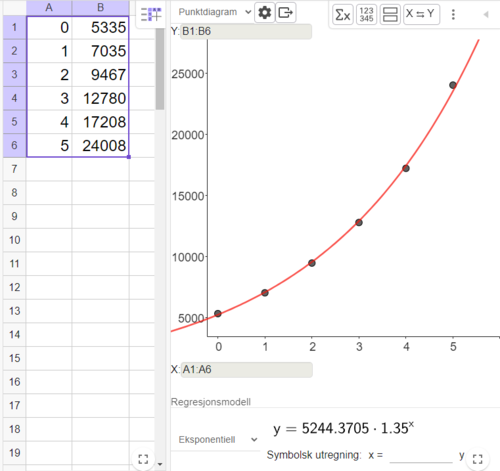
[[File: 2P_V24_del2_1a.png | 500 px]] | |||
I modellen $f(x)=5244\cdot1,35^x$ vekstfaktoren 1,35, som betyr en månedlig vekst på 35 % følgere. | |||
===b)=== | |||
Jeg forstår spørsmålet som at antall følgere skal øke med 40 % fra april til mai, og med 45 % fra mai til juni. | |||
Antall følgere i mai: $24008\cdot 1,40 \approx 33611$ | |||
Antall følgere i juni: $33611\cdot 1,45 \approx 48736$ | |||
===c)=== | |||
Jeg løser oppgaven i Excel. | |||
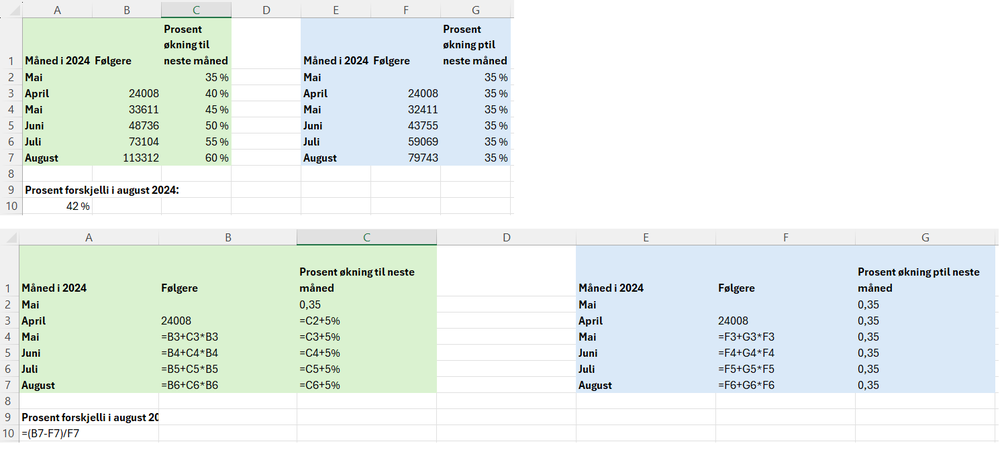
[[File: 2P_V24_del2_1c.png | 1000 px]] | |||
Tuva vil ha 42 % prosent flere følgere i august 2024 dersom hun klarer å nå det nye målet sitt for hver måned, sammenliknet med om økningen fortsetter å være på 35 % hver måned. | |||
==Oppgave 5== | |||
<b>Påstand 1</b>: "80 elever brukte mindre enn 40 minutter på lekser denne ettermiddagen." | |||
Vi ser på første søyle i histogrammet, og ganger klassebredden med høyden på søylen: $40 \cdot 2 = 80$. Dette gir oss en frekvens på 80 stykker i klassen 0-40 minutter med lekser. Påstanden er riktig. | |||
<b>Påstand 2</b>: "Den relative frekvensen for 100–150 minutter brukt på lekser er 1/5." | |||
Vi finner frekvensen for alle søylene til sammen: $40\cdot 2 + 20\cdot 6 + 40\cdot 5 + 50\cdot 2 = 80+120+200+100 = 500$ | |||
Frekvensen for klassen 100-150 minutter er 100. | |||
Den relative frekvensen for klassen 100-150 minutter er da 100 / 500 = 1/5. Påstanden er riktig. | |||
<b>Påstand 3</b>: "Elevene som brukte mindre enn 60 minutter på leksene, brukte i gjennomsnitt 38 minutter." | |||
80 elever brukte 0-40 minutter (gjennomsnittlig 20 minutter) og 120 elever brukte 40-60 minutter (gjennomsnittlig 50 minutter) på lekser. | |||
$\frac{80\cdot 20 + 120\cdot 50}{200} = \frac{7600\, min}{200\, elever}=38 \, min/elev$. Påstanden er riktig. | |||
<b>Påstand 4</b>: "For elevene som brukte mindre enn 60 minutter på leksene, er medianen for antall minutter høyere enn gjennomsnittet for antall minutter." | |||
80 elever brukte 0-40 minutter og 120 elever brukte 40-60 minutter på lekser. Det er 200 elever til sammen i disse to klassene, og det betyr at medianelevene nr. 100 og 101 er i klassen 40-60 minutter. Medianen er altså mer enn gjennomsnittet (38 minutter). Påstanden er riktig. | |||
==Oppgave 6== | |||
Linje 1: variabelen "innskudd" settes lik 27 500 (kroner). Det er hvor mye Thea kan sette inn på BSU-kontoen hvert år. | |||
Linje 2: variabelen "prosent_rente" settes lik 6,8 (%). Det er renten på BSU-kontoen. | |||
Linje 3: variabelen "BSU" settes lik 0. Det er hvor mye hun har på BSU-kontoen. Før hun begynner sparingen, er det 0 kroner. | |||
Linje 5: en for-løkka skal gå fra og med 2024 til (men ikke med) 2034. All koden linje 7-13 gjentas altså 10 ganger, som tilsvarer 10 år med sparing. | |||
Linje 7: beløpet på BSU-kontoen oppdateres med nytt innskudd. | |||
Linje 9: årets renter beregnes. | |||
Linje 11: beløpet på BSU-kontoen oppdateres med årets renter. | |||
Linje 13: året, årets renter og beløpet på BSU-kontoen skrives ut. | |||
Totalt sett vil programmet skrive ut året, årets renter, og beløpet på BSU-kontoen for hvert år fra 2024 til og med 2033. Jeg antar at Thea vil finne ut hvor mye hun har på BSU-kontoen etter 10 år med årlig sparing. | |||
==Oppgave 7== | |||
Bruker Excel til å lage diagrammer. | |||
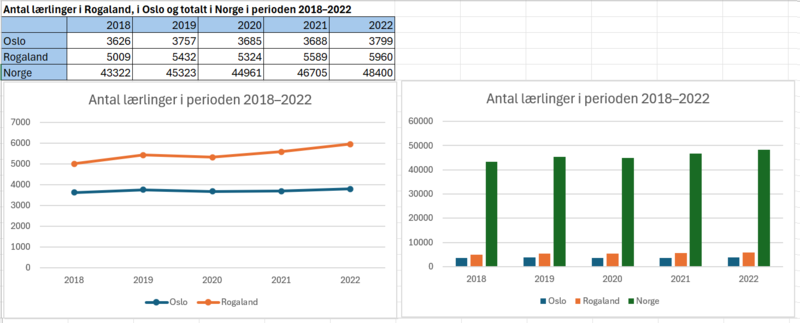
[[File: 2P-Y_V24_del2_8_1.png|800px]] | |||
Til venstre i bildet et linjediagram over utviklingen av antall lærlinger i Oslo og Rogaland fra 2018 til 2022. | |||
Til høyre i bildet et stolpediagram over antall lærlinger i Oslo, Rogaland og hele Norge fra 2018 til 2022. | |||
Antall lærlinger i Oslo har økt med $\frac{3779-3626}{3626}\cdot 100=4,8$ % fra 2018 til 2022. | |||
Antall lærlinger i Rogaland har økt med $\frac{5960-5009}{5009}\cdot 100=19$ % fra 2018 til 2022. Det er en mye større økning enn i Oslo! | |||
Antall lærlinger i Norge har økt med $\frac{48400-43322}{43322}\cdot 100=11,7$ % fra 2018 til 2022. Det vil si at antall lærlinger i Oslo har økt mindre enn landsgjennomsnittet, mens antall lærlinger i Rogaland har økt mer enn landsgjennomsnittet. | |||
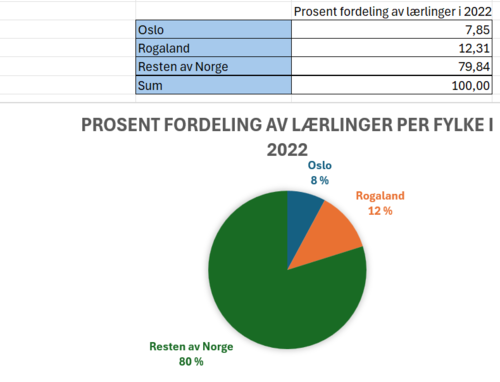
I 2022 utgjorde antall lærlinger i Oslo $\frac{3799}{48400}\cdot 100 = 7,9$ % av Norges lærlinger. | |||
I 2022 utgjorde antall lærlinger i Rogaland $\frac{5960}{48400}\cdot 100 = 12,3$ % av Norges lærlinger. | |||
[[File: 2P-Y_V24_del2_8_3.png|500px]] | |||
Her er det bare fantasien og tiden som setter grenser for hvor mange diagrammer og beregninger man kan gjøre... | |||
Siste sideversjon per 26. nov. 2024 kl. 08:37
Diskusjon av oppgaven på matteprat
Løysing laga av Torodd F. Ottestad
Videoløsning av KublaKan Utdanning
DEL 1
Oppgave 1
Sjekker om k = y/x er den samme for alle prisene som er oppgitt.
$\frac{25}{2}=12,5$ kroner per sjokolade
$\frac{100}{8}=12,5$ kroner per sjokolade
$\frac{200}{16}=\frac{100}{8}=12,5$ kroner per sjokolade
$\frac{300}{24}=\frac{100}{8}=12,5$ kroner per sjokolade
Prisen per sjokolade er den samme uansett, så den totale prisen er proporsjonal med antall sjokolader du kjøper.
Antall sjokolader du kjøper, og prisen du betaler for hver sjokolade, er ikke proporsjonale. Det er ikke godt å si hva oppgaveforfatteren mente her.
Oppgave 2
Pris per bagett i det første tilbudet: 32 kr / 2 = 16 kr
Pris per bagett i det andre tilbudet: 48 kr / 4 = 12 kr
Prisforskjell per bagett: 16 kr - 12 kr = 4 kr
Prosent forskjell i pris per bagett, sammenlignet med den dyreste prisen: $\frac{4}{16}\cdot 100\%=\frac{1}{4}\cdot 100\%=25\%$
Det blir 25 % billigere per bagett å kjøpe fire bagetter, enn å kjøpe to bagetter.
Oppgave 3
$700\,000\cdot 150\cdot 30=3\,150\,000\,000=3,15\cdot 10^9$
Dette blir ca. $3,15\cdot 10^9$ liter vann i løpet av én måned. Jeg har her antatt at én måned har 30 døgn.
Oppgave 4
| Figur nr | Formel | Antall sirkler |
|---|---|---|
| $1$ | $2\cdot (2\cdot 2) -1$ | $7$ |
| $2$ | $2\cdot (3\cdot 3) -1$ | $17$ |
| $3$ | $2\cdot (4\cdot 4)-1$ | $31$ |
| $4$ | $2\cdot(5\cdot 5)-1$ | $29$ |
| $9$ | $2\cdot(10\cdot 10)-1$ | $199$ |
| $n$ | $2\cdot (n+1)^2-1= 2\cdot (n^2+2n+1)-1=2n^2+4n+1$ |
a)
Det vil være 29 sirkler i figur 4 og 199 sirkler i figur 9.
b)
Mønsteret er slik det er vist i tabellen øverst i svaret. Antall sirkler i figur n er $2n^2+4n+1$.
DEL 2
Oppgave 1
a)
Hytta koster 18 000 kroner å leie, og det kan være fra 1 til 12 personer på hytta.
b)
Skjæringspunktet mellom grafen til H og den rette linjen y=2250 er (8,2250). Det betyr at dersom 8 venner leier hytta sammen, må hver av dem betale 2250 kroner hver.
c)
Stigningstallet til den rette linjen som går gjennom punktene (6,H(6)) og (12,H(12)) er -250. Det betyr at fra 6 til 12 personer som leier hytta sammen, går prisen per person gjennomsnittlig ned med 250 kroner per ekstra person som er med på å dele leien.
Oppgave 2
a)
$5,4 - 5,15 = 0,25$
Renten er 0,25 prosentpoeng høyere dersom hun velger 1 år i stedet for 3 måneder.
$\frac{0,25}{5,15}\cdot 100=4,85$
Renten er 4,85 % høyere dersom hun velger 1 år i stedet for 3 måneder.
b)
$450\,000\cdot\frac{5,4}{100}=24300$
Malin får 24 300 kroner i renteinntekter dersom hun velger å binde pengene i 1 år.
Oppgave 3
a)
Bruker Geogebra til å finne statistikk for Solveigs skiturer:
I gjennomsnitt brukte Solveig 7,15 timer per skitur, mens Miriam brukte 4,7 timer per skitur. Gjennomsnittlig varte altså skiturene til Solveig lengre.
Medianen for Solveigs skiturer var 7,5 timer, mot 4 timer for Miriam. Det vil si at halvparten av skiturene til Solveig varte mer enn 7,5 timer, mens halvparten av skiturene til Miriam varte mer enn 4 timer.
Standardavviket for Solveigs skiturer er ca. 2,5 timer, med for Miriam er det 4,2. Det vil si at Miriam har større variasjon i varigheten på skiturene. Hun kan ha hatt noen veldig korte og noen veldig lange skiturer. Solveig holder seg nærmere gjennomsnittsvarigheten på sine skiturer.
Miriam har et gjennomsnitt som er høyere enn medianen, som vil si at hun har en eller flere lange skiturer som "drar opp" gjennomsnittet.
Solveig har et gjennomsnitt som er lavere enn medianen, som vil si at hun har en eller flere korte skiturer som "drar ned" gjennomsnittet.
b)
1) I den andre raden i tabellen står det at jentene gikk 11 skiturer på 3 timer eller mindre. I den tredje raden i tabellen står det at jentene gikk 14 skiturer på 5 timer eller mindre. Det må bety at 3 av skiturene var på 5 timer.
2) Vi ser av tallene over oppgave a) at Solveig gikk fire skiturer på 8 timer. Tabellen i oppgave b) viser at jentene bare gikk tre skiturer på 8 timer sammen. Det vil si at Miriam ikke var med på én av 8-timers turene til Solveig.
Oppgave 4
a)
Tuva kan ha brukt eksponentiell regresjonsanalyse, som vist under i Geogebra.
I modellen $f(x)=5244\cdot1,35^x$ vekstfaktoren 1,35, som betyr en månedlig vekst på 35 % følgere.
b)
Jeg forstår spørsmålet som at antall følgere skal øke med 40 % fra april til mai, og med 45 % fra mai til juni.
Antall følgere i mai: $24008\cdot 1,40 \approx 33611$
Antall følgere i juni: $33611\cdot 1,45 \approx 48736$
c)
Jeg løser oppgaven i Excel.
Tuva vil ha 42 % prosent flere følgere i august 2024 dersom hun klarer å nå det nye målet sitt for hver måned, sammenliknet med om økningen fortsetter å være på 35 % hver måned.
Oppgave 5
Påstand 1: "80 elever brukte mindre enn 40 minutter på lekser denne ettermiddagen."
Vi ser på første søyle i histogrammet, og ganger klassebredden med høyden på søylen: $40 \cdot 2 = 80$. Dette gir oss en frekvens på 80 stykker i klassen 0-40 minutter med lekser. Påstanden er riktig.
Påstand 2: "Den relative frekvensen for 100–150 minutter brukt på lekser er 1/5."
Vi finner frekvensen for alle søylene til sammen: $40\cdot 2 + 20\cdot 6 + 40\cdot 5 + 50\cdot 2 = 80+120+200+100 = 500$
Frekvensen for klassen 100-150 minutter er 100.
Den relative frekvensen for klassen 100-150 minutter er da 100 / 500 = 1/5. Påstanden er riktig.
Påstand 3: "Elevene som brukte mindre enn 60 minutter på leksene, brukte i gjennomsnitt 38 minutter."
80 elever brukte 0-40 minutter (gjennomsnittlig 20 minutter) og 120 elever brukte 40-60 minutter (gjennomsnittlig 50 minutter) på lekser.
$\frac{80\cdot 20 + 120\cdot 50}{200} = \frac{7600\, min}{200\, elever}=38 \, min/elev$. Påstanden er riktig.
Påstand 4: "For elevene som brukte mindre enn 60 minutter på leksene, er medianen for antall minutter høyere enn gjennomsnittet for antall minutter."
80 elever brukte 0-40 minutter og 120 elever brukte 40-60 minutter på lekser. Det er 200 elever til sammen i disse to klassene, og det betyr at medianelevene nr. 100 og 101 er i klassen 40-60 minutter. Medianen er altså mer enn gjennomsnittet (38 minutter). Påstanden er riktig.
Oppgave 6
Linje 1: variabelen "innskudd" settes lik 27 500 (kroner). Det er hvor mye Thea kan sette inn på BSU-kontoen hvert år.
Linje 2: variabelen "prosent_rente" settes lik 6,8 (%). Det er renten på BSU-kontoen.
Linje 3: variabelen "BSU" settes lik 0. Det er hvor mye hun har på BSU-kontoen. Før hun begynner sparingen, er det 0 kroner.
Linje 5: en for-løkka skal gå fra og med 2024 til (men ikke med) 2034. All koden linje 7-13 gjentas altså 10 ganger, som tilsvarer 10 år med sparing.
Linje 7: beløpet på BSU-kontoen oppdateres med nytt innskudd.
Linje 9: årets renter beregnes.
Linje 11: beløpet på BSU-kontoen oppdateres med årets renter.
Linje 13: året, årets renter og beløpet på BSU-kontoen skrives ut.
Totalt sett vil programmet skrive ut året, årets renter, og beløpet på BSU-kontoen for hvert år fra 2024 til og med 2033. Jeg antar at Thea vil finne ut hvor mye hun har på BSU-kontoen etter 10 år med årlig sparing.
Oppgave 7
Bruker Excel til å lage diagrammer.
Til venstre i bildet et linjediagram over utviklingen av antall lærlinger i Oslo og Rogaland fra 2018 til 2022.
Til høyre i bildet et stolpediagram over antall lærlinger i Oslo, Rogaland og hele Norge fra 2018 til 2022.
Antall lærlinger i Oslo har økt med $\frac{3779-3626}{3626}\cdot 100=4,8$ % fra 2018 til 2022.
Antall lærlinger i Rogaland har økt med $\frac{5960-5009}{5009}\cdot 100=19$ % fra 2018 til 2022. Det er en mye større økning enn i Oslo!
Antall lærlinger i Norge har økt med $\frac{48400-43322}{43322}\cdot 100=11,7$ % fra 2018 til 2022. Det vil si at antall lærlinger i Oslo har økt mindre enn landsgjennomsnittet, mens antall lærlinger i Rogaland har økt mer enn landsgjennomsnittet.
I 2022 utgjorde antall lærlinger i Oslo $\frac{3799}{48400}\cdot 100 = 7,9$ % av Norges lærlinger.
I 2022 utgjorde antall lærlinger i Rogaland $\frac{5960}{48400}\cdot 100 = 12,3$ % av Norges lærlinger.
Her er det bare fantasien og tiden som setter grenser for hvor mange diagrammer og beregninger man kan gjøre...