Løsning del 1 10kl Vår 24: Forskjell mellom sideversjoner
| (7 mellomliggende versjoner av en annen bruker er ikke vist) | |||
| Linje 56: | Linje 56: | ||
1: Usann, de bruker mest tid på sosiale medier. | 1: Usann, de bruker mest tid på sosiale medier. | ||
2: | 2: Usann | ||
3: Sann, (mangler 3 prosentpoeng) | 3: Sann, (mangler 3 prosentpoeng) | ||
4: | 4: Usann | ||
==Oppgave 4== | ==Oppgave 4== | ||
Begge endepunktene ligger på grafen, så da bruker vi disse verdiene. Stigningstallet er endring i y verdi, delt på endring i x verdi: | |||
$a = \frac{\Delta y}{\Delta x} = \frac{169 - 145}{16-10}= \frac{24}{6} = 4$ | |||
==Oppgave 5== | ==Oppgave 5== | ||
Løsningen er ikke riktig fordi han deler endringen på den nye verdien. Dersom han deler på den opprinnelige (gamle) verdien får han 10% som er riktig svar. | |||
==Oppgave 6== | ==Oppgave 6== | ||
Litt uklar oppgave, men jeg forutsetter at man kan velge størrelse på boksen selv. Jeg liker store matbokser og velger derfor: | |||
Bredde: b= 15 cm | |||
Høyde: h=10cm | |||
Lengde l = 20cm | |||
Dette er innvendige mål og volumet av boksen blir da: | |||
$V = b \cdot h \cdot l = 15cm \cdot 10 cm \cdot 20 cm = 3000cm ^3 = 3 dm^3$ | |||
Volumet av matboksen er 3 liter, eller tre kubikk desimeter. | |||
Forklar valgene?? Denne boksen er stor nok til to store skiver (halve) på grunnflaten, og 3 eller fire lag i høyden. Da blir jeg mett. | |||
==Oppgave 7== | ==Oppgave 7== | ||
[[File:070624-0.png|400px]] | |||
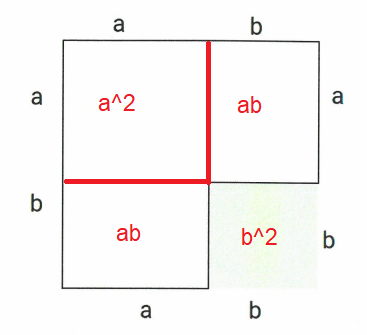
Vi ser fra tegningen at hytta kan deles i tre seksjoner som er: | |||
$a^2 + ab + ab = a^2 + 2ab$ | |||
Dersom man ønsker å ga mer algebraisk til verks kan man finne arealet av hytte pluss plen, og så trekke fra arealet av plenen etterpå: | |||
$(a+b)(a+b) - b \cdot b = a^2+2ab+ b^2-b^2 = a^2 + 2ab$ | |||
Siste sideversjon per 25. sep. 2024 kl. 08:04
Diskusjon av oppgaven på matteprat
DEL EN
Oppgave 1
Vi kaller pris voksen for y.
Pris barn, x
Vi får da to likninger basert på bildene (informasjonen):
x + 2y = 400
x + y = 260
Her skal vi bare finne x , prisen på barnebilletten og kan bruke innsettingsmetoden.
Fra den andre likningen får vi at y = 260 - x. Det setter vi inn for y i den første likningen og får en likning med bare x:
x + 2(260 - x) = 400
x + 520 - 2x = 400
-x = 400 - 520
-x = -120
Ganger begge sider med minus 1 og får x = 120
Prisen på barnebillett er 120 kroner.
Oppgave 2
På denne type oppgaver ser vi etter systemer. Vi ser at bredden på rektangelet har like mange kvadrater som figurnummeret og lengden er en mer enn figurnummeret.
a)
Litt unøyaktig tegnet, men de små røde firkanten er kvadrater.
b)
Som vi var inne på, bredden av rektangelet er det samme som figurtallet, og lengden av rektangelet er figurtallet pluss en. Dersom vi kanner figurtallet for n får vi:
$Antall ruter (n) = n (n+1) = n^2+n$
Oppgave 3
1: Usann, de bruker mest tid på sosiale medier.
2: Usann
3: Sann, (mangler 3 prosentpoeng)
4: Usann
Oppgave 4
Begge endepunktene ligger på grafen, så da bruker vi disse verdiene. Stigningstallet er endring i y verdi, delt på endring i x verdi:
$a = \frac{\Delta y}{\Delta x} = \frac{169 - 145}{16-10}= \frac{24}{6} = 4$
Oppgave 5
Løsningen er ikke riktig fordi han deler endringen på den nye verdien. Dersom han deler på den opprinnelige (gamle) verdien får han 10% som er riktig svar.
Oppgave 6
Litt uklar oppgave, men jeg forutsetter at man kan velge størrelse på boksen selv. Jeg liker store matbokser og velger derfor:
Bredde: b= 15 cm Høyde: h=10cm Lengde l = 20cm
Dette er innvendige mål og volumet av boksen blir da:
$V = b \cdot h \cdot l = 15cm \cdot 10 cm \cdot 20 cm = 3000cm ^3 = 3 dm^3$
Volumet av matboksen er 3 liter, eller tre kubikk desimeter.
Forklar valgene?? Denne boksen er stor nok til to store skiver (halve) på grunnflaten, og 3 eller fire lag i høyden. Da blir jeg mett.
Oppgave 7
Vi ser fra tegningen at hytta kan deles i tre seksjoner som er:
$a^2 + ab + ab = a^2 + 2ab$
Dersom man ønsker å ga mer algebraisk til verks kan man finne arealet av hytte pluss plen, og så trekke fra arealet av plenen etterpå:
$(a+b)(a+b) - b \cdot b = a^2+2ab+ b^2-b^2 = a^2 + 2ab$