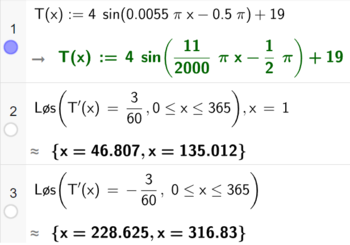R2 2024 vår LØSNING: Forskjell mellom sideversjoner
m La til løsningsforslag |
|||
| (67 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 4: | Linje 4: | ||
[https://lektorseland.no/L%C3%B8sningsforslag/Eksamen_R2_V24_L%C3%B8sning_Lektor_Seland.pdf Løsningsforslag Lektor Seland] | [https://lektorseland.no/L%C3%B8sningsforslag/Eksamen_R2_V24_L%C3%B8sning_Lektor_Seland.pdf Løsningsforslag Lektor Seland] | ||
=DEL 1= | |||
==Oppgave 1== | |||
$f(x)=-x^3+3x$ | |||
===a)=== | |||
$\int_{-1}^{0} f(x) dx = \int_{-1}^{0} (-x^3+3x) dx $ | |||
$=[-\frac14x^4+\frac32x^2]_{-1}^{0} $ | |||
$=0-(-\frac14+\frac32)$ | |||
$=\frac14-\frac64$ | |||
$=-\frac54$ | |||
===b)=== | |||
Finner nullpunktene til f: | |||
$-x^3+3x=0$ | |||
$-x(x^2-3)=0$ | |||
$-x(x+\sqrt{3})(x-\sqrt{3})$ | |||
Nullpunkter: $x=-\sqrt3, x=0, x=\sqrt 3$ | |||
Vi har ingen nullpunkter i intervallene $[-1,0\rangle$ og $\langle0,1]$ | |||
Beregner arealet av området avgrenset av grafen til f, x-aksen og linjene x=0 og x=1: | |||
$\int_{0}^{1} f(x) dx = \int_{0}^{1} (-x^3+3x) dx $ | |||
$=[-\frac14x^4+\frac32x^2]_{0}^{1} $ | |||
$=(-\frac14+\frac32)-0$ | |||
$=-\frac14+\frac64$ | |||
$=\frac54$ | |||
Samlet areal er summen av arealene i intervallene $[-1,0]$ og $[0,1]$ | |||
$A=|-\frac54|+\frac54=\frac{10}{4}=\frac52=2,5$ | |||
Arealet av området som er avgrenset av grafen til f, x-aksen og | |||
linjene x = −1 og x = 1 er 2,5. | |||
==Oppgave 2== | |||
Setter $u = sin(x)$. Da er $u'=cos(x)$ | |||
$u'=\frac{du}{dx}\Rightarrow dx = \frac{du}{u'}$ | |||
$\int sin^3(x)\cdot cos(x)dx$ | |||
$=\int u^3 \cdot u' \frac{du}{u'}$ | |||
$=\int u^3 du$ | |||
$=\frac14 u^4 + C$ | |||
$=\frac14 sin^4(x)+C$ | |||
==Oppgave 3== | |||
===a)=== | |||
Eleven prøver å finne hvor mange ledd det trengs i en rekke før summen av rekken blir større enn 200. Hvert ledd er gitt ved $a_n=4n-2$, og første ledd har n=1. | |||
===b)=== | |||
Vi har en aritmetisk rekke, fordi differansen mellom hvert ledd alltid er den samme (4 i dette tilfellet). Summen av en aritmetisk rekke er gitt ved $S=n\cdot\frac{a_1+a_n}{2}$ | |||
$n\cdot\frac{2+(4n-2)}{2}=200$ | |||
$\frac{4n^2}{2}=200$ | |||
$2n^2=200$ | |||
$n=\sqrt{100}$ (ingen negativ løsning fordi vi ser etter et positivt antall ledd) | |||
$n=10$ | |||
Eleven får skrevet ut verdien 10, som vil si at det summen av de 10 første leddene i rekken er 200 eller mer. | |||
==Oppgave 4== | |||
===a)=== | |||
$\vec{AC}=[2-1,0-1,-1-0]=[1,-1,-1]$ | |||
$\vec{AB}=[4-1,1-1,1-0]=[3,0,1]$ | |||
$\vec{AC} \times \vec{AB} = [1,-1,-1]\times[3,0,1]$ | |||
$=\begin{vmatrix} | |||
\vec i & \vec j & \vec k\\ | |||
1 & -1 & -1\\ | |||
3 & 0 & 1 | |||
\end{vmatrix}$ | |||
$=-\vec i -4\vec j +3\vec k$ | |||
$= [-1,-4,3]$ | |||
Arealet av paralellogrammet utspent av $\vec{AC}$ og $\vec{AB}$: | |||
$|[-1,-4,3]|=\sqrt{(-1)^2+(-4)^2+3^2}=\sqrt{26}$ | |||
Arealet av trekant ABC: | |||
$\frac{\sqrt{26}}{2}$ | |||
===b)=== | |||
$h=\frac{|\vec{AC}\times\vec{AB}|}{|\vec{AB}|}=\frac{\sqrt{26}}{\sqrt{3^2+0^2+1^2}}=\frac{\sqrt{26}}{\sqrt{10}}=\sqrt{\frac{13}{5}}$ | |||
===c)=== | |||
Vi har allerede normalvektoren for planet, gitt ved $\vec{AC} \times \vec{AB} = [-1,-4,3]$. Bruker punktet $P(-2,1,4)$ for å få en parameterfremstilling av linja. | |||
$l=\begin{cases} | |||
x = -2-t \\ | |||
y = 1-4t \\ | |||
z = 4 + 3t | |||
\end{cases}$ | |||
===d)=== | |||
Vi har $P(-2,1,4), \, \vec{n}_\alpha=[-1,-4,3], \, D(0,0,z)$ | |||
Retningsvektoren til planet står 90 grader på planet. Den vil altså også stå 90 grader på en linje m som er parallell til planet. Skalarproduktet mellom retningsvektoren til planet og retningsvektoren til linja m må være lik 0. | |||
Retningsvektor til linja m: $\vec{PD}=[0-(-2),0-1,z-4]=[2,-1,z-4]$ | |||
$\vec{PD}\cdot\vec{n}_\alpha=0$ | |||
$[2,-1,z-4]\cdot[-1,-4,3]=0$ | |||
$2\cdot(-1)+(-1)\cdot(-4)+(z-4)\cdot 3=0$ | |||
$-2+4+3z-12=0$ | |||
$3z=12+2-4$ | |||
$z=\frac{10}{3}$ | |||
Vi har $D(0,0,\frac{10}{3})$ | |||
==Oppgave 5== | |||
$f(x)=2\cdot sin(\frac{\pi}{6}x-\frac{\pi}{3})-1,\quad D_f=\langle0,20\rangle$ | |||
===a)=== | |||
$f(x)=0$ | |||
$2\cdot sin(\frac{\pi}{6}x-\frac{\pi}{3})-1=0$ | |||
$sin(\frac{\pi}{6}x-\frac{\pi}{3})=\frac 12$ | |||
$\frac{\pi}{6}x-\frac{\pi}{3}=\frac{\pi}{6}+k\cdot 2\pi \quad \vee \quad \frac{\pi}{6}x-\frac{\pi}{3}=\frac{5\pi}{6}+k\cdot 2\pi$ | |||
$\frac{\pi}{6}x=\frac{3\pi}{6}+k\cdot 2\pi \quad \vee \quad \frac{\pi}{6}x=\frac{7\pi}{6}+k\cdot2\pi$ | |||
$x=3+12k \quad \vee \quad x=7+12k$ | |||
Siden $D_f=\langle0,20\rangle$, har vi $x=3 \vee x=7 \vee x=15 \vee x=19$. | |||
===b)=== | |||
Generelt har vi $f(x)=A sin(kx+\phi)+d$ | |||
Amplituden er $A=2$ | |||
Likevektslinja er $d=-1$ | |||
Periode: $p=\frac{2\pi}{k}=\frac{2\pi}{\frac{\pi}{6}}=12$ | |||
Forskyvning langs likevektslinja: $x_f=-\frac{\phi}{k}=-\frac{-\frac{\pi}{3}}{\frac{\pi}{6}}=2$ | |||
=DEL 2= | |||
==Oppgave 1== | |||
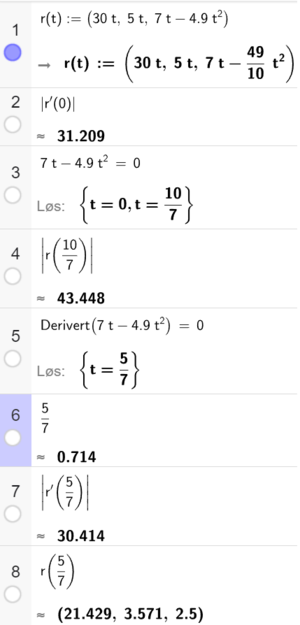
Bruker CAS i Geogebra. | |||
[[File: R2_V24_del2_1.png|300px]] | |||
===a)=== | |||
Farten til ballen idet den blir skutt (etter 0 sekunder) er ca. 31,2 m/s. Se linje 2 i CAS. | |||
===b)=== | |||
Vi finner tidene for når ballen er på bakken, det vil si når z-koordinaten til posisjonsvektoren er lik 0. Det er etter 0 sekunder (fraspark) og 10/7 sekunder (når ballen lander igjen). Se linje 3 i CAS. Vi finner posisjonen etter 10/7 sekunder. Se linje 4 i CAS. | |||
Ballen er ca. 43,4 meter fra hjørnemerket når den treffer fotballbanen igjen. | |||
===c)=== | |||
Vi finner tiden når ballen er på sitt høyeste, det vil si toppunktet til z-koordinaten til posisjonsvektoren. Ballen er på sitt høyeste etter 5/7 sekunder (se linje 5 i CAS). | |||
Farten er da 30,4 m/s (se linje 7 i CAS). | |||
Høyden til ballen er da 2,5 meter over bakken (se på z-koordinaten på linje 8 i CAS). | |||
==Oppgave 2== | |||
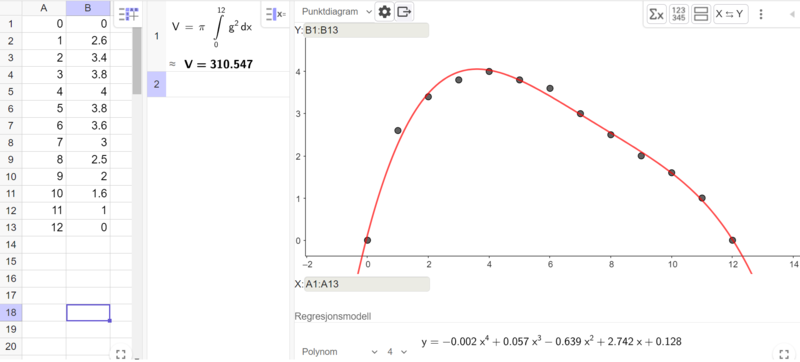
Jeg antar at vi skal finne volumet av hele pæra. Vi skal i så fall finne volumet av et omdreiningslegeme. | |||
$V=\pi\int_{x_1}^{x_2}(f(x)^2)dx$ | |||
Vi leser av bildet i oppgaven at $x_1=0$ og $x_2=12$. | |||
Jeg leser at koordinatene til 13 punkter, og bruker regresjon i Geogebra til å finne en omtrentlig funksjon for "kanten" av pæra. Jeg velger en 4.grads polynom, som passer best til punktene, og eksporterer funksjonen til grafikkfeltet. Der får den navnet g. Bruker deretter CAS til å finne volumet av hele pæra. | |||
[[File: R2_V24_del2_2.png|800px]] | |||
Pæra har et omtrentlig volum på 310 kubikkcentimeter. | |||
==Oppgave 3== | |||
$T(x)=4\cdot sin(0,0055\pi\cdot x-0,5\pi)+19$ | |||
===a)=== | |||
Likevektslinja er på y = 19. Det vil si at tidspunktet for når lyset slår seg på varierer om denne likevektslinja som viser kl. 19:00. | |||
Amplituden er 4, det vil si at lyset varierer med å slå seg på pluss/minus 4 timer fra klokka 19. Altså mellom kl. 15:00 og 23:00, som det står i oppgaven. | |||
Perioden er $\frac{2\pi}{0,0055\pi}\approx 364$. Det vil si at det i løpet av 364 dager (ca. et år) går T(x) gjennom én periode. I 6 måneder vil lyset slå seg på senere enn kl.19, og i 6 måneder vil lyset slå seg på tidligere enn kl. 19. | |||
Forskyvning langs likevektslinja er $-\frac{0,5\pi}{0,0055\pi}\approx 90$. Det vil si en forskyvning på 90 dager, som passer med antall dager i januar, februar og mars. Det vil si at 1. april slår lyset seg på kl. 19:00 (likevektslinja). | |||
===b)=== | |||
Bruker CAS i Geogebra. | |||
[[File: R2_V24_del2_3b.png|350px]] | |||
Lyset slår seg på 3 minutter senere per dag på dag nr. 46 og 135. Det er ca. 15. februar og 15. april. | |||
Lyset slår seg på 3 minutter tidligere per dag på dag nr. 228 og 316. Det er ca. 16. juli og 12. november. | |||
===c)=== | |||
[[File: R2_V24_del2_3c.png|300px]] | |||
Tidspunktet endrer seg raskest på dag 90 og 272. Det er 30. mars og 29. september. Tidspunktet endrer seg da med 4.14 minutter per dag. | |||
==Oppgave 4== | |||
===a)=== | |||
$a_n=n^3$ | |||
$a_{n+1}=(n+1)^3$ | |||
Rekursiv formel for summen av rekken: | |||
$S_{n+1}=S_n+a_{n+1}=S_n+(n+1)^3$ | |||
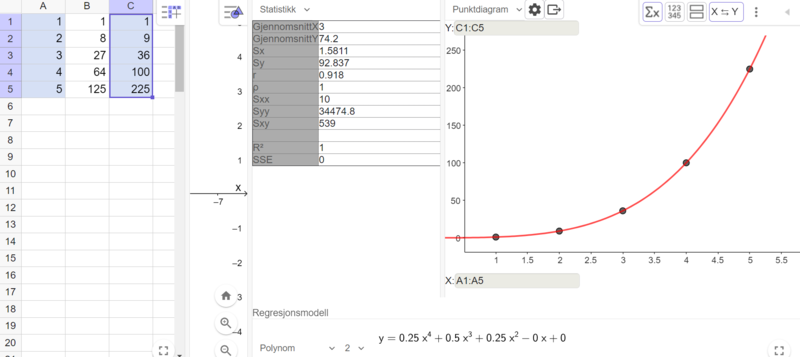
Eksplisitt formel for summen av rekken, finner vi ved regresjon i Geogebra: | |||
$S_n=0,25n^4+0,5n^3+0,25n^2$ | |||
[[File: R2_V24_del2_4a.png|800px]] | |||
===b)=== | |||
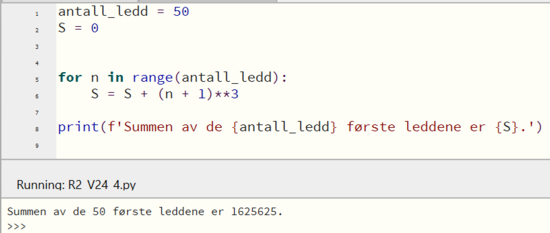
[[File: R2_V24_del2_4b_2.png|550px]] | |||
$S_{50}=1\,625\,625$ | |||
===c)=== | |||
Vi skal bevise $S_n: 1^3+2^3+3^3+...+n^3=0,25n^4+0,5n^3+0,25n^2$ | |||
[[File: R2_V24_del2_4c2.png|300px]] | |||
Vi sjekker først om formelen stemmer for n=1 (se linje 2 i CAS). Formelen stemmer for n=1, siden $S_1=1^3=1$. | |||
Vi antar nå at formelen stemmer for n = k, og sjekker om formelen stemmer for n = k + 1. Da vil $S_{k+1}=1^3+2^3+3^3+...+k^3+(k+1)^3=S_k+(k+1)^3$. Se linje 3 og 4 i CAS. | |||
Vi har nå vist at dersom formelen stemmer for n=k , må den også stemme for n=k+1. Siden formelen stemmer for n=1, stemmer den for n=2, osv. $S_k\Rightarrow S_{k+1}$. | |||
==Oppgave 5== | |||
Bruker CAS i Geogebra. | |||
[[File: R2_V24_del2_5_2.png |250px]] | |||
===a)=== | |||
Den minste avstanden fra kuleflaten til planet er $4-\sqrt 6 \approx 1,55$. Se linje 1-7 i CAS. | |||
===b)=== | |||
Planet $\alpha: x+2y+2z=-10$ | |||
Se linje 8-9 i CAS. | |||
==Oppgave 6== | |||
Øverste skjermbilde av CAS: hvordan man skriver inn S(x). Nesterste skjermbilde: hvordan det ser ut etter man trykker Enter. | |||
[[File: R2_V24_del2_6.png|350px]] | |||
Siden $S(x)=a_1 \cdot e^x$, gir x=0 den minste summen. Da må $a_1=1$. | |||
Siste sideversjon per 19. jul. 2024 kl. 11:00
Diskusjon av oppgaven på matteprat
DEL 1
Oppgave 1
$f(x)=-x^3+3x$
a)
$\int_{-1}^{0} f(x) dx = \int_{-1}^{0} (-x^3+3x) dx $
$=[-\frac14x^4+\frac32x^2]_{-1}^{0} $
$=0-(-\frac14+\frac32)$
$=\frac14-\frac64$
$=-\frac54$
b)
Finner nullpunktene til f:
$-x^3+3x=0$
$-x(x^2-3)=0$
$-x(x+\sqrt{3})(x-\sqrt{3})$
Nullpunkter: $x=-\sqrt3, x=0, x=\sqrt 3$
Vi har ingen nullpunkter i intervallene $[-1,0\rangle$ og $\langle0,1]$
Beregner arealet av området avgrenset av grafen til f, x-aksen og linjene x=0 og x=1:
$\int_{0}^{1} f(x) dx = \int_{0}^{1} (-x^3+3x) dx $
$=[-\frac14x^4+\frac32x^2]_{0}^{1} $
$=(-\frac14+\frac32)-0$
$=-\frac14+\frac64$
$=\frac54$
Samlet areal er summen av arealene i intervallene $[-1,0]$ og $[0,1]$
$A=|-\frac54|+\frac54=\frac{10}{4}=\frac52=2,5$
Arealet av området som er avgrenset av grafen til f, x-aksen og linjene x = −1 og x = 1 er 2,5.
Oppgave 2
Setter $u = sin(x)$. Da er $u'=cos(x)$
$u'=\frac{du}{dx}\Rightarrow dx = \frac{du}{u'}$
$\int sin^3(x)\cdot cos(x)dx$
$=\int u^3 \cdot u' \frac{du}{u'}$
$=\int u^3 du$
$=\frac14 u^4 + C$
$=\frac14 sin^4(x)+C$
Oppgave 3
a)
Eleven prøver å finne hvor mange ledd det trengs i en rekke før summen av rekken blir større enn 200. Hvert ledd er gitt ved $a_n=4n-2$, og første ledd har n=1.
b)
Vi har en aritmetisk rekke, fordi differansen mellom hvert ledd alltid er den samme (4 i dette tilfellet). Summen av en aritmetisk rekke er gitt ved $S=n\cdot\frac{a_1+a_n}{2}$
$n\cdot\frac{2+(4n-2)}{2}=200$
$\frac{4n^2}{2}=200$
$2n^2=200$
$n=\sqrt{100}$ (ingen negativ løsning fordi vi ser etter et positivt antall ledd)
$n=10$
Eleven får skrevet ut verdien 10, som vil si at det summen av de 10 første leddene i rekken er 200 eller mer.
Oppgave 4
a)
$\vec{AC}=[2-1,0-1,-1-0]=[1,-1,-1]$
$\vec{AB}=[4-1,1-1,1-0]=[3,0,1]$
$\vec{AC} \times \vec{AB} = [1,-1,-1]\times[3,0,1]$
$=\begin{vmatrix} \vec i & \vec j & \vec k\\ 1 & -1 & -1\\ 3 & 0 & 1 \end{vmatrix}$
$=-\vec i -4\vec j +3\vec k$
$= [-1,-4,3]$
Arealet av paralellogrammet utspent av $\vec{AC}$ og $\vec{AB}$:
$|[-1,-4,3]|=\sqrt{(-1)^2+(-4)^2+3^2}=\sqrt{26}$
Arealet av trekant ABC:
$\frac{\sqrt{26}}{2}$
b)
$h=\frac{|\vec{AC}\times\vec{AB}|}{|\vec{AB}|}=\frac{\sqrt{26}}{\sqrt{3^2+0^2+1^2}}=\frac{\sqrt{26}}{\sqrt{10}}=\sqrt{\frac{13}{5}}$
c)
Vi har allerede normalvektoren for planet, gitt ved $\vec{AC} \times \vec{AB} = [-1,-4,3]$. Bruker punktet $P(-2,1,4)$ for å få en parameterfremstilling av linja.
$l=\begin{cases} x = -2-t \\ y = 1-4t \\ z = 4 + 3t \end{cases}$
d)
Vi har $P(-2,1,4), \, \vec{n}_\alpha=[-1,-4,3], \, D(0,0,z)$
Retningsvektoren til planet står 90 grader på planet. Den vil altså også stå 90 grader på en linje m som er parallell til planet. Skalarproduktet mellom retningsvektoren til planet og retningsvektoren til linja m må være lik 0.
Retningsvektor til linja m: $\vec{PD}=[0-(-2),0-1,z-4]=[2,-1,z-4]$
$\vec{PD}\cdot\vec{n}_\alpha=0$
$[2,-1,z-4]\cdot[-1,-4,3]=0$
$2\cdot(-1)+(-1)\cdot(-4)+(z-4)\cdot 3=0$
$-2+4+3z-12=0$
$3z=12+2-4$
$z=\frac{10}{3}$
Vi har $D(0,0,\frac{10}{3})$
Oppgave 5
$f(x)=2\cdot sin(\frac{\pi}{6}x-\frac{\pi}{3})-1,\quad D_f=\langle0,20\rangle$
a)
$f(x)=0$
$2\cdot sin(\frac{\pi}{6}x-\frac{\pi}{3})-1=0$
$sin(\frac{\pi}{6}x-\frac{\pi}{3})=\frac 12$
$\frac{\pi}{6}x-\frac{\pi}{3}=\frac{\pi}{6}+k\cdot 2\pi \quad \vee \quad \frac{\pi}{6}x-\frac{\pi}{3}=\frac{5\pi}{6}+k\cdot 2\pi$
$\frac{\pi}{6}x=\frac{3\pi}{6}+k\cdot 2\pi \quad \vee \quad \frac{\pi}{6}x=\frac{7\pi}{6}+k\cdot2\pi$
$x=3+12k \quad \vee \quad x=7+12k$
Siden $D_f=\langle0,20\rangle$, har vi $x=3 \vee x=7 \vee x=15 \vee x=19$.
b)
Generelt har vi $f(x)=A sin(kx+\phi)+d$
Amplituden er $A=2$
Likevektslinja er $d=-1$
Periode: $p=\frac{2\pi}{k}=\frac{2\pi}{\frac{\pi}{6}}=12$
Forskyvning langs likevektslinja: $x_f=-\frac{\phi}{k}=-\frac{-\frac{\pi}{3}}{\frac{\pi}{6}}=2$
DEL 2
Oppgave 1
Bruker CAS i Geogebra.
a)
Farten til ballen idet den blir skutt (etter 0 sekunder) er ca. 31,2 m/s. Se linje 2 i CAS.
b)
Vi finner tidene for når ballen er på bakken, det vil si når z-koordinaten til posisjonsvektoren er lik 0. Det er etter 0 sekunder (fraspark) og 10/7 sekunder (når ballen lander igjen). Se linje 3 i CAS. Vi finner posisjonen etter 10/7 sekunder. Se linje 4 i CAS.
Ballen er ca. 43,4 meter fra hjørnemerket når den treffer fotballbanen igjen.
c)
Vi finner tiden når ballen er på sitt høyeste, det vil si toppunktet til z-koordinaten til posisjonsvektoren. Ballen er på sitt høyeste etter 5/7 sekunder (se linje 5 i CAS).
Farten er da 30,4 m/s (se linje 7 i CAS).
Høyden til ballen er da 2,5 meter over bakken (se på z-koordinaten på linje 8 i CAS).
Oppgave 2
Jeg antar at vi skal finne volumet av hele pæra. Vi skal i så fall finne volumet av et omdreiningslegeme.
$V=\pi\int_{x_1}^{x_2}(f(x)^2)dx$
Vi leser av bildet i oppgaven at $x_1=0$ og $x_2=12$.
Jeg leser at koordinatene til 13 punkter, og bruker regresjon i Geogebra til å finne en omtrentlig funksjon for "kanten" av pæra. Jeg velger en 4.grads polynom, som passer best til punktene, og eksporterer funksjonen til grafikkfeltet. Der får den navnet g. Bruker deretter CAS til å finne volumet av hele pæra.
Pæra har et omtrentlig volum på 310 kubikkcentimeter.
Oppgave 3
$T(x)=4\cdot sin(0,0055\pi\cdot x-0,5\pi)+19$
a)
Likevektslinja er på y = 19. Det vil si at tidspunktet for når lyset slår seg på varierer om denne likevektslinja som viser kl. 19:00.
Amplituden er 4, det vil si at lyset varierer med å slå seg på pluss/minus 4 timer fra klokka 19. Altså mellom kl. 15:00 og 23:00, som det står i oppgaven.
Perioden er $\frac{2\pi}{0,0055\pi}\approx 364$. Det vil si at det i løpet av 364 dager (ca. et år) går T(x) gjennom én periode. I 6 måneder vil lyset slå seg på senere enn kl.19, og i 6 måneder vil lyset slå seg på tidligere enn kl. 19.
Forskyvning langs likevektslinja er $-\frac{0,5\pi}{0,0055\pi}\approx 90$. Det vil si en forskyvning på 90 dager, som passer med antall dager i januar, februar og mars. Det vil si at 1. april slår lyset seg på kl. 19:00 (likevektslinja).
b)
Bruker CAS i Geogebra.
Lyset slår seg på 3 minutter senere per dag på dag nr. 46 og 135. Det er ca. 15. februar og 15. april.
Lyset slår seg på 3 minutter tidligere per dag på dag nr. 228 og 316. Det er ca. 16. juli og 12. november.
c)
Tidspunktet endrer seg raskest på dag 90 og 272. Det er 30. mars og 29. september. Tidspunktet endrer seg da med 4.14 minutter per dag.
Oppgave 4
a)
$a_n=n^3$
$a_{n+1}=(n+1)^3$
Rekursiv formel for summen av rekken:
$S_{n+1}=S_n+a_{n+1}=S_n+(n+1)^3$
Eksplisitt formel for summen av rekken, finner vi ved regresjon i Geogebra:
$S_n=0,25n^4+0,5n^3+0,25n^2$
b)
$S_{50}=1\,625\,625$
c)
Vi skal bevise $S_n: 1^3+2^3+3^3+...+n^3=0,25n^4+0,5n^3+0,25n^2$
Vi sjekker først om formelen stemmer for n=1 (se linje 2 i CAS). Formelen stemmer for n=1, siden $S_1=1^3=1$.
Vi antar nå at formelen stemmer for n = k, og sjekker om formelen stemmer for n = k + 1. Da vil $S_{k+1}=1^3+2^3+3^3+...+k^3+(k+1)^3=S_k+(k+1)^3$. Se linje 3 og 4 i CAS.
Vi har nå vist at dersom formelen stemmer for n=k , må den også stemme for n=k+1. Siden formelen stemmer for n=1, stemmer den for n=2, osv. $S_k\Rightarrow S_{k+1}$.
Oppgave 5
Bruker CAS i Geogebra.
a)
Den minste avstanden fra kuleflaten til planet er $4-\sqrt 6 \approx 1,55$. Se linje 1-7 i CAS.
b)
Planet $\alpha: x+2y+2z=-10$
Se linje 8-9 i CAS.
Oppgave 6
Øverste skjermbilde av CAS: hvordan man skriver inn S(x). Nesterste skjermbilde: hvordan det ser ut etter man trykker Enter.
Siden $S(x)=a_1 \cdot e^x$, gir x=0 den minste summen. Da må $a_1=1$.