S2 2024 vår LØSNING: Forskjell mellom sideversjoner
Ny side: [https://matematikk.net/matteprat/download/file.php?id=4948 Oppgaven som pdf] [https://matematikk.net/matteprat/viewtopic.php?f=13&t=54731 Diskusjon av oppgaven på matteprat] |
|||
| (4 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 2: | Linje 2: | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=54731 Diskusjon av oppgaven på matteprat] | [https://matematikk.net/matteprat/viewtopic.php?f=13&t=54731 Diskusjon av oppgaven på matteprat] | ||
[https://matematikk.net/matteprat/download/file.php?id=4955 Løsningsforslag av Ståle Gjelsten] | |||
=DEL 1= | |||
==Oppgave 1== | |||
$f(x)=-x^3+3x$ | |||
===a)=== | |||
$\int_{-1}^{0} f(x) dx = \int_{-1}^{0} (-x^3+3x) dx $ | |||
$=[-\frac14x^4+\frac32x^2]_{-1}^{0} $ | |||
$=0-(-\frac14+\frac32)$ | |||
$=\frac14-\frac64$ | |||
$=-\frac54$ | |||
===b)=== | |||
Finner nullpunktene til f: | |||
$-x^3+3x=0$ | |||
$-x(x^2-3)=0$ | |||
$-x(x+\sqrt{3})(x-\sqrt{3})$ | |||
Nullpunkter: $x=-\sqrt3, x=0, x=\sqrt 3$ | |||
Vi har ingen nullpunkter i intervallene $[-1,0\rangle$ og $\langle0,1]$ | |||
Beregner arealet av området avgrenset av grafen til f, x-aksen og linjene x=0 og x=1: | |||
$\int_{0}^{1} f(x) dx = \int_{0}^{1} (-x^3+3x) dx $ | |||
$=[-\frac14x^4+\frac32x^2]_{0}^{1} $ | |||
$=(-\frac14+\frac32)-0$ | |||
$=-\frac14+\frac64$ | |||
$=\frac54$ | |||
Samlet areal er summen av arealene i intervallene $[-1,0]$ og $[0,1]$ | |||
$A=|-\frac54|+\frac54=\frac{10}{4}=\frac52=2,5$ | |||
Arealet av området som er avgrenset av grafen til f, x-aksen og | |||
linjene x = −1 og x = 1 er 2,5. | |||
==Oppgave 3== | |||
===a)=== | |||
Eleven prøver å finne hvor mange ledd det trengs i en rekke før summen av rekken blir større enn 200. Hvert ledd er gitt ved $a_n=4n-2$, og første ledd har n=1. | |||
===b)=== | |||
Vi har en aritmetisk rekke, fordi differansen mellom hvert ledd alltid er den samme (4 i dette tilfellet). Summen av en aritmetisk rekke er gitt ved $S=n\cdot\frac{a_1+a_n}{2}$ | |||
$n\cdot\frac{2+(4n-2)}{2}=200$ | |||
$\frac{4n^2}{2}=200$ | |||
$2n^2=200$ | |||
$n=\sqrt{100}$ (ingen negativ løsning fordi vi ser etter et positivt antall ledd) | |||
$n=10$ | |||
Eleven får skrevet ut verdien 10, som vil si at det summen av de 10 første leddene i rekken er 200 eller mer. | |||
=DEL 2= | |||
==Oppgave 4== | |||
===a)=== | |||
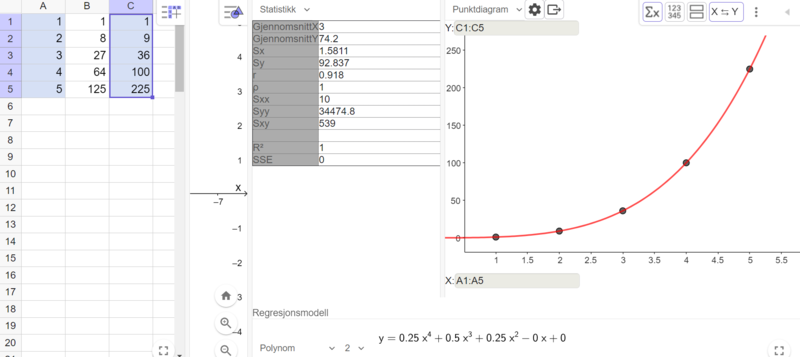
$a_n=n^3$ | |||
$a_{n+1}=(n+1)^3$ | |||
Rekursiv formel for summen av rekken: | |||
$S_{n+1}=S_n+a_{n+1}=S_n+(n+1)^3$ | |||
Eksplisitt formel for summen av rekken, finner vi ved regresjon i Geogebra: | |||
$S_n=0,25n^4+0,5n^3+0,25n^2$ | |||
[[File: R2_V24_del2_4a.png|800px]] | |||
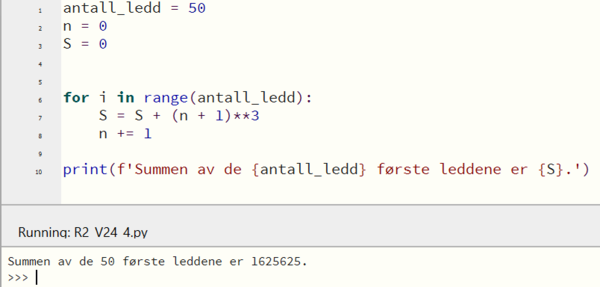
===b)=== | |||
[[File: R2_V24_del2_4b.png|600px]] | |||
Siste sideversjon per 13. jul. 2024 kl. 18:58
Diskusjon av oppgaven på matteprat
Løsningsforslag av Ståle Gjelsten
DEL 1
Oppgave 1
$f(x)=-x^3+3x$
a)
$\int_{-1}^{0} f(x) dx = \int_{-1}^{0} (-x^3+3x) dx $
$=[-\frac14x^4+\frac32x^2]_{-1}^{0} $
$=0-(-\frac14+\frac32)$
$=\frac14-\frac64$
$=-\frac54$
b)
Finner nullpunktene til f:
$-x^3+3x=0$
$-x(x^2-3)=0$
$-x(x+\sqrt{3})(x-\sqrt{3})$
Nullpunkter: $x=-\sqrt3, x=0, x=\sqrt 3$
Vi har ingen nullpunkter i intervallene $[-1,0\rangle$ og $\langle0,1]$
Beregner arealet av området avgrenset av grafen til f, x-aksen og linjene x=0 og x=1:
$\int_{0}^{1} f(x) dx = \int_{0}^{1} (-x^3+3x) dx $
$=[-\frac14x^4+\frac32x^2]_{0}^{1} $
$=(-\frac14+\frac32)-0$
$=-\frac14+\frac64$
$=\frac54$
Samlet areal er summen av arealene i intervallene $[-1,0]$ og $[0,1]$
$A=|-\frac54|+\frac54=\frac{10}{4}=\frac52=2,5$
Arealet av området som er avgrenset av grafen til f, x-aksen og linjene x = −1 og x = 1 er 2,5.
Oppgave 3
a)
Eleven prøver å finne hvor mange ledd det trengs i en rekke før summen av rekken blir større enn 200. Hvert ledd er gitt ved $a_n=4n-2$, og første ledd har n=1.
b)
Vi har en aritmetisk rekke, fordi differansen mellom hvert ledd alltid er den samme (4 i dette tilfellet). Summen av en aritmetisk rekke er gitt ved $S=n\cdot\frac{a_1+a_n}{2}$
$n\cdot\frac{2+(4n-2)}{2}=200$
$\frac{4n^2}{2}=200$
$2n^2=200$
$n=\sqrt{100}$ (ingen negativ løsning fordi vi ser etter et positivt antall ledd)
$n=10$
Eleven får skrevet ut verdien 10, som vil si at det summen av de 10 første leddene i rekken er 200 eller mer.
DEL 2
Oppgave 4
a)
$a_n=n^3$
$a_{n+1}=(n+1)^3$
Rekursiv formel for summen av rekken:
$S_{n+1}=S_n+a_{n+1}=S_n+(n+1)^3$
Eksplisitt formel for summen av rekken, finner vi ved regresjon i Geogebra:
$S_n=0,25n^4+0,5n^3+0,25n^2$