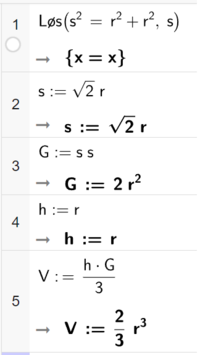R1 2024 Vår LØSNING: Forskjell mellom sideversjoner
m La til mitt løsningsforslag |
Ingen redigeringsforklaring |
||
| (31 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 4: | Linje 4: | ||
[https://lektorseland.no/Løsningsforslag/Eksamen_R1_V24_Løsning_Lektor_Seland.pdf Løsningsforslag fra Lektor Seland] | [https://lektorseland.no/Løsningsforslag/Eksamen_R1_V24_Løsning_Lektor_Seland.pdf Løsningsforslag fra Lektor Seland] | ||
==Oppgave 1== | |||
$f(x)=4x^2\cdot ln(3x)$ | |||
$f'(x)=8x\cdot ln(3x) + 4x^2 \cdot \frac{1}{3x}\cdot 3$ | |||
$f'(x)=8x\cdot ln(3x) + 4x$ | |||
==Oppgave 2== | |||
$(ln\,x)^2-lnx=6$ | |||
Setter $u=ln\,x$ | |||
$u^2-u-6=0$ | |||
$(u+2)(u-3)=0$ | |||
$u=-2 \vee u=3$ | |||
$ln\,x=-2 \vee ln\,x=3$ | |||
$x=e^{-2}\vee x=e^3$ | |||
$x=\frac{1}{e^2}\vee x=e^3$ | |||
==Oppgave 3== | |||
\[f(x)=e^{-x+1},\,D_f=\mathbb{R}\] | |||
\[ \lim_{x\to \infty} e^{-x+1}=e^{-\infty}=\frac{1}{e^{\infty}}=0\] | |||
\[ \lim_{x\to -\infty} e^{-x+1}=e^{\infty}=\infty\] | |||
Den siste grenseverdien går mot uendelig og eksisterer derfor ikke. | |||
==Oppgave 4== | |||
$A(3,4), \,B(-1,-2),\, C(3+t,2t)$ der $t\in\mathbb{R}$ | |||
===a)=== | |||
Bestemmer stigningstallet fra A til B: | |||
$a=\frac{4-(-2)}{3-(-1)}=\frac 64=\frac 32$ | |||
Stigningstallet fra A til C (eller B til C) skal være det samme. | |||
$\frac{2t-4}{3+t-3}=\frac 32$ | |||
$\frac{2t-4}{t}=\frac 32$ | |||
$4t-8=3t$ | |||
$t=8$ | |||
(Kunne også brukt at $\vec{AC}=k\cdot\vec{AB}$, som er litt mer "R1") | |||
===b)=== | |||
Skalarproduktet mellom vektorene som utspenner en 90 graders vinkel, skal være null. | |||
$\vec{AC}\cdot\vec{BC}=0$ | |||
$[3+t-3,2t-4]\cdot[3+t-(-1),2t-(-2)]=0$ | |||
$=[t,2t-4]\cdot[t+4,2t+2]=0$ | |||
$(t^2+4t)+(4t^2-4t-8)=0$ | |||
$5t^2-8=0$ | |||
$t=\pm\sqrt{\frac 85}$ | |||
==Oppgave 5== | |||
Vi endrer funksjons definisjonsområde til at 2 ikke er med i definisjonsmengden. : | |||
\[ f(x) = \begin{cases} | |||
\quad \quad x,\quad 0\leq x <2 \\ | |||
\, 5-x,\quad 2<x\leq 5 \\ | |||
\end{cases} \] | |||
Vi har ivaretatt alle kravene: | |||
$\bullet$ Verdimengden er uendret. | |||
$\bullet$ Definisjonsmengden er så stor som mulig (uten å endre verdimengden) | |||
$\bullet$ f er kontinuerlig. Vi sier at f er kontinuerlig hvis f er kontinuerlig for alle $a\in D_f$. Siden funksjonen f ikke er definert i punktet 2, så er f kontinuerlig i alle punkter i definisjonsmengden. | |||
For nærmere forklaring, se s.129-131 i Aschehougs bok "Matematikk S1". | |||
=DEL 2= | |||
==Oppgave 1== | |||
Bruker CAS i Geogebra. Oppgaven kan også løses grafisk i Geogebra. | |||
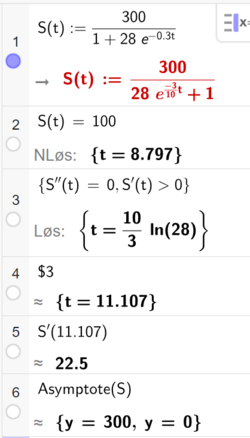
[[File: R1_V24_del2_1.png|250px]] | |||
===a)=== | |||
Det tar 8,8 dager før 100 elever er smittet (linje 2 i CAS). | |||
===b)=== | |||
Flest elever blir smittet etter 11,1 dager. Da blir 22,5 elever smittet per dag (linje 3-5 i CAS). | |||
===c)=== | |||
S har to asymptoter; y = 0 og y = 300 (linje 6 i CAS). Det angir henholdsvis minimum og maksimum antall smittede. Det var 0 smittede før epidemien, og det stopper på 300 smittede. | |||
==Oppgave 2== | |||
===a)=== | |||
$e^{k\cdot ln(x)}=e^{ln(x)\cdot k}=(e^{ln(x)})^k=x^k$ | |||
$ln(x)$ er ikke definert for $x\leq 0$. Påstanden er sann for $x>0$. | |||
===b)=== | |||
\[ \lim_{x\to 2^-} x^3-2=2^3-2=8-2=6\] | |||
\[ \lim_{x\to 2^+} 3x^2-4=3\cdot 2^2-4=12-4=8\] | |||
Funksjonen er ikke kontinuerlig i x=2, og er er derfor ikke deriverbar i x=2. Påstanden er usann. | |||
===c)=== | |||
"En funksjon har en omvendt funksjon hvis den vokser i hele sitt definisjonsområde, eller at den avtar i hele sitt definisjonsområde." (NDLA, 2024) | |||
En funksjon kan likevel ha delt forskrift, og være strengt voksende i det ene definisjonsområdet, og strengt avtagende i det andre definisjonsområdet. Funksjonen vi da kunne ha en omvendt funksjon med delt forskrift. | |||
Påstanden er sann. | |||
Les mer om dette her: https://ndla.no/nb/subject:1:734bd33b-da6d-49b0-bb34-c6df5b956f8e/topic:1:55aacc4a-0d06-446d-a2b5-9671657213c5/topic:1:5c533c1c-cb50-40b7-a7ef-578a263f9c9f/resource:b0967319-7807-47c8-9aa5-b65b9201fd8e | |||
==Oppgave 3== | |||
Bruker CAS i Geogebra. | |||
[[File: R1_V24_del2_3.png|300px]] | |||
===a)=== | |||
Avstanden i luftlinje mellom bilene etter 1 minutt er ca. 2 km (linje 3 i CAS). | |||
===b)=== | |||
Bil B har kjørt lengre på 10 sekunder enn bil A, så jeg antar at bil B er på motorveien (linje 4-5 i CAS). | |||
En annen måte å løse det på er å finne absoluttverdien av fartsvektoren (altså posisjonsvektoren derivert). Her ser vi at bil A har en fart på 1,12 km/min, mens bil B har en fart på 1,58 km/min (linje 6-7 i CAS). | |||
===c)=== | |||
Bil B har samme posisjon som bil A etter kortest tid, 8,6 minutter. Derfor kommer bil B til veikrysset først (linje 8-9 i CAS). | |||
==Oppgave 4== | |||
Bruker CAS i Geogebra. | |||
[[File: R1_V24_del2_4a.png|300px]] | |||
===a)=== | |||
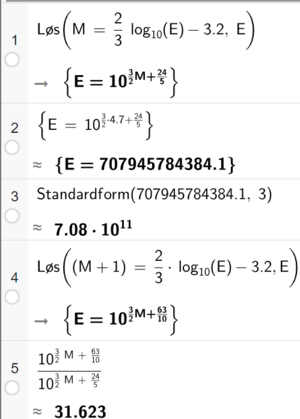
Se linje 1 i CAS for et uttrykket for E. | |||
Det løses ut $7,08\cdot 10^{11}$ joule i et jordskjelv som måler 4,7 på momentmagnitudeskalaen (linje 2-3 i CAS) | |||
===b)=== | |||
Det utløses ca. 31,6 ganger så stor er energien i et jordskjelv, dersom M øker med 1 (linje 4-5 i CAS). | |||
==Oppgave 5== | |||
===a)=== | |||
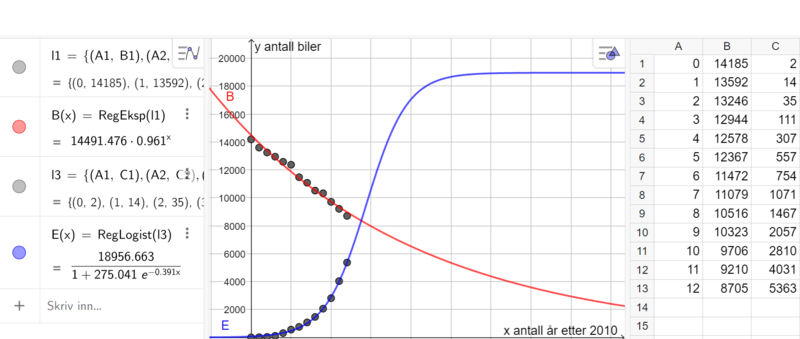
Jeg bruker regresjon i Geogebra til å velge modeller som passer godt til de datapunktene jeg har. Jeg velger en eksponentiell modell for antall bensinbiler. Her kunne en lineær modell også passet til datapunktene, men jeg velger en eksponentiell modell, siden jeg mener at antall bensinbiler ikke vil "stupe" til 0, men heller bli gradvis færre, og flate ut på et lavt antall. Jeg velger en logistisk modell for antall elbiler, da den både passer godt til datapunktene, og kan være en modell som passer noen år frem i tid. | |||
[[File: S1_V24_del2_6_2.png|800px]] | |||
===b)=== | |||
Modellen for bensinbiler foreslår en nedgang i antall bensinbiler på 4 % årlig. Jeg mener modeller kan passe i flere år etter 2022, for eksempel frem til 2050, siden mange bytter ut bensinbilen sin med elbil. En gang i fremtiden kan det være at ingen lenger eier en bensinbil, men vi vet ikke når det eventuelt vil skje. | |||
Modellen for elbiler kan passe i flere år etter 2022, f.eks. frem til 2030 eller 2040. Modellen viser at antall elbiler holder seg på samme antall fra ca. 2024. Det kan hende antall elbiler stabiliserer seg i Moss, men det kan også hende antallet fortsetter å øke (eller til og med synker!). Vi kan ikke vite det sikkert. Det kan komme færre fordeler og flere avgifter for elbiler - eller motsatt. Det er mye som spiller inn på hva slags bil folk velger. | |||
==Oppgave 6== | |||
===a)=== | |||
Lars prøver å finne ut størst mulig areal av det innskrevne rektangelet ABCD. | |||
Svaret blir ca. 3,08 hvis man kjører programmet, som betyr at det største mulige arealet til rektangel ABCD er 3,08. | |||
===b)=== | |||
Lars bruker definisjonen av den deriverte til å regne ut tilnærmet verdi av den deriverte i et punkt på funksjonen for areal av rektangelet (gitt i linje 4-5). Programmet gjør dette ved å regne ut stigningstallet i et veldig lite intervall (bredde 0,0001) på areal-funksjonen (linje 8-9). | |||
Programmet starter med å beregne den deriverte i x=0. Så lenge den deriverte av areal-funksjonen er større enn 0, altså areal-funksjonen er voksende, fortsetter programmet å regne den deriverte i neste lille intervall (x øker med 0,01 for hver runde). Når den deriverte ikke lenger er større enn 0, vil man ha funnet en tilnærmet x-verdi for toppunktet. Programmet skriver til slutt ut y-verdien i toppunktet av areal-funksjonen, altså det største mulige arealet til ABCD. | |||
Hvis målet er å finne toppunktet til en hvilken som helst funksjon, vil ikke strategien fungere dersom funksjonen ikke har noe toppunkt, og strategien vil heller ikke fungere hvis funksjonen er synkende fra x=0. | |||
==Oppgave 7== | |||
Pyramiden har størst volum dersom hjørnene i grunnflaten går helt ytterst til halvkulens overflate, og dersom høyden også går helt til halvkulens overflate. | |||
Bruker CAS i Geogebra. | |||
[[File: S1_V24_del2_8.png | 200 px]] | |||
I linje 1 finner vi lengden på siden til grunnflaten. Svaret på linje 1 hadde endret seg da skjermbildet ble tatt, men det sto opprinnelig sammen uttrykk for s som defineres i linje 2. | |||
I linje 3 beregnes arealet av grunnflaten. | |||
I linje 4 defineres høyden h til å være lik radiusen r. | |||
Volumet til den største mulige pyramiden er $V=\frac{2}{3}r^3$ (linje 5) | |||
Siste sideversjon per 28. okt. 2024 kl. 17:40
Diskusjon av oppgaven på matteprat
Løsningsforslag fra Lektor Seland
Oppgave 1
$f(x)=4x^2\cdot ln(3x)$
$f'(x)=8x\cdot ln(3x) + 4x^2 \cdot \frac{1}{3x}\cdot 3$
$f'(x)=8x\cdot ln(3x) + 4x$
Oppgave 2
$(ln\,x)^2-lnx=6$
Setter $u=ln\,x$
$u^2-u-6=0$
$(u+2)(u-3)=0$
$u=-2 \vee u=3$
$ln\,x=-2 \vee ln\,x=3$
$x=e^{-2}\vee x=e^3$
$x=\frac{1}{e^2}\vee x=e^3$
Oppgave 3
\[f(x)=e^{-x+1},\,D_f=\mathbb{R}\]
\[ \lim_{x\to \infty} e^{-x+1}=e^{-\infty}=\frac{1}{e^{\infty}}=0\]
\[ \lim_{x\to -\infty} e^{-x+1}=e^{\infty}=\infty\]
Den siste grenseverdien går mot uendelig og eksisterer derfor ikke.
Oppgave 4
$A(3,4), \,B(-1,-2),\, C(3+t,2t)$ der $t\in\mathbb{R}$
a)
Bestemmer stigningstallet fra A til B:
$a=\frac{4-(-2)}{3-(-1)}=\frac 64=\frac 32$
Stigningstallet fra A til C (eller B til C) skal være det samme.
$\frac{2t-4}{3+t-3}=\frac 32$
$\frac{2t-4}{t}=\frac 32$
$4t-8=3t$
$t=8$
(Kunne også brukt at $\vec{AC}=k\cdot\vec{AB}$, som er litt mer "R1")
b)
Skalarproduktet mellom vektorene som utspenner en 90 graders vinkel, skal være null.
$\vec{AC}\cdot\vec{BC}=0$
$[3+t-3,2t-4]\cdot[3+t-(-1),2t-(-2)]=0$
$=[t,2t-4]\cdot[t+4,2t+2]=0$
$(t^2+4t)+(4t^2-4t-8)=0$
$5t^2-8=0$
$t=\pm\sqrt{\frac 85}$
Oppgave 5
Vi endrer funksjons definisjonsområde til at 2 ikke er med i definisjonsmengden. :
\[ f(x) = \begin{cases} \quad \quad x,\quad 0\leq x <2 \\ \, 5-x,\quad 2<x\leq 5 \\ \end{cases} \]
Vi har ivaretatt alle kravene:
$\bullet$ Verdimengden er uendret.
$\bullet$ Definisjonsmengden er så stor som mulig (uten å endre verdimengden)
$\bullet$ f er kontinuerlig. Vi sier at f er kontinuerlig hvis f er kontinuerlig for alle $a\in D_f$. Siden funksjonen f ikke er definert i punktet 2, så er f kontinuerlig i alle punkter i definisjonsmengden.
For nærmere forklaring, se s.129-131 i Aschehougs bok "Matematikk S1".
DEL 2
Oppgave 1
Bruker CAS i Geogebra. Oppgaven kan også løses grafisk i Geogebra.
a)
Det tar 8,8 dager før 100 elever er smittet (linje 2 i CAS).
b)
Flest elever blir smittet etter 11,1 dager. Da blir 22,5 elever smittet per dag (linje 3-5 i CAS).
c)
S har to asymptoter; y = 0 og y = 300 (linje 6 i CAS). Det angir henholdsvis minimum og maksimum antall smittede. Det var 0 smittede før epidemien, og det stopper på 300 smittede.
Oppgave 2
a)
$e^{k\cdot ln(x)}=e^{ln(x)\cdot k}=(e^{ln(x)})^k=x^k$
$ln(x)$ er ikke definert for $x\leq 0$. Påstanden er sann for $x>0$.
b)
\[ \lim_{x\to 2^-} x^3-2=2^3-2=8-2=6\]
\[ \lim_{x\to 2^+} 3x^2-4=3\cdot 2^2-4=12-4=8\]
Funksjonen er ikke kontinuerlig i x=2, og er er derfor ikke deriverbar i x=2. Påstanden er usann.
c)
"En funksjon har en omvendt funksjon hvis den vokser i hele sitt definisjonsområde, eller at den avtar i hele sitt definisjonsområde." (NDLA, 2024)
En funksjon kan likevel ha delt forskrift, og være strengt voksende i det ene definisjonsområdet, og strengt avtagende i det andre definisjonsområdet. Funksjonen vi da kunne ha en omvendt funksjon med delt forskrift.
Påstanden er sann.
Oppgave 3
Bruker CAS i Geogebra.
a)
Avstanden i luftlinje mellom bilene etter 1 minutt er ca. 2 km (linje 3 i CAS).
b)
Bil B har kjørt lengre på 10 sekunder enn bil A, så jeg antar at bil B er på motorveien (linje 4-5 i CAS).
En annen måte å løse det på er å finne absoluttverdien av fartsvektoren (altså posisjonsvektoren derivert). Her ser vi at bil A har en fart på 1,12 km/min, mens bil B har en fart på 1,58 km/min (linje 6-7 i CAS).
c)
Bil B har samme posisjon som bil A etter kortest tid, 8,6 minutter. Derfor kommer bil B til veikrysset først (linje 8-9 i CAS).
Oppgave 4
Bruker CAS i Geogebra.
a)
Se linje 1 i CAS for et uttrykket for E.
Det løses ut $7,08\cdot 10^{11}$ joule i et jordskjelv som måler 4,7 på momentmagnitudeskalaen (linje 2-3 i CAS)
b)
Det utløses ca. 31,6 ganger så stor er energien i et jordskjelv, dersom M øker med 1 (linje 4-5 i CAS).
Oppgave 5
a)
Jeg bruker regresjon i Geogebra til å velge modeller som passer godt til de datapunktene jeg har. Jeg velger en eksponentiell modell for antall bensinbiler. Her kunne en lineær modell også passet til datapunktene, men jeg velger en eksponentiell modell, siden jeg mener at antall bensinbiler ikke vil "stupe" til 0, men heller bli gradvis færre, og flate ut på et lavt antall. Jeg velger en logistisk modell for antall elbiler, da den både passer godt til datapunktene, og kan være en modell som passer noen år frem i tid.
b)
Modellen for bensinbiler foreslår en nedgang i antall bensinbiler på 4 % årlig. Jeg mener modeller kan passe i flere år etter 2022, for eksempel frem til 2050, siden mange bytter ut bensinbilen sin med elbil. En gang i fremtiden kan det være at ingen lenger eier en bensinbil, men vi vet ikke når det eventuelt vil skje.
Modellen for elbiler kan passe i flere år etter 2022, f.eks. frem til 2030 eller 2040. Modellen viser at antall elbiler holder seg på samme antall fra ca. 2024. Det kan hende antall elbiler stabiliserer seg i Moss, men det kan også hende antallet fortsetter å øke (eller til og med synker!). Vi kan ikke vite det sikkert. Det kan komme færre fordeler og flere avgifter for elbiler - eller motsatt. Det er mye som spiller inn på hva slags bil folk velger.
Oppgave 6
a)
Lars prøver å finne ut størst mulig areal av det innskrevne rektangelet ABCD.
Svaret blir ca. 3,08 hvis man kjører programmet, som betyr at det største mulige arealet til rektangel ABCD er 3,08.
b)
Lars bruker definisjonen av den deriverte til å regne ut tilnærmet verdi av den deriverte i et punkt på funksjonen for areal av rektangelet (gitt i linje 4-5). Programmet gjør dette ved å regne ut stigningstallet i et veldig lite intervall (bredde 0,0001) på areal-funksjonen (linje 8-9).
Programmet starter med å beregne den deriverte i x=0. Så lenge den deriverte av areal-funksjonen er større enn 0, altså areal-funksjonen er voksende, fortsetter programmet å regne den deriverte i neste lille intervall (x øker med 0,01 for hver runde). Når den deriverte ikke lenger er større enn 0, vil man ha funnet en tilnærmet x-verdi for toppunktet. Programmet skriver til slutt ut y-verdien i toppunktet av areal-funksjonen, altså det største mulige arealet til ABCD.
Hvis målet er å finne toppunktet til en hvilken som helst funksjon, vil ikke strategien fungere dersom funksjonen ikke har noe toppunkt, og strategien vil heller ikke fungere hvis funksjonen er synkende fra x=0.
Oppgave 7
Pyramiden har størst volum dersom hjørnene i grunnflaten går helt ytterst til halvkulens overflate, og dersom høyden også går helt til halvkulens overflate.
Bruker CAS i Geogebra.
I linje 1 finner vi lengden på siden til grunnflaten. Svaret på linje 1 hadde endret seg da skjermbildet ble tatt, men det sto opprinnelig sammen uttrykk for s som defineres i linje 2.
I linje 3 beregnes arealet av grunnflaten.
I linje 4 defineres høyden h til å være lik radiusen r.
Volumet til den største mulige pyramiden er $V=\frac{2}{3}r^3$ (linje 5)