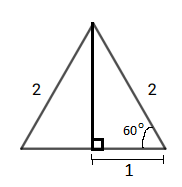1T 2023 høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (20 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[https://youtu.be/IkSMlCd8RP4 Videoløsning del 1 av Lektor Lainz] | |||
[https://youtu.be/rXLrV3wv0E0 Videoløsning del 2 av Lektor Lainz] | |||
=DEL 1= | =DEL 1= | ||
| Linje 80: | Linje 85: | ||
==Oppgave 4== | ==Oppgave 4== | ||
Jeg bruker arealsetningen for å beregne arealet til de to trekantene. | |||
Areal av trekanten til venstre: | |||
$A_1=\frac{1}{2}\cdot6\cdot6\cdot sin\,150^o=18 \cdot sin\,150^o$ | |||
Areal av trekanten til høyre: | |||
$A_2=\frac{1}{2}\cdot6\cdot6\cdot sin\,32^o=18 \cdot sin\,32^o$ | |||
Det som utgjør forskjellen i areal av de to trekantene, er sinusverdien til vinklene vi bruker i beregningen. | |||
[[File: 1T_H23_del1_oppg4.png|400px]] | |||
Jeg bruker enhetssirkelen, og ser at $sin\,32^o > sin\,150^o$. Derfor har trekanten til høyre størst areal. | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
$f(x)=\frac{2x-8}{x+2}$ | |||
Funksjonen f har lineær teller og nevner, og vil derfor ha en vannrett og en loddrett asymptote. Figur A, B eller C kan passe. | |||
Loddrett (vertikal) asymptote er i den x-verdien som gir null i nevner: | |||
$x+2 = 0\Rightarrow x=-2$ | |||
Vannrett (horisontal) asymptote: | |||
\[ y = \lim_{x\to \infty} \frac{2x-8}{x+2} = \lim_{x\to \infty} \frac{\frac{2x}{x}-\frac{8}{x}}{\frac{x}{x}+\frac{2}{x}} = \frac{2-0}{1+0} = 2 \] | |||
Figur C er den eneste figuren med loddrett asymptote på negativ side av x-aksen, og vannrett asymptote på positiv side av y-aksen. | |||
===b)=== | |||
$g(x)=\frac{x^2-4}{(x-3)(x+3)}$ | |||
Funksjonen g har to loddrette (vertikale) asymptoter, fordi det er to x-verdier som gir null i nevner, nemlig x = -3 og x = 3. De to asymptotene må være symmetriske om y-aksen. | |||
Funksjonen g har to nullpunkter, nemlig x = -2 og x = 2 (som gir null i teller, og derfor hele funksjonsverdien lik null). Disse er like langt fra origo i hver sin retning på x-aksen. | |||
Figur F er den eneste figuren med to loddrette asymptoter som er symmetriske om y-aksen, og to nullpunkter som også er symmetriske om y-aksen. | |||
=DEL 2= | =DEL 2= | ||
| Linje 141: | Linje 188: | ||
===b)=== | ===b)=== | ||
Jeg | Jeg viser her programmering i Python, hvor jeg kan angi antall linjestykker selv: | ||
[[File: 1T_H23_del2_7.png]] | [[File: 1T_H23_del2_7.png]] | ||
| Linje 187: | Linje 234: | ||
==Oppgave 5== | ==Oppgave 5== | ||
[[File: 1T_H23_del2_10.png]] | ===a)=== | ||
Bruker CAS i Geogebra. Finner f(1) og g(1), og differansen mellom disse to funksjonsverdiene. | |||
[[File: 1T_H23_del2_10.png|250px]] | |||
Avstanden fra P til Q er 6. | |||
===b)=== | |||
Lager en egen funksjon d(x) for differansen mellom f og g. Finner deretter ekstremalpunktene til d. Vi husker at a må være et tall mellom 1 og 3. Jeg sjekker grafisk at punktet jeg finner innenfor dette definisjonsområdet, er et toppunkt til d(x) (ikke vist her). | |||
[[File: 1T_H23_del2_11.png|450px]] | |||
Verdien til a som gir den største avstanden mellom R og S er $\frac{\sqrt{19}+1}{3}$ | |||
==Oppgave 6== | ==Oppgave 6== | ||
[[File: 1T_H23_del2_12.png]] | Bruker CAS i Geogebra. | ||
1. Definerer funksjonen | |||
2. Legger inn opplysning om toppunkt i (-8,0) – da er den deriverte lik 0 når x=-8 | |||
3. Legger inn opplysning om punktet (-8,0) – da er funksjonsverdien lik 0 når x=-8 | |||
4. Legger inn opplysning om gjennomsnittlig vekstfart – bruker formelen for gjennomsnittlig vekstfart. | |||
5. løser de tre foregående likningene. | |||
[[File: 1T_H23_del2_12.png|300px]] | |||
a, b og c har verdiene som vist i linje 5. | |||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 199: | Linje 267: | ||
===a)=== | ===a)=== | ||
[[File: 1T_H23_del2_13.png]] | Bruker CAS: | ||
[[File: 1T_H23_del2_13.png|200px]] | |||
Arealet av rektangelet regnes ut ved A=lengde*bredde. Lengden er 5, og bredden er f(5). | |||
Arealet av rektangelet er 8/9. | |||
===b)=== | ===b)=== | ||
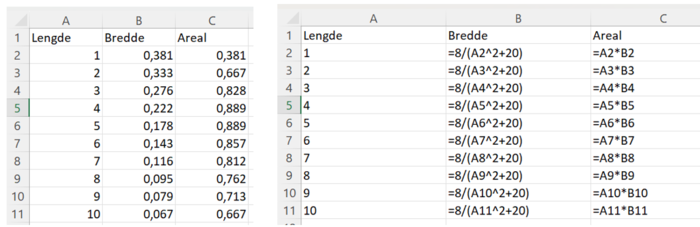
[[File: 1T_H23_del2_14.png]] | Bruker Excel: | ||
[[File: 1T_H23_del2_14.png|700px]] | |||
Det største arealet er når n=4 og n=5. | |||
===c)=== | ===c)=== | ||
[[File: 1T_H23_del2_15.png]] | Bruker CAS: | ||
[[File: 1T_H23_del2_15.png|300px]] | |||
1. definerer funksjonen f(x) | |||
2. definerer en funksjon for arealet av rektangelet, som en funksjon av k | |||
3. finner toppunktet til funksjonen for arealet av rektangelet, altså hvilken k som gir størst areal. Jeg sjekker grafisk at den positive verdien av k gir et toppunkt på A(k). (ikke vist her). | |||
k=4,472 gir størst areal av rektangelet. | |||
Siste sideversjon per 26. nov. 2024 kl. 08:38
Videoløsning del 1 av Lektor Lainz
Videoløsning del 2 av Lektor Lainz
DEL 1
Oppgave 1
Siden trekanten er likesidet, er alle vinklene like store. Hver vinkel er $180 : 3 = 60$ grader.
Jeg tegner inn høyden i trekanten, slik at jeg får en rettvinklet trekant, med hypotenus med lengde 2, og hosliggende katet til 60-gradersvinkelen med lengde 1 (se figur).
Jeg bruker definisjonen til cosinus av en vinkel i et rettvinklet trekant: cos v = hosliggende katet / hypotenus
Vi har at:
$cos \, 60^o = \frac{1}{2}$
Oppgave 2
Vi har $f(x)=x^3+2x^2-5x-6$
Siden f er en tredjegradsfunksjon, forventer jeg å finne opptil 3 nullpunkter. Jeg prøver meg frem med noen x-verdier, og finner at x = 2 er et nullpunkt, her vist ved regning:
$f(2)=2^3+2\cdot 2^2-5\cdot2-6=8+8-10-6=0$
Jeg utfører polynomdivisjonen f(x):(x-2) for å kunne finne de andre nullpunktene.
$\quad(x^3+2x^2-5x-6):(x-2)=x^2+4x+3$
$-(x^3-2x^2)$
$\quad \quad \quad 4x^2-5x-6$
$\quad\quad-(4x^2-8x)$
$\quad\quad\quad\quad\quad\quad3x-6$
$\quad\quad\quad\quad\quad-(3x-6)$
$\quad\quad\quad\quad\quad\quad\quad\quad0$
Jeg finner nullpunktene til andregradsuttrykket, ved å bruke abc-formelen:
$x^2+4x+3 = 0$
$x=\frac{-4\pm\sqrt{4^2-4\cdot1\cdot3}}{2\cdot 1}$
$x=\frac{-4\pm2}{2}$
$x_1=-3$ v $x_2=-1$
Nullpunktene til f(x) er x=-3, x=-1 og x=2, og det er i disse punktene grafen til funksjonen skjærer x-aksen.
Oppgave 3
$f(x)=x^3-3x^2-x+4$
For å finne likningen til tangenten i punktet $(1,f(1))$, vil jeg bruke ettpunktsformelen, $y-y_1=a(x-x_1)$
$x_1=1$, dette er x-koordinaten i punktet som er oppgitt.
Finner $y_1$:
$y_1=f(1)=1^3-3\cdot1^2-1+4=1$
For å finne a, må jeg finne f'(1).
$f'(x)=3x^2-6x-1$
$a=f'(1)=3-6-1=-4$
Setter inn i ettpunktsformelen:
$y-y_1=a(x-x_1)$
$y-1=-4(x-1)$
$y=-4x+5$
Likningen til tangenten til grafen til f i punktet $(1,f(1))$ er $y=-4x+5$.
Oppgave 4
Jeg bruker arealsetningen for å beregne arealet til de to trekantene.
Areal av trekanten til venstre:
$A_1=\frac{1}{2}\cdot6\cdot6\cdot sin\,150^o=18 \cdot sin\,150^o$
Areal av trekanten til høyre:
$A_2=\frac{1}{2}\cdot6\cdot6\cdot sin\,32^o=18 \cdot sin\,32^o$
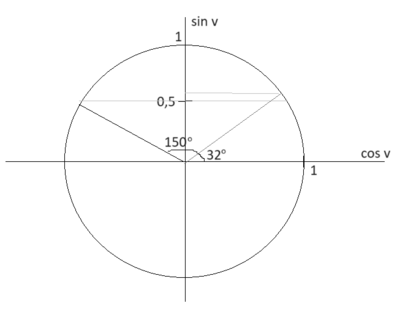
Det som utgjør forskjellen i areal av de to trekantene, er sinusverdien til vinklene vi bruker i beregningen.
Jeg bruker enhetssirkelen, og ser at $sin\,32^o > sin\,150^o$. Derfor har trekanten til høyre størst areal.
Oppgave 5
a)
$f(x)=\frac{2x-8}{x+2}$
Funksjonen f har lineær teller og nevner, og vil derfor ha en vannrett og en loddrett asymptote. Figur A, B eller C kan passe.
Loddrett (vertikal) asymptote er i den x-verdien som gir null i nevner:
$x+2 = 0\Rightarrow x=-2$
Vannrett (horisontal) asymptote:
\[ y = \lim_{x\to \infty} \frac{2x-8}{x+2} = \lim_{x\to \infty} \frac{\frac{2x}{x}-\frac{8}{x}}{\frac{x}{x}+\frac{2}{x}} = \frac{2-0}{1+0} = 2 \]
Figur C er den eneste figuren med loddrett asymptote på negativ side av x-aksen, og vannrett asymptote på positiv side av y-aksen.
b)
$g(x)=\frac{x^2-4}{(x-3)(x+3)}$
Funksjonen g har to loddrette (vertikale) asymptoter, fordi det er to x-verdier som gir null i nevner, nemlig x = -3 og x = 3. De to asymptotene må være symmetriske om y-aksen.
Funksjonen g har to nullpunkter, nemlig x = -2 og x = 2 (som gir null i teller, og derfor hele funksjonsverdien lik null). Disse er like langt fra origo i hver sin retning på x-aksen.
Figur F er den eneste figuren med to loddrette asymptoter som er symmetriske om y-aksen, og to nullpunkter som også er symmetriske om y-aksen.
DEL 2
Oppgave 1
a)
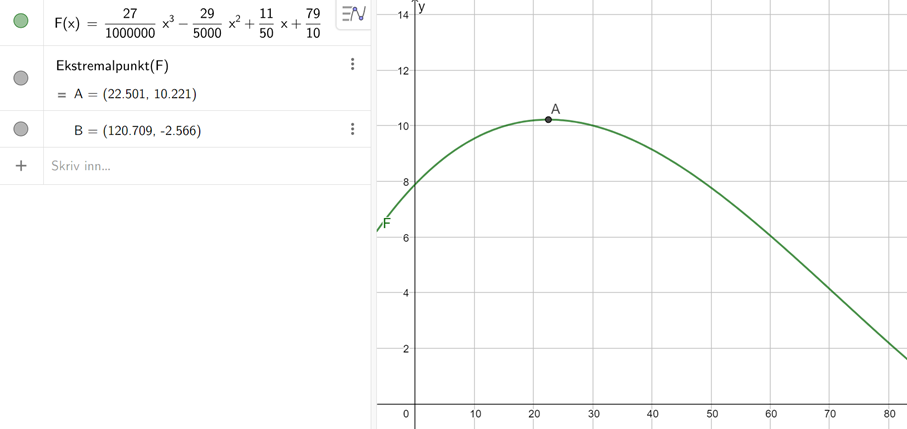
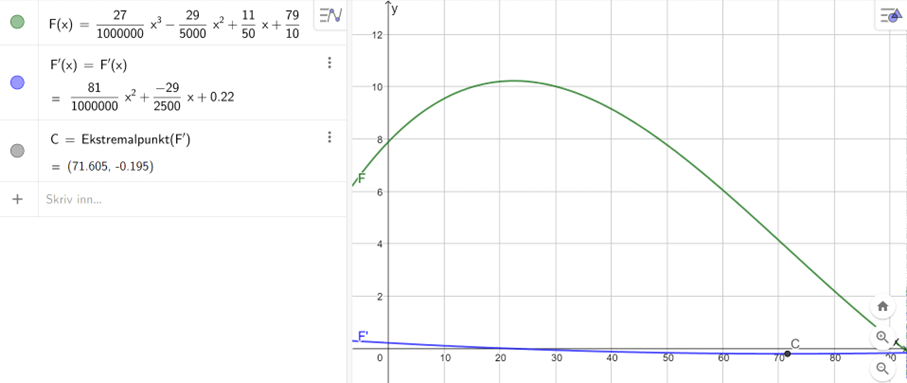
Metode 1: finne ekstremalpunktene ved å finne x-verdiene hvor den deriverte er lik 0. Det er kun én verdi innenfor definisjonsområdet. Sjekker om dette er et toppunkt, ved å sjekke at funksjonen vokser like før ekstremalpunktet, og synker like etter ekstremalpunktet.
Metode 2: Grafisk, ved å tegne grafen til F, og finne ekstremalpunktene. Det er da synlig at det er ett toppunkt i definisjonsområdet.
Høyeste folketall: 22.5 år etter 1960, altså i 1982.
b)
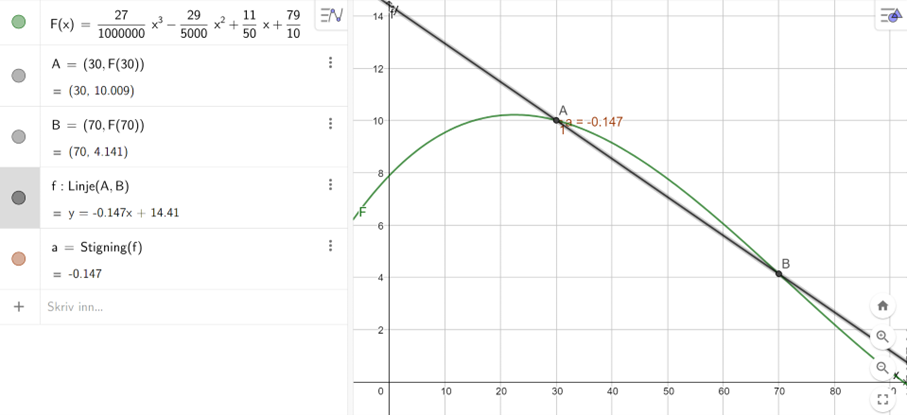
Tegner punktene A=(30,F(30)) og B=(70,F(70)) i Geogebra, tegner linjen som går gjennom punktene, og finner stigningen til linjen.
Stigningstallet er -0,147 tusen mennesker/år, som vil si at mellom 1990 og 2030, avtar folketallet gjennomsnittlig med 147 mennesker per år.
c)
Tegner grafen til F’(x), og finner bunnpunktet til denne (se punkt C).
Vi ser at F’ har lavest verdi for x=71.6, det vil si at folketallet avtar raskest i 2031.
Oppgave 2
1. Bruker cosinussetningen for å finne vinkel C.
2. Bruker arealsetningen for å finne arealet til trekant BCD.
3. Bruker sinussetningen for å finne lengden AB. Vinkel BDA er 180-125-35=20 grader.
4. Bruker arealsetningen for å finne arealet til trekan ABD.
5. Legger sammen arealet til trekantene, og finner arealet til ABCD.
Oppgave 3
a)
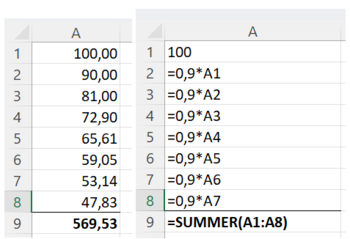
Bruker Excel til å finne lengden på de 8 første linjestykkene, og summerer deretter lengden på disse linjestykkene.
Summen av lengden av de 8 første linjestykkene er 569,5 cm.
b)
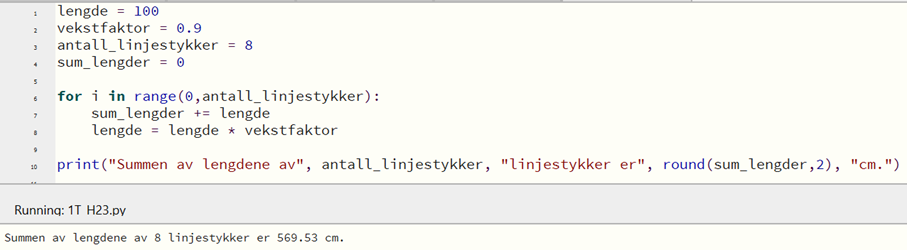
Jeg viser her programmering i Python, hvor jeg kan angi antall linjestykker selv:
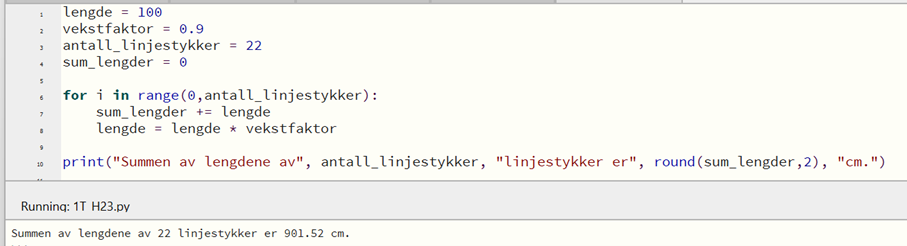
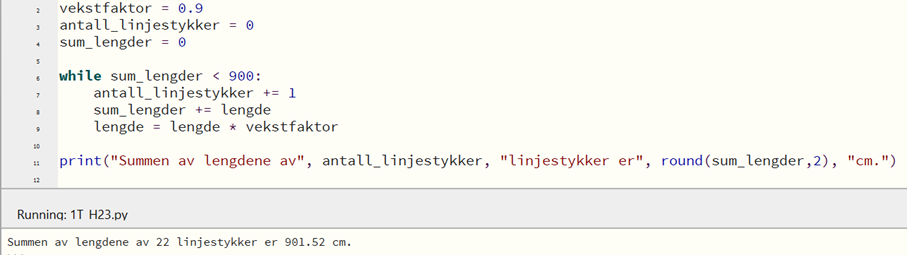
For å finne hvor mange linjestykker figuren må ha, for at summen av lengdene skal være minst 9 meter (900 cm), kan jeg prøve meg frem med antall linjestykker i programmet. Jeg finner at 22 linjestykker gir en sum på over 900 cm.
En bedre metode, hvor jeg ikke må prøve meg frem, er å bruke en while-løkke i stedet:
c)
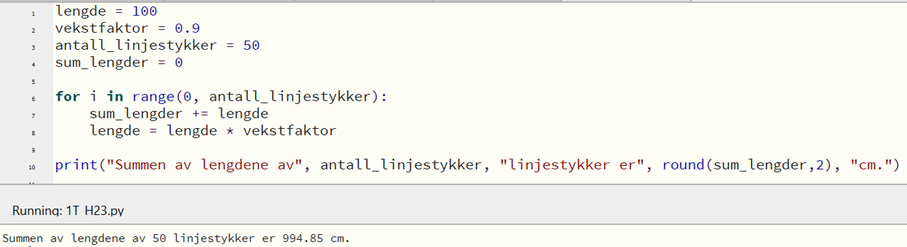
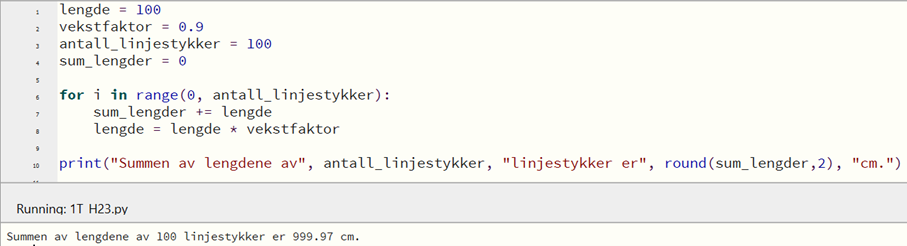
Bruker det første programmet mitt til å regne ut summen av lengdene til henholdsvis 50 og 100 linjestykker.
Regner ut hvor mange prosent forskjell det er for summen av lengdene:
$\frac{999,97 – 994,85}{994,85} \cdot 100 \% = 0,51 \% $
Det er ca. 0,51 % økning i summen av lengdene, dersom vi øker antall linjestykker i figuren fra 50 til 100.
Oppgave 4
a)
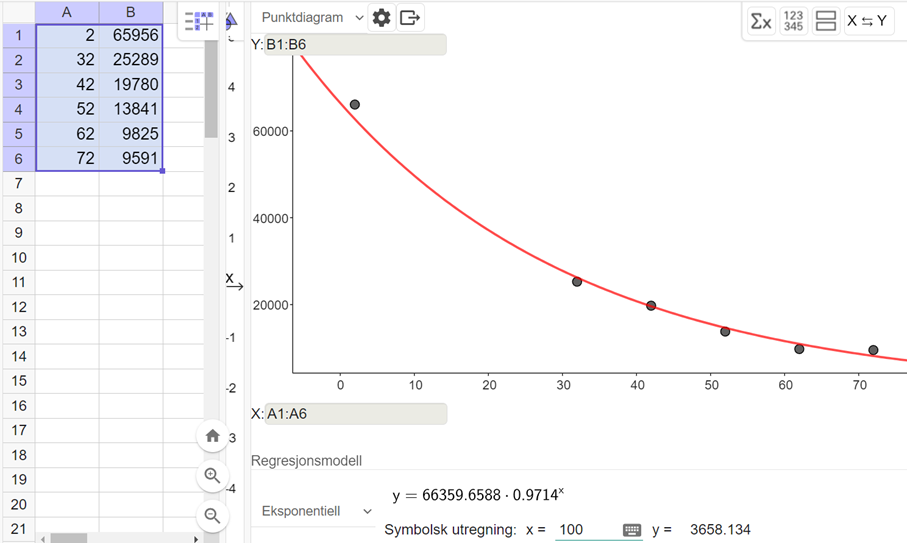
Utfører en regresjonsanalyse i Geogebra, og velger en eksponentiell modell, fordi den passer til punktene, og er typisk for en avtagende prosentvis vekst.
Modellen $F(x)=66360\cdot0.9714^x$
hvor x er antall år etter 1950, kan brukes til å si noe om antall personer som har hatt fiske som hovedyrke i perioden 1952-2022.
b)
Bruker "symbolsk utregning" i Geogebra (se oppgave a), hvor x= 100 gir en funksjonsverdi på ca. 3658 fiskere. Ifølge modellen vil det være ca. 3658 fiskere i 2050. Jeg antar at dette kan være et korrekt anslag, men vi kan ikke si det sikkert. Jeg vet lite om utviklingen av antall fiskere i Norge fremover, og det er mange faktorer som kan påvirke fremtidige yrkesvalg.
Modellens gyldighetsområde kan være for eksempel fra x = 0 til x = 100 (frem til 2050). Vi har bare målepunkter frem til 2022, men modellen kan muligens forutsi antall fiskere frem til 2050.
Oppgave 5
a)
Bruker CAS i Geogebra. Finner f(1) og g(1), og differansen mellom disse to funksjonsverdiene.
Avstanden fra P til Q er 6.
b)
Lager en egen funksjon d(x) for differansen mellom f og g. Finner deretter ekstremalpunktene til d. Vi husker at a må være et tall mellom 1 og 3. Jeg sjekker grafisk at punktet jeg finner innenfor dette definisjonsområdet, er et toppunkt til d(x) (ikke vist her).
Verdien til a som gir den største avstanden mellom R og S er $\frac{\sqrt{19}+1}{3}$
Oppgave 6
Bruker CAS i Geogebra. 1. Definerer funksjonen 2. Legger inn opplysning om toppunkt i (-8,0) – da er den deriverte lik 0 når x=-8 3. Legger inn opplysning om punktet (-8,0) – da er funksjonsverdien lik 0 når x=-8 4. Legger inn opplysning om gjennomsnittlig vekstfart – bruker formelen for gjennomsnittlig vekstfart. 5. løser de tre foregående likningene.
a, b og c har verdiene som vist i linje 5.
Oppgave 7
a)
Bruker CAS:
Arealet av rektangelet regnes ut ved A=lengde*bredde. Lengden er 5, og bredden er f(5).
Arealet av rektangelet er 8/9.
b)
Bruker Excel:
Det største arealet er når n=4 og n=5.
c)
Bruker CAS:
1. definerer funksjonen f(x) 2. definerer en funksjon for arealet av rektangelet, som en funksjon av k 3. finner toppunktet til funksjonen for arealet av rektangelet, altså hvilken k som gir størst areal. Jeg sjekker grafisk at den positive verdien av k gir et toppunkt på A(k). (ikke vist her).
k=4,472 gir størst areal av rektangelet.