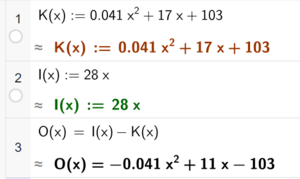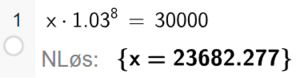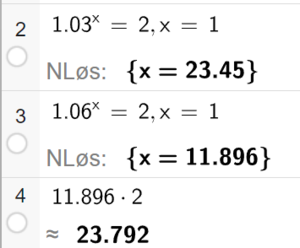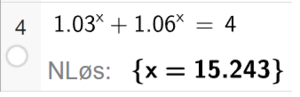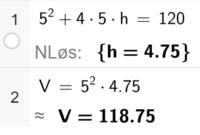S1 2023 Høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (67 mellomliggende versjoner av 6 brukere er ikke vist) | |||
| Linje 2: | Linje 2: | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=54561 Diskusjon av oppgaven på matteprat] | [https://matematikk.net/matteprat/viewtopic.php?f=13&t=54561 Diskusjon av oppgaven på matteprat] | ||
[https://lektorodd.github.io/lf/S1-H23/ Løysingsforslag laga av Torodd F. Ottestad] | |||
[https://matematikk.net/matteprat/download/file.php?id=4872 Løsningsforslag laget av Realfagsportalen] | |||
[https://matematikk.net/matteprat/download/file.php?id=4853 Løsningsforslag laget av Farhan Omar] | |||
[https://youtu.be/INZisk-GO30 Videoløsning del 1 av Lektor Lainz (Reabel)] | |||
==DEL 1== | |||
==Oppgave 1== | |||
$ {(\frac{3a^2}{2b^3})}^2 \cdot {( \frac{a^2b^{-5}}{4})}^{-1} = \frac{9 a^4 \cdot 4}{4b^6 \cdot a^2 \cdot b^{-5}} = \frac{9a^2}{b}$ | |||
==Oppgave 2== | |||
$2 \ln e^3 = 2\cdot 3 \ln e =6$ | |||
Vi vet at lg(70) er mellom 1 og 2 fordi lg(10) = 1 og lg(100) = 2. Derfor er 3lg(70) mellom 3 og 6 (større enn 3 og mindre enn 6). | |||
$e^{3\ln2} = e^{{\ln2}^3} = 2^3 = 8$ | |||
I stigende rekkefølge: | |||
$3 \lg(70), \quad 2 \ln e^3, \quad e^{3 \ln 2}$ | |||
==Oppgave 3== | |||
====a)==== | |||
P( alle terningen viser forskjellige øyner) = $\frac 66 \cdot \frac 56 \cdot \frac 46 =\frac{20}{36}=\frac{4\cdot 5}{4\cdot 9}= \frac 59$ | |||
====b)==== | |||
Sannsynligheten for at nøyaktig to terninger viser samme antall øyne, er alle muligheter minus sannnsynligheten for at alle terningene viser forskjellig antall øyne (funnet oppgave a), og minus sannsynligheten for at alle tre terningene viser samme antall øyne. | |||
Finner først sannsynligheten for at alle terningene viser samme antall øyne: P(alle like øyne) = $\frac 66 \cdot \frac 16 \cdot \frac 16 = \frac {1}{36}$ | |||
P(Kun to terninger viser det samme antall øyner) = $1 - P(alle \quad like) - P (alle \quad forskjellige) = \frac{36}{36}- \frac{1}{36} - \frac{20}{36} = \frac {15}{36} = \frac {5}{12}$ | |||
==Oppgave 4== | |||
<math>f(x)= \bigg{\lbrace} \begin{array}{cc} | |||
x^2+ 3x - a^2, & x < 1 \\ | |||
x-1, & x\geq 1 \\ | |||
\end{array} | |||
</math> | |||
$f(1)= 1-1 = 0$ | |||
$\lim\limits_{x \to 1^-} f(x) = \lim\limits_{ x \to 1^-} (x^2 + 3x - a^2) = 4-a^2$ | |||
For at funksjonen skal være kontinuerlig må funksjonsverdien bli null når x går mot en nedenfra. Dvs. $a = \pm 2$ | |||
==Oppgave 5== | |||
Programmet finner hvor mange enheter som må produseres for at grensekostnaden skal bli lik 200 kroner. Det vil si det antallet enheter som må produseres, for at det skal koste 200 kr å produsere én til. | |||
$K(x) = 0,1x^2+100x+9000$ | |||
$K'(x)=0,2x+100$ | |||
Setter K'(x)=200 | |||
$0,2x+100=200$ | |||
$x=\frac{100}{0,2}=\frac{1000}{2}=500$ | |||
Resultatet er at det må produseres 500 enheter for at grensekostnaden skal være 200 kroner. | |||
=DEL 2= | |||
==Oppgave 1== | |||
===a)=== | |||
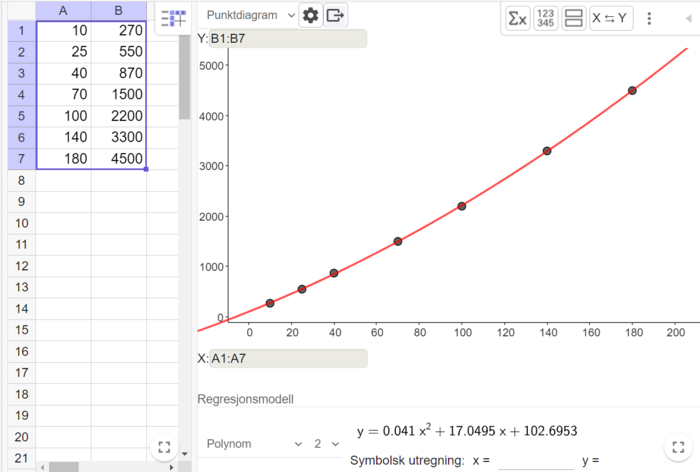
Bruker regresjonsanalyse i Geogebra til å finne et andregradsuttrykk for produksjonskostnaden. | |||
[[File: S1_H23_del2_1a1.png |700px]] | |||
Bruker CAS til å definere kostnadsfunksjonen K(x) (fra regresjonsanalysen), inntektsfunksjonen I(x) (i tusen kroner), og til slutt overskuddsfunksjonen O(x). O(x) er slik det skulle vises. | |||
[[File: S1_H23_del2_1a2.png|300px]] | |||
===b)=== | |||
Bruker CAS til å finne toppunktet i overskuddsfunksjonen. Oppgaven kan også løses grafisk. | |||
[[File: S1_H23_del2_1b.png|200px]] | |||
En produksjon på 134 sofaer gir størst overskudd per måned. | |||
===c)=== | |||
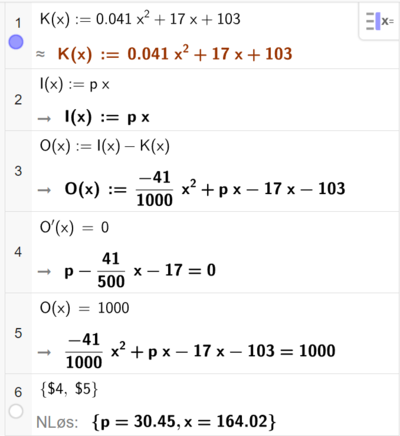
Løser oppgaven i CAS. Oppgaven kan også løses grafisk, med glider for prisen p. | |||
[[File: S1_H23_del2_1c.png|400px]] | |||
For å nå et overskudd på 1 million kroner per måned, må prisen settes opp til 30 450 kr per sofa. Da må det også produseres 164 sofaer. | |||
==Oppgave 2== | |||
===a)=== | |||
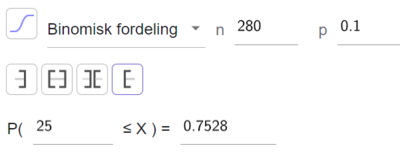
Jeg bruker sannsynlighetskalkulatoren i Geogebra og velger binomisk fordeling. | |||
[[File: S1_H23_del2_2a.png|400px]] | |||
m sannsynligheten for at minst 25 av guttene på skolen er venstrehendte er ca. 75 %. | |||
===b)=== | |||
Jeg prøver meg frem og endrer n i sannsynlighetskalkulatoren. | |||
[[File: S1_H23_del2_2b.png|400px]] | |||
Det må være minst 16 gutter i klassen for at sannsynligheten for at minst tre av guttene er venstrehendte, skal være større enn 20 prosent. | |||
===c)=== | |||
Bruker sannsynlighetskalkulatoren til Geogebra på samme måte som over, og finner verdiene jeg trenger. | |||
$P(G=3) \cdot P(J=0) + P(G=2) \cdot P(J=1) + P(G=1) \cdot P(J=2) + P(G=0) \cdot P(J=3)$ | |||
$ = 0,0997 \cdot 0,2423 + 0,2448 \cdot 0,3582 + 0,3672 \cdot 0,2498 + 0,2442 \cdot 0,1083$ | |||
$= 0,23 $ | |||
Det er 23 % sannsynlighet for at nøyaktig tre av elevene i klassen er venstrehendte. | |||
==Oppgave 3== | |||
===a)=== | |||
Bruker CAS i Geogebra. | |||
[[File: S1_H23_del2_3a.png|300px]] | |||
Per må sette inn ca. 23 682,3 kr på konto, for å ha 30 000 kr på konto etter 8 år. | |||
===b)=== | |||
[[File: S1_H23_del2_3b.png|300px]] | |||
Med 3 % rente tar det 23,45 år å doble beløpet, mens det med 6 % rente tar 11,896 år å doble beløpet. 11,896 ganget med to er ikke nøyaktig likt 23,45 år, og derfor er påstanden feil. | |||
===c)=== | |||
[[File: S1_H23_del2_3c.png|300px]] | |||
Det tar 15,24 år før Per og Kåre til sammen har dobbelt så mye | |||
penger som de satte inn på kontoene. | |||
Hvorfor = 4 i likningen? Forklaring: | |||
Per setter inn et beløp b. Kåre setter inn samme beløp b. Til sammen har de allerede beløpet 2b. Skal dette doble seg, må vi få 4b. Beløpets størrelse har ingen betydning. Vi kunne like gjerne skrive likningen $b\cdot 1.03^x+b\cdot 1.06^x=4\cdot b$, og forkorte alle b'ene. | |||
==Oppgave 4== | |||
===a)=== | |||
P(minst to terninger med samme antall øyne) = 1 - P(alle terningene viser ulikt antall øyne) = $1-\frac 66 \frac 56 \frac 46 \frac 36 \frac 26 = 1 - \frac{5}{54} = \frac{49}{54}\approx 0,907$ | |||
Sannsynligheten for at minst to av terningene viser samme antall | |||
øyne er 90,7 %. | |||
===b)=== | |||
Jeg programmerer i Python. | |||
[[File: S1_H23_del2_4b2.png|600px]] | |||
Sannsynligheten for å for en sum på mer enn 20 øyne, i et kast med 5 terninger, er ca. 22 %. | |||
===c)=== | |||
Jeg prøver meg frem og endrer verdien i linje 11. | |||
[[File: S1_H23_del2_4c.png|600px]] | |||
Den største verdien er $k$ som er slik at $P(X\geq k)>0,8$ er 14. | |||
==Oppgave 5== | |||
===a)=== | |||
Bruker CAS i Geogebra. | |||
[[File: S1_H23_del2_5a.png|200px]] | |||
Linje 1: overfaltearealet skal være 120 kvadratdesimeter. Regner ut hva høyden må være når sidene i bunnen er 5 dm. | |||
Linje 2: regner ut volumet når sidene i bunnen er 5 dm og høyden er 4,75. | |||
Det største volumet kassen kan få dersom sidene i bunnen skal være | |||
5 dm er 118,75 kubikkdesimeter. | |||
===b)=== | |||
[[File: S1_H23_del2_5b.png|700px]] | |||
Det maksimale volumet kassen kan få er ca. 126,5 kubikkdesimeter. | |||
===c)=== | |||
[[File: S1_H23_del2_5c.png|700px]] | |||
det minste samlede arealet platene kan ha, for en kasse som rommet 80 kubikkdesimeter, er ca. 88,4 kvadratdesimeter. | |||
==Oppgave 6== | |||
===a)=== | |||
Påstanden er usann. Grafen til f har ikke nødvendigvis noe ekstremalpunkt. For eksempel har $f(x)=x^3$ ingen ekstremalpunkter. | |||
===b)=== | |||
Påstanden er sann. Alle slike linjer har $D_f=\mathbb{R}$ og $V_f=\mathbb{R}$ , slik også en tredjegradsfunksjon har. Funksjonene må derfor skjære hverandre. | |||
===c)=== | |||
[[File: S1_H23_del2_6c.png|300px]] | |||
Påstanden er sann. | |||
Siste sideversjon per 11. jul. 2024 kl. 10:23
Diskusjon av oppgaven på matteprat
Løysingsforslag laga av Torodd F. Ottestad
Løsningsforslag laget av Realfagsportalen
Løsningsforslag laget av Farhan Omar
Videoløsning del 1 av Lektor Lainz (Reabel)
DEL 1
Oppgave 1
$ {(\frac{3a^2}{2b^3})}^2 \cdot {( \frac{a^2b^{-5}}{4})}^{-1} = \frac{9 a^4 \cdot 4}{4b^6 \cdot a^2 \cdot b^{-5}} = \frac{9a^2}{b}$
Oppgave 2
$2 \ln e^3 = 2\cdot 3 \ln e =6$
Vi vet at lg(70) er mellom 1 og 2 fordi lg(10) = 1 og lg(100) = 2. Derfor er 3lg(70) mellom 3 og 6 (større enn 3 og mindre enn 6).
$e^{3\ln2} = e^{{\ln2}^3} = 2^3 = 8$
I stigende rekkefølge:
$3 \lg(70), \quad 2 \ln e^3, \quad e^{3 \ln 2}$
Oppgave 3
a)
P( alle terningen viser forskjellige øyner) = $\frac 66 \cdot \frac 56 \cdot \frac 46 =\frac{20}{36}=\frac{4\cdot 5}{4\cdot 9}= \frac 59$
b)
Sannsynligheten for at nøyaktig to terninger viser samme antall øyne, er alle muligheter minus sannnsynligheten for at alle terningene viser forskjellig antall øyne (funnet oppgave a), og minus sannsynligheten for at alle tre terningene viser samme antall øyne.
Finner først sannsynligheten for at alle terningene viser samme antall øyne: P(alle like øyne) = $\frac 66 \cdot \frac 16 \cdot \frac 16 = \frac {1}{36}$
P(Kun to terninger viser det samme antall øyner) = $1 - P(alle \quad like) - P (alle \quad forskjellige) = \frac{36}{36}- \frac{1}{36} - \frac{20}{36} = \frac {15}{36} = \frac {5}{12}$
Oppgave 4
<math>f(x)= \bigg{\lbrace} \begin{array}{cc} x^2+ 3x - a^2, & x < 1 \\ x-1, & x\geq 1 \\ \end{array} </math>
$f(1)= 1-1 = 0$
$\lim\limits_{x \to 1^-} f(x) = \lim\limits_{ x \to 1^-} (x^2 + 3x - a^2) = 4-a^2$
For at funksjonen skal være kontinuerlig må funksjonsverdien bli null når x går mot en nedenfra. Dvs. $a = \pm 2$
Oppgave 5
Programmet finner hvor mange enheter som må produseres for at grensekostnaden skal bli lik 200 kroner. Det vil si det antallet enheter som må produseres, for at det skal koste 200 kr å produsere én til.
$K(x) = 0,1x^2+100x+9000$
$K'(x)=0,2x+100$
Setter K'(x)=200
$0,2x+100=200$
$x=\frac{100}{0,2}=\frac{1000}{2}=500$
Resultatet er at det må produseres 500 enheter for at grensekostnaden skal være 200 kroner.
DEL 2
Oppgave 1
a)
Bruker regresjonsanalyse i Geogebra til å finne et andregradsuttrykk for produksjonskostnaden.
Bruker CAS til å definere kostnadsfunksjonen K(x) (fra regresjonsanalysen), inntektsfunksjonen I(x) (i tusen kroner), og til slutt overskuddsfunksjonen O(x). O(x) er slik det skulle vises.
b)
Bruker CAS til å finne toppunktet i overskuddsfunksjonen. Oppgaven kan også løses grafisk.
En produksjon på 134 sofaer gir størst overskudd per måned.
c)
Løser oppgaven i CAS. Oppgaven kan også løses grafisk, med glider for prisen p.
For å nå et overskudd på 1 million kroner per måned, må prisen settes opp til 30 450 kr per sofa. Da må det også produseres 164 sofaer.
Oppgave 2
a)
Jeg bruker sannsynlighetskalkulatoren i Geogebra og velger binomisk fordeling.
m sannsynligheten for at minst 25 av guttene på skolen er venstrehendte er ca. 75 %.
b)
Jeg prøver meg frem og endrer n i sannsynlighetskalkulatoren.
Det må være minst 16 gutter i klassen for at sannsynligheten for at minst tre av guttene er venstrehendte, skal være større enn 20 prosent.
c)
Bruker sannsynlighetskalkulatoren til Geogebra på samme måte som over, og finner verdiene jeg trenger.
$P(G=3) \cdot P(J=0) + P(G=2) \cdot P(J=1) + P(G=1) \cdot P(J=2) + P(G=0) \cdot P(J=3)$
$ = 0,0997 \cdot 0,2423 + 0,2448 \cdot 0,3582 + 0,3672 \cdot 0,2498 + 0,2442 \cdot 0,1083$
$= 0,23 $
Det er 23 % sannsynlighet for at nøyaktig tre av elevene i klassen er venstrehendte.
Oppgave 3
a)
Bruker CAS i Geogebra.
Per må sette inn ca. 23 682,3 kr på konto, for å ha 30 000 kr på konto etter 8 år.
b)
Med 3 % rente tar det 23,45 år å doble beløpet, mens det med 6 % rente tar 11,896 år å doble beløpet. 11,896 ganget med to er ikke nøyaktig likt 23,45 år, og derfor er påstanden feil.
c)
Det tar 15,24 år før Per og Kåre til sammen har dobbelt så mye penger som de satte inn på kontoene.
Hvorfor = 4 i likningen? Forklaring:
Per setter inn et beløp b. Kåre setter inn samme beløp b. Til sammen har de allerede beløpet 2b. Skal dette doble seg, må vi få 4b. Beløpets størrelse har ingen betydning. Vi kunne like gjerne skrive likningen $b\cdot 1.03^x+b\cdot 1.06^x=4\cdot b$, og forkorte alle b'ene.
Oppgave 4
a)
P(minst to terninger med samme antall øyne) = 1 - P(alle terningene viser ulikt antall øyne) = $1-\frac 66 \frac 56 \frac 46 \frac 36 \frac 26 = 1 - \frac{5}{54} = \frac{49}{54}\approx 0,907$
Sannsynligheten for at minst to av terningene viser samme antall øyne er 90,7 %.
b)
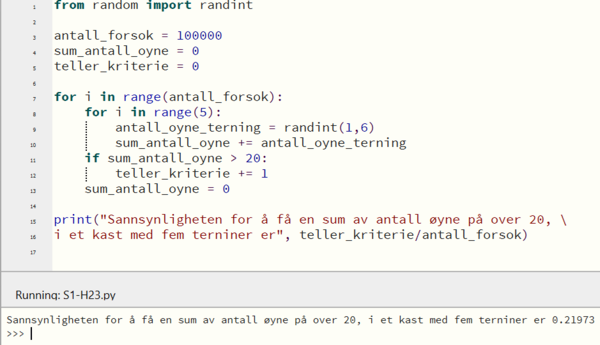
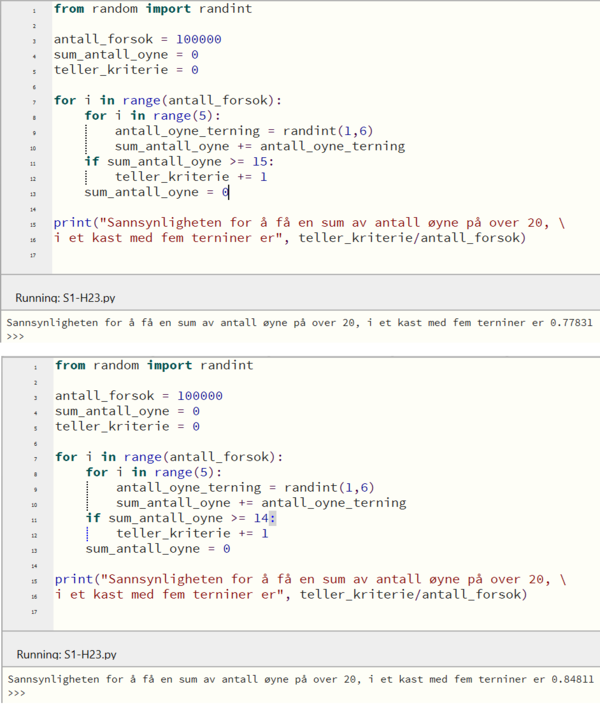
Jeg programmerer i Python.
Sannsynligheten for å for en sum på mer enn 20 øyne, i et kast med 5 terninger, er ca. 22 %.
c)
Jeg prøver meg frem og endrer verdien i linje 11.
Den største verdien er $k$ som er slik at $P(X\geq k)>0,8$ er 14.
Oppgave 5
a)
Bruker CAS i Geogebra.
Linje 1: overfaltearealet skal være 120 kvadratdesimeter. Regner ut hva høyden må være når sidene i bunnen er 5 dm.
Linje 2: regner ut volumet når sidene i bunnen er 5 dm og høyden er 4,75.
Det største volumet kassen kan få dersom sidene i bunnen skal være 5 dm er 118,75 kubikkdesimeter.
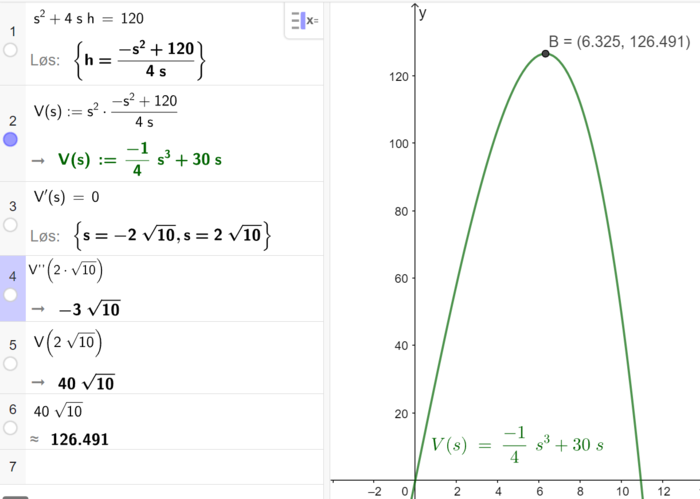
b)
Det maksimale volumet kassen kan få er ca. 126,5 kubikkdesimeter.
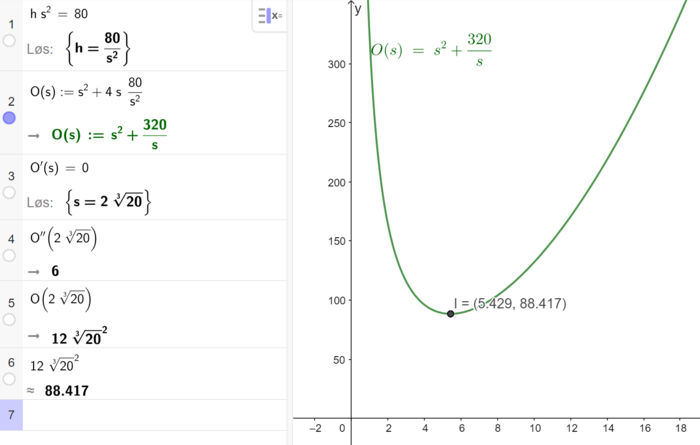
c)
det minste samlede arealet platene kan ha, for en kasse som rommet 80 kubikkdesimeter, er ca. 88,4 kvadratdesimeter.
Oppgave 6
a)
Påstanden er usann. Grafen til f har ikke nødvendigvis noe ekstremalpunkt. For eksempel har $f(x)=x^3$ ingen ekstremalpunkter.
b)
Påstanden er sann. Alle slike linjer har $D_f=\mathbb{R}$ og $V_f=\mathbb{R}$ , slik også en tredjegradsfunksjon har. Funksjonene må derfor skjære hverandre.
c)
Påstanden er sann.