Løsning del 2 utrinn Vår 23: Forskjell mellom sideversjoner
Lagt til enda en videoløsning for Del 2 |
|||
| (15 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 3: | Linje 3: | ||
[https://matematikk.net/matteprat/viewtopic.php?f=1&t=54322 Diskusjon av denne oppgaven på matteprat] | [https://matematikk.net/matteprat/viewtopic.php?f=1&t=54322 Diskusjon av denne oppgaven på matteprat] | ||
[https://youtu.be/Ha9nTw4Hzik?si=53VsEPMzYvW_m1jf Videoløsning av Del 2 av Sander Syvertsen] | |||
[https://youtu.be/JA96323xPYY Videoløsning av Lektor Lainz (Reabel matte)] | |||
==DEL TO== | ==DEL TO== | ||
| Linje 76: | Linje 79: | ||
===Oppgave 7=== | ===Oppgave 7=== | ||
Fra veiledningen: | |||
''I oppgave 7 og 8 presenterer vi en situasjon eller en | |||
''problemstilling der du selv skal undersøke og utforske. | |||
''I disse oppgavene vil vi se etter din kompetanse i å: | |||
''• vurdere hva du vil utforske og formulere matematiske | |||
''spørsmål knyttet til innhold i oppgaven | |||
''• vise fremgangsmåte/resonnement og besvare de | |||
''matematiske spørsmålene du formulerer | |||
''• bruke hensiktsmessige hjelpemiddel | |||
''• argumentere for løsningene dine og gjøre kritiske | |||
''vurderinger | |||
''Vi anbefaler å bruke omtrent 60 minutter på oppgave 7 og 8 til | |||
''sammen. | |||
'''Boble 1''' | '''Boble 1''' | ||
| Linje 91: | Linje 114: | ||
'''Boble 4''' | '''Boble 4''' | ||
Vi finner en generell løsning for arealet av det blå området: dersom man tar første kvadratsetning minus andre kvadratsetning, der a og b har samme verdi i begge ($a \neq b$) får man: | |||
$(a+b)(a+b) - (a-b)(a-b) = a^2+2ab+ b^2 -(a^2 -2ab +b^2)= 2ab + 2ab = 4ab $ | $(a+b)(a+b) - (a-b)(a-b) = a^2+2ab+ b^2 -(a^2 -2ab +b^2)= 2ab + 2ab = 4ab $ | ||
| Linje 97: | Linje 120: | ||
===Oppgave 8=== | ===Oppgave 8=== | ||
Jeg begynner med å gjøre beregninger basert på informasjonen i boblene (og tabellen): | |||
'''Bilen har et årlig verditap på 10%:''' | |||
Etter to år er bilens verdi: $83600\cdot 0,9^2=67716$ kr. | |||
Det samlede verdifallet i løpet av to år er $83600-67716 = 15884 $ kr, som tilsvarer et tap på ca. 15884/ 24 = 662 kr per måned. | |||
'' | '''Drivstoffkostnader:''' | ||
'' | |||
'' | |||
Med et forbruk på 0,3 liter/ mil og en ukentlig kjørelengde på 6,5 mil blir det et forbruk på 0,3*6,5 = 1,95 liter i uken, eller ca 1,95*4 = 7,8 liter i måneden. Dersom bensinprisen er 21kr per liter, blir det en månedlig kostnad på 7,8*21 = 163,8 = ca. 164 kroner. Bensinprisen er utenfor Thereses kontroll og kan godt stige. | |||
Fordi det månedlige forbruket er lavt, utgjør drivstoffutgiftene ca. en fjerdedel av bilens månedlige verditap (164/662 = ca. 1/4) | |||
''' Sparepenger''' | |||
Sparepengene har stått på konto i 3 år med 1,5 % årlig rente. Det betyr at hun for 3 år siden satte inn: | |||
$41827\cdot 1,015^{-3}=40000$ kroner på konto. | |||
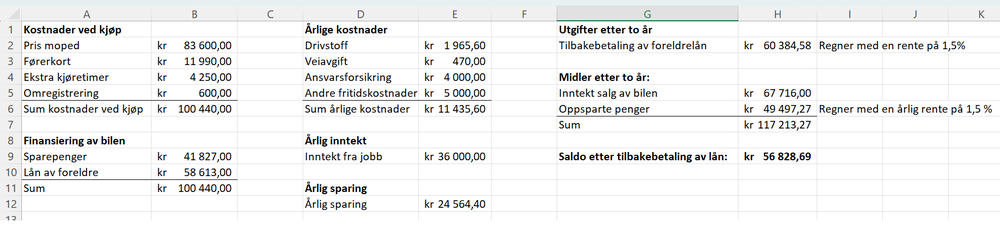
Therese bør sette opp et budsjett. Det blir dyrt for henne å betale både førerkort og prisen på bilen, så jeg foreslår at hun låner penger fra foreldrene. Etter to år vil hun ha tjent nok gjennom jobben til å både betale kostnader knyttet til bilen, og annen fritid. Hun an også betale lånet tilbake, og ha penger til overs. | |||
, | |||
[[File: usk-v23-del2-8.png | 1000px]] | |||
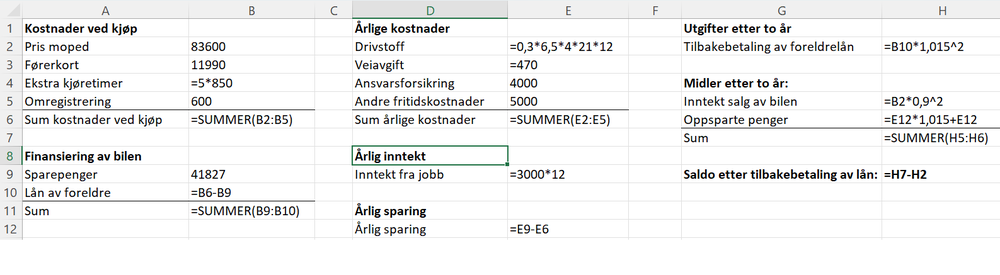
[[File: usk-v23-del2-8-formler.png |1000px]] | |||
Siste sideversjon per 18. mai 2024 kl. 14:02
Diskusjon av denne oppgaven på matteprat
Videoløsning av Del 2 av Sander Syvertsen
Videoløsning av Lektor Lainz (Reabel matte)
DEL TO
Oppgave 1
Flex er billigst dersom du leier for mer enn 100 minutter. For kortere tid er Wheele billigst.
Leien for Flex er kr. 100 pluss kr. 2 per minutt.
Leien for Wheele er kr. 50 pluss kr. 2,50 per minutt.
Oppgave 2
Her kan man tenke brøk: Antallet man betaler for setter man i teller. Antallet man får setter man i nevner. Man ønsker da brøken så liten som mulig fordi man ønsker å få mange, men betale for så få som mulig. Tilbud 1: $\frac 35$
Tilbud 2: 25% er det samme som at du betaler for 3 og får den 4., altså $\frac 34$
Tilbud 3: Tilbudet er det samme som i 2.
Tilbud 4: $\frac 23$
I tilbud 1 betaler man for 60% av varene (6/10). Det er best. I tilbud 2 og 3 betaler man for 75% og i tilbud 4 betaler man for 67% av varene.
Oppgave 3
a)
Det var 30 elever med på undersøkelsen. De fikk tilsammen 2700 kroner i ukepenger. Det gir et gjennomsnitt på 90 kroner per person.
b)
Det kan vi ikke si noe om. Dersom en elev var borte har denne 400 kroner i lommepenger, fordi (2700 + 400):31 =100. Dersom 100 elever var borte hadde disse 103 kr i gjennomsnitt i lommepenger. Ut fra de opplysningene kan man ikke si noe om hvor mange det er på 10. trinn. x
Oppgave 4
Arealet av en sirkel er gitt som $A = \pi r^2$
Dersom man skal finne arealet av en halvsirkel kan man halvere $r^2$ og ikke r. Halvors løsning er derfor feil.
Kvadratet av 6 er 36 og kvadratet av 3 er 9, men 9 er ikke halvparten av 36, selv om 3 er halvparten av 6.
Oppgave 5
a)
Den blå blokken er en løkke som gjentar seg så mange ganger som den verdien du gir inn i det grå feltet: "antall_terningkast". Inne i løkken skjer to ting. Det trekkes et tilfeldig tall fra og med en til og med seks. Det trukkede tallet legges til i en liste. Når løkken er ferdig skrives listen til skjermen.
b)
Sannsynlighet er relativ frekvens i det lange løp. Det betyr at man må ha mange terningkast. Dersom vi velger et veldig stort tall vil datamaskinen jobbe lenge for å kjøre programmet. Det er ikke ønskelig. Jeg ville prøvd med tre forskjellige verdier. 100, 1000 og 10000. Jo større tallet er jo nærmere kommer de forskjellige utfallene 16,7%.
Oppgave 6
Det er mest lønnsomme å velge kronen som dobler seg 14 ganger:
1, 2,4,8,16,32,......
er det samme som
$2^0, 2^1, 2^2, 2^3, 2^4, 2^5, ...$
$2^{14}= 16384$
Oppgave 7
Fra veiledningen:
I oppgave 7 og 8 presenterer vi en situasjon eller en problemstilling der du selv skal undersøke og utforske. I disse oppgavene vil vi se etter din kompetanse i å:
• vurdere hva du vil utforske og formulere matematiske spørsmål knyttet til innhold i oppgaven
• vise fremgangsmåte/resonnement og besvare de matematiske spørsmålene du formulerer
• bruke hensiktsmessige hjelpemiddel
• argumentere for løsningene dine og gjøre kritiske vurderinger
Vi anbefaler å bruke omtrent 60 minutter på oppgave 7 og 8 til sammen.
Boble 1
Utsagnet stemmer fordi 4+2 er 6 og 6 kvadrert er 36.
Boble 2
4 minus 2, ganger 4 minus 2, er to ganger to som er 4, så arealet av det blå området er ganske riktig 36- 4 = 32.
Boble 3
Samme tanke som over gir 20, som også er i samsvar med generell løsning nedenfor.
Boble 4
Vi finner en generell løsning for arealet av det blå området: dersom man tar første kvadratsetning minus andre kvadratsetning, der a og b har samme verdi i begge ($a \neq b$) får man:
$(a+b)(a+b) - (a-b)(a-b) = a^2+2ab+ b^2 -(a^2 -2ab +b^2)= 2ab + 2ab = 4ab $
Oppgave 8
Jeg begynner med å gjøre beregninger basert på informasjonen i boblene (og tabellen):
Bilen har et årlig verditap på 10%:
Etter to år er bilens verdi: $83600\cdot 0,9^2=67716$ kr.
Det samlede verdifallet i løpet av to år er $83600-67716 = 15884 $ kr, som tilsvarer et tap på ca. 15884/ 24 = 662 kr per måned.
Drivstoffkostnader:
Med et forbruk på 0,3 liter/ mil og en ukentlig kjørelengde på 6,5 mil blir det et forbruk på 0,3*6,5 = 1,95 liter i uken, eller ca 1,95*4 = 7,8 liter i måneden. Dersom bensinprisen er 21kr per liter, blir det en månedlig kostnad på 7,8*21 = 163,8 = ca. 164 kroner. Bensinprisen er utenfor Thereses kontroll og kan godt stige.
Fordi det månedlige forbruket er lavt, utgjør drivstoffutgiftene ca. en fjerdedel av bilens månedlige verditap (164/662 = ca. 1/4)
Sparepenger
Sparepengene har stått på konto i 3 år med 1,5 % årlig rente. Det betyr at hun for 3 år siden satte inn:
$41827\cdot 1,015^{-3}=40000$ kroner på konto.
Therese bør sette opp et budsjett. Det blir dyrt for henne å betale både førerkort og prisen på bilen, så jeg foreslår at hun låner penger fra foreldrene. Etter to år vil hun ha tjent nok gjennom jobben til å både betale kostnader knyttet til bilen, og annen fritid. Hun an også betale lånet tilbake, og ha penger til overs.