2P 2022 Høst eksempel LK20 LØSNING: Forskjell mellom sideversjoner
| (19 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 49: | Linje 49: | ||
==Oppgave 4== | ==Oppgave 4== | ||
[[File: 2P-H22-del1-4.png| | [[File: 2P-H22-del1-4.png|600px]] | ||
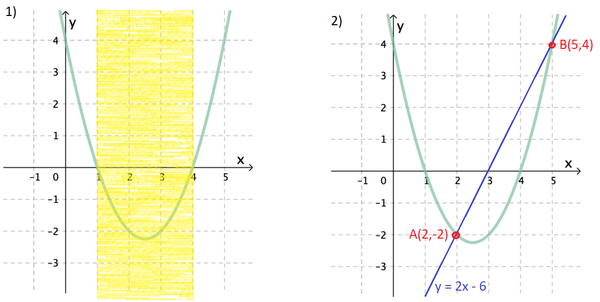
1) Ulikheten $x^2-5x < -4$ tilsvarer ulikheten $x^2-5x+4<0$. Vi kan se på grafen til $f$, og finne ut at funksjonsverdien er mindre enn null, for x-verdier mellom 1 og 4 (markert med gult på figuren til venstre). Løsningen på ulikheten er $1<x<4$. | 1) Ulikheten $x^2-5x < -4$ tilsvarer ulikheten $x^2-5x+4<0$. Vi kan se på grafen til $f$, og finne ut at funksjonsverdien er mindre enn null, for x-verdier mellom 1 og 4 (markert med gult på figuren til venstre). Løsningen på ulikheten er $1<x<4$. | ||
| Linje 99: | Linje 99: | ||
Beholder C ser ut som beholder B, bare snudd på hodet. Derfor tenker jeg at første del av beholder C fylles med samme hastighet som siste del av beholder B, og omvendt. Det tar like lang tid å fylle begge beholderne. | Beholder C ser ut som beholder B, bare snudd på hodet. Derfor tenker jeg at første del av beholder C fylles med samme hastighet som siste del av beholder B, og omvendt. Det tar like lang tid å fylle begge beholderne. | ||
[[File: 2P-H22-del2-5b.png]] | [[File: 2P-H22-del2-5b.png|300px]] | ||
==Oppgave 6== | ==Oppgave 6== | ||
| Linje 109: | Linje 109: | ||
===b)=== | ===b)=== | ||
[[File: 2P-H22-del2-6b.png| | [[File: 2P-H22-del2-6b.png|500px]] | ||
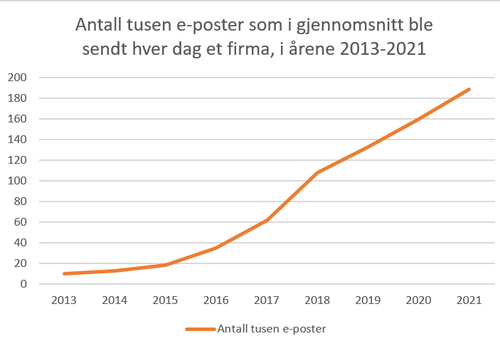
Diagrammet er mindre misvisende fordi alle årstall er med på x-aksen. Man ser bedre at det ikke var så høy vekst i antall eposter sendt per dag i årene 2018-2021, som det kunne se ut som i det første diagrammet. Jeg har imidlertid valgt noen sannsynlige funksjonsverdier i årene 2014, 2019, og 2020t, så jeg kan ikke vite helt sikkert at det stemmer med virkeligheten. | Diagrammet er mindre misvisende fordi alle årstall er med på x-aksen. Man ser bedre at det ikke var så høy vekst i antall eposter sendt per dag i årene 2018-2021, som det kunne se ut som i det første diagrammet. Jeg har imidlertid valgt noen sannsynlige funksjonsverdier i årene 2014, 2019, og 2020t, så jeg kan ikke vite helt sikkert at det stemmer med virkeligheten. | ||
| Linje 118: | Linje 118: | ||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | |||
$\angle BEA$ og $\angle DEC$ er toppvinkler, og er derfor like store. | |||
Siden AB og CD er parallelle, og $\angle EAB$ og $\angle ECD$ deler et vinkelbein, er disse samsvarende vinkler, og er derfor like store. | |||
To trekanter er formlike hvis de har parvis like store vinkler, hvilket er vist. | |||
===b)=== | |||
Areal til $\Delta ABE$: | |||
$A=\frac{g\cdot h}{2}=\frac{5\cdot 8}{2}=20$ | |||
Bruker formlikhet til å finne høyden til $\Delta CDE$: | |||
$\frac{h}{CD}=\frac{h_2}{AB}$ | |||
$\frac{h}{20}=\frac{5}{8}$ | |||
$h=\frac{5}{8}\cdot 20$ | |||
$h= 12,5$ | |||
Areal til $\Delta CDE$: | |||
$A=\frac{g\cdot h}{2}=\frac{20\cdot 12,5}{2}=125$ | |||
Totalt areal = areal_ABE + areal_CDE = 20 + 125 = 145 kvadratmeter. | |||
==Oppgave 8== | ==Oppgave 8== | ||
===a)=== | |||
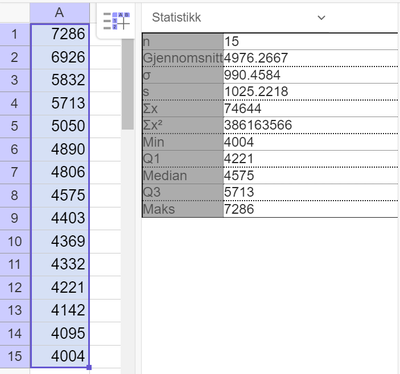
Legger inn tallene i regnearket i Geogebra, bruker "analyse av en variabel", og "vis statistikk". | |||
[[File: 2P-H22-del2-8.png|400px]] | |||
Gjennomsnitt: 4976 hytter | |||
Median: 4575 hytter | |||
Standardavvik: 1025 hytter (velger s og ikke sigma, siden dette er en stikkprøve fra en større populasjon). | |||
===b)=== | |||
1) Ingrid vil få et lavere gjennomsnittlig antall hytter, siden den første lista var lista over de 15 stedene med flest hytter/fritidsbygg i Norge. Da vil sted nr. 16-30 selvfølgelig ha færre hytter/fritidsboliger, enn sted nr. 1-15 på lista. | |||
2) Det er ikke mulig å avgjøre om det vil være større forskjell mellom median og gjennomsnitt. For eksempel kan sted nr. 16 ha 4000 hytter, mens sted nr. 17-30 kan ha 200 hytter. Da vil det være stor forskjell på median og gjennomsnitt. Eller så kan f.eks. sted 16-30 alle ha rundt 3500 hytter, og da vil det var liten forskjell mellom median og gjennomsnitt. | |||
3) Det er ikke mulig å avgjøre om hun vil få et høyere eller lavere standardavvik. Det kommer an på om antall hytter i noen av stedene nr. 16-30 spriker veldig fra gjennomsnittet, eller ikke. | |||
==Oppgave 9== | ==Oppgave 9== | ||
En økning på 250 % gir en vekstfaktor på 3,5. Utregning: $1+\frac{250}{100}=1+2,5=3,5$ | |||
Ny verdi = gammel verdi * vekstfaktor $\iff$ Gammel verdi = ny verdi / vekstfaktor | |||
Gammel verdi = $\frac{15\,000\,000}{3,5} \approx 4\,285\,714$ | |||
Omtrent 4,3 millioner personer reiste til og fra norske flyplasser i samme periode i 2021. | |||
==Oppgave 10== | ==Oppgave 10== | ||
===a)=== | |||
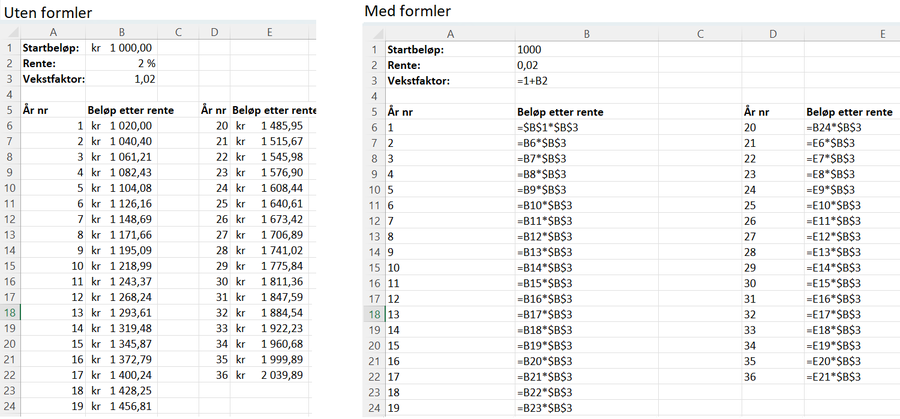
Med regneark: | |||
[[File: 2P-h22-del2-10.png|900px]] | |||
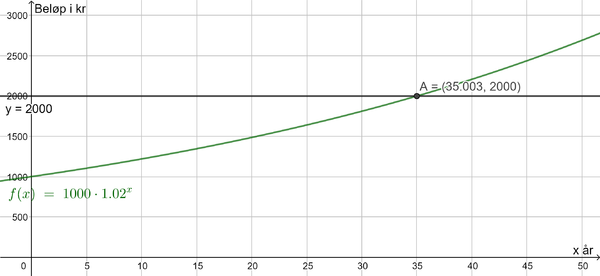
Grafisk: | |||
[[File: 2P-h22-del2-10b.png|600px]] | |||
Begge metoder gir det samme svaret; beløpet (her 1000 kr) er nesten doblet etter 35 år (eller mer enn doblet etter 36 år). | |||
===b)=== | |||
Bruker CAS i Geogebra til å sammenligne. | |||
Kolonne 1 viser en likning som finner antall år det tar å doble et beløp, med ulike rentesatser, hhv. 1 %, 2 %, 3 %, 4 %, 5 %, 25 %, og 50 %. | |||
Kolonne 2 viser "72-regelen" for de samme rentesatsene. Det ser ut som om 72-regelen stemmer nogenlunde. | |||
[[File: 2P-H22-del2-10bc.png|400px]] | |||
===c)=== | |||
Kolonne 3 i bildet over viser "70-regelen". Det ser ut som 70-regelen stemmer bedre for lave rentesatser, men 72-regelen passer bedre for svært høye rentesatser. Vanligvis er renter på sparing nokså lave (for tiden rundt 2-3 %), slik at 70-regelen er fornuftig å bruke. | |||
Siste sideversjon per 27. des. 2022 kl. 14:10
Diskusjon av oppgaven på matteprat
Løsningsforslag som pdf laget av Farhan Omar
DEL 1
Oppgave 1
a)
Median: sorterer tallene i stigende rekkefølge, og tar gjennomsnittet av de to midterste tallene.
15 15 15 20 20 20 25 25 25 100
Begge de to midterste tallene er 20, så medianen er 20.
Gjennomsnitt:
$\frac{15\cdot3 + 20\cdot 3 + 25 \cdot 3 + 100}{10} = \frac{45 + 60 + 75 + 100}{10} = \frac{280}{10} = 28$
b)
I 9 av de 10 dagene leste Maia 15, 20 eller 25 sider. Sånn sett beskriver medianen datamaterialet best.
Den ene dagen hun leste 100 sider var et unntak, og det høye tallet gjør at gjennomsnittet er litt høyt i forhold til antall sider hun leste de fleste dagene.
Oppgave 2
2015: KPI på 100 og lønn på 400 000 kr.
2019: KPI på 110,8 og lønn på 440 000 kr.
Det er flere måter å tenke på for å løse oppgaven. Spørsmålet er om lønnen har gått opp mer enn konsumprisindeksen, eller ikke.
Konsumprisindeksen har gått fra 100 til 110,8, altså opp 10,8 %. Har lønnen gått opp mer eller mindre enn 10,8 %?
Lønnen har gått fra 400 000 kr til 440 000 kr, altså har lønnen gått opp med 40 000 kr. Det er akkurat 10 % av 400 000 kr.
Oppsummert: KPI har gått opp 10,8 %, men lønnen har bare gått opp 10 %. Det betyr at Anna faktisk hadde størst kjøpekraft i 2015.
Oppgave 3
If-setningen i programmet sjekker om Pytagoras-setningen stemmer for en trekant med sider a, b og c. Programmet kan brukes til å sjekke om trekanten er rettvinklet eller ikke.
En passende tekst i print-funksjonen i linje 11 er: "Trekanten er rettvinklet".
Oppgave 4
1) Ulikheten $x^2-5x < -4$ tilsvarer ulikheten $x^2-5x+4<0$. Vi kan se på grafen til $f$, og finne ut at funksjonsverdien er mindre enn null, for x-verdier mellom 1 og 4 (markert med gult på figuren til venstre). Løsningen på ulikheten er $1<x<4$.
2) For å løse likningen $x^2 −5x + 4 = 2x −6$, kan vi tegne inn linja $y=2x-6$ i samme koordinatsystem, og se hvor grafene til funksjonene har lik funksjonsverdi. Dette skjer i punkt A og B (markert med rødt på figuren til høyre). Løsningene på likningen er $x=2 \vee x=5$.
DEL 2
Oppgave 1
Finner et punkt på hver graf, hvor x- og y-verdien er lettleselig.
Graf A: velger punktet (10, 220). Det betyr at 10 hg kaffe koster 220 kr. Det gir en pris på 22 kr per hektogram.
Graf B: velger punktet (10, 80). Det betyr at 10 hg kaffe koster 80 kr. Det gir en pris på 8 kr per hektogram.
Prisforskjellen er altså $22-8=14$ kr per hektogram.
Oppgave 2
Mellom -28 og 56 er det 7a. Differansen mellom 56 og -28 er 84. Utregning: $56-(-28)=84$.
Hver a er verdt 12. Utregning: $\frac{84}{7}=12$.
Da er 2a verdt 24. Utregning: $2\cdot 12 = 24$.
I ruta skal det stå -4. Utregning: $-28+24 = -4$
Oppgave 3
Dersom 1,5 % tilsvarer 300 kr, har vi at 1 % tilsvarer 200 kr.
Da vil 4 % tilsvare 800 kr. Prisøkningen ville vært på 800 kr.
Oppgave 4
Det er diagram E som viser sammenhengen mellom lengden (x) og bredden (y) i hvert rektangel. Det er en omvendt proporsjonal sammenheng, hvor $y=\frac{A}{x}$ (fordi $A = x\cdot y$).
Oppgave 5
a)
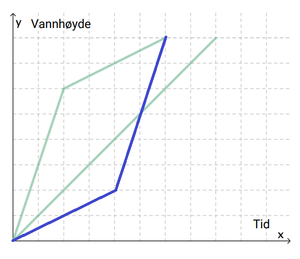
Den rette linja er grafen som viser sammenhengen mellom tid og vannhøyde for beholder A. Hele beholderen har samme diameter, og vannhøyden vil derfor øke med konstant fart (lineær vekst).
Den grafen som består av to rette linjer med ulik vekstfart, er den som viser sammenhengen mellom tid og vannhøyde for beholder B. Dette er fordi vannhøyden først øker raskt der hvor beholderen har liten diameter, og deretter øker saktere der hvor beholderen har større diameter.
b)
Beholder C ser ut som beholder B, bare snudd på hodet. Derfor tenker jeg at første del av beholder C fylles med samme hastighet som siste del av beholder B, og omvendt. Det tar like lang tid å fylle begge beholderne.
Oppgave 6
a)
Diagrammet er misvisende, fordi det ikke er like mange antall år mellom hvert merke (med lik avstand) på x-aksen.
b)
Diagrammet er mindre misvisende fordi alle årstall er med på x-aksen. Man ser bedre at det ikke var så høy vekst i antall eposter sendt per dag i årene 2018-2021, som det kunne se ut som i det første diagrammet. Jeg har imidlertid valgt noen sannsynlige funksjonsverdier i årene 2014, 2019, og 2020t, så jeg kan ikke vite helt sikkert at det stemmer med virkeligheten.
c)
Det kan se ut som Jens sin påstand stemmer. På den justerte diagrammet i oppgave b), ser det ut som det er raskest vekst i antall eposter som i gjennomsnitt ble sendt hver dag, mellom 2017 og 2018. Vi vet imidlertid ikke helt sikkert hvordan veksten har vært mellom 2018 og 2019, 2019 og 2020, og 2020-2021. Det kan godt hende at ett av årene hadde en kjempehøy vekst i antall eposter sendt per dag.
Oppgave 7
a)
$\angle BEA$ og $\angle DEC$ er toppvinkler, og er derfor like store.
Siden AB og CD er parallelle, og $\angle EAB$ og $\angle ECD$ deler et vinkelbein, er disse samsvarende vinkler, og er derfor like store.
To trekanter er formlike hvis de har parvis like store vinkler, hvilket er vist.
b)
Areal til $\Delta ABE$:
$A=\frac{g\cdot h}{2}=\frac{5\cdot 8}{2}=20$
Bruker formlikhet til å finne høyden til $\Delta CDE$:
$\frac{h}{CD}=\frac{h_2}{AB}$
$\frac{h}{20}=\frac{5}{8}$
$h=\frac{5}{8}\cdot 20$
$h= 12,5$
Areal til $\Delta CDE$:
$A=\frac{g\cdot h}{2}=\frac{20\cdot 12,5}{2}=125$
Totalt areal = areal_ABE + areal_CDE = 20 + 125 = 145 kvadratmeter.
Oppgave 8
a)
Legger inn tallene i regnearket i Geogebra, bruker "analyse av en variabel", og "vis statistikk".
Gjennomsnitt: 4976 hytter
Median: 4575 hytter
Standardavvik: 1025 hytter (velger s og ikke sigma, siden dette er en stikkprøve fra en større populasjon).
b)
1) Ingrid vil få et lavere gjennomsnittlig antall hytter, siden den første lista var lista over de 15 stedene med flest hytter/fritidsbygg i Norge. Da vil sted nr. 16-30 selvfølgelig ha færre hytter/fritidsboliger, enn sted nr. 1-15 på lista.
2) Det er ikke mulig å avgjøre om det vil være større forskjell mellom median og gjennomsnitt. For eksempel kan sted nr. 16 ha 4000 hytter, mens sted nr. 17-30 kan ha 200 hytter. Da vil det være stor forskjell på median og gjennomsnitt. Eller så kan f.eks. sted 16-30 alle ha rundt 3500 hytter, og da vil det var liten forskjell mellom median og gjennomsnitt.
3) Det er ikke mulig å avgjøre om hun vil få et høyere eller lavere standardavvik. Det kommer an på om antall hytter i noen av stedene nr. 16-30 spriker veldig fra gjennomsnittet, eller ikke.
Oppgave 9
En økning på 250 % gir en vekstfaktor på 3,5. Utregning: $1+\frac{250}{100}=1+2,5=3,5$
Ny verdi = gammel verdi * vekstfaktor $\iff$ Gammel verdi = ny verdi / vekstfaktor
Gammel verdi = $\frac{15\,000\,000}{3,5} \approx 4\,285\,714$
Omtrent 4,3 millioner personer reiste til og fra norske flyplasser i samme periode i 2021.
Oppgave 10
a)
Med regneark:
Grafisk:
Begge metoder gir det samme svaret; beløpet (her 1000 kr) er nesten doblet etter 35 år (eller mer enn doblet etter 36 år).
b)
Bruker CAS i Geogebra til å sammenligne.
Kolonne 1 viser en likning som finner antall år det tar å doble et beløp, med ulike rentesatser, hhv. 1 %, 2 %, 3 %, 4 %, 5 %, 25 %, og 50 %.
Kolonne 2 viser "72-regelen" for de samme rentesatsene. Det ser ut som om 72-regelen stemmer nogenlunde.
c)
Kolonne 3 i bildet over viser "70-regelen". Det ser ut som 70-regelen stemmer bedre for lave rentesatser, men 72-regelen passer bedre for svært høye rentesatser. Vanligvis er renter på sparing nokså lave (for tiden rundt 2-3 %), slik at 70-regelen er fornuftig å bruke.