S1 2022 Høst LK20 LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
mIngen redigeringsforklaring |
||
| (55 mellomliggende versjoner av 4 brukere er ikke vist) | |||
| Linje 3: | Linje 3: | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=54141 Diskusjon av denne oppgaven på matteprat] | [https://matematikk.net/matteprat/viewtopic.php?f=13&t=54141 Diskusjon av denne oppgaven på matteprat] | ||
[https://matematikk.net/matteprat/download/file.php?id=4563 Løsning laget av Farhan Omar] | |||
[https://lektorodd.github.io/lf/S1-H22/ Løysing laga av Torodd F. Ottestad] | |||
===Oppgave 2=== | =DEL EN= | ||
==Oppgave 1== | |||
$(2a^{-2} b)^{-1} \cdot ({\frac{b^2}{a}})^2 =$ $\frac{a^2}{2b} \cdot \frac{b^4}{a^2}= \frac{b^3}{2} $ | |||
==Oppgave 2== | |||
===a)=== | ===a)=== | ||
$ O(x)= -0.05x^2+100x-10000$ | |||
$O'(x) = -0,10x+100$ | |||
$O'(500)= -50 +100 =50$ | |||
Den momentane veksten ved 500 produserte enheter er 50 kr. Det betyr at dersom produksjonen øker med en enhet vil overskuddet øke med 50 kr. | |||
===b)=== | ===b)=== | ||
===Oppgave 3=== | Overskuddsfunksjonen er en parabel som vender sin hule side ned. Den har da et maksimum for O'(x) = 0: | ||
$-0.10x + 100 = 0$ | |||
$x=1000$ | |||
O(1000) = 40 000 kroner. | |||
==Oppgave 3== | |||
$\lg(x+3)+\lg x =1$ | |||
$\lg((x+3)x) =1$ | |||
= | $10^{\lg(x^2+3x)} = 10^1$ | ||
$x^2-3x-10 =0$ | |||
$x=5$ | |||
(kun positiv løsn. pga log) | |||
==Oppgave 4== | |||
$\lim\limits_{h \to 0} \frac{(4+h)^2-4^2}{h}$ | |||
Dette ser i utgangspunktet ut som et null over null utrykk. Vi får rydde litt: | |||
$\lim\limits_{h \to 0} \frac{(16+8h+ h^2)-16}{h} = \lim\limits_{h \to 0} \frac{h(8+ h)}{h} =8 $ | |||
==Oppgave 5== | |||
===a)=== | |||
Dersom ikke begge kulene er sorte er minst en hvit. | |||
P(minst en hvit) = 1 - P(to sorte) = 1 - $\frac{6}{8} \cdot \frac{5}{7} = \frac{13}{28}$ | |||
===b)=== | |||
antall hvite kuler (h) = 2 | |||
antall svarte kuler (s) = 0 | |||
sannsynligheten (P) for å trekke 2 svarte kuler = 0 | |||
Så lenge (while) sannsynligheten er mindre enn 0,5: | |||
- legge til 1 svart kule (s=s+1) | |||
- $P=\frac{s}{h+s}\cdot\frac{s-1}{h+s-1}$ | |||
- når løkken er ferdig: skrive ut verdien for antall svarte kuler, og sannsynligheten for å trekke to svarte kuler. | |||
=DEL TO= | |||
==Oppgave 1== | |||
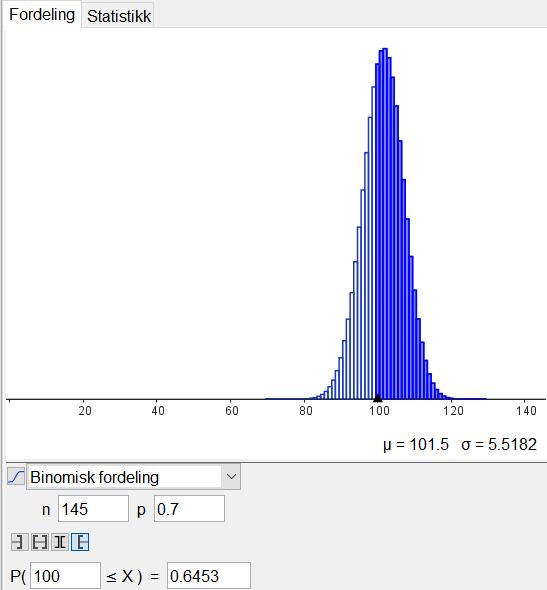
Dette kan oppfattes som en binomisk situasjon | |||
*Om hendelsen inntreffer eller ikke: turist eller ikke. | |||
*Vi regner sannsynligheten som lik i alle delforsøk, fordi det er mange turister. | |||
*Delforsøkene er uavhengige. (Dette er neppe helt riktig) | |||
[[File:311222-01.png]] | |||
Det er ca. 65% sannsynlig. | |||
==Oppgave 2== | |||
===a)=== | |||
[[File:301222-01.png]] | |||
Definerer x | |||
*Finer tangenten g(x) i et vilkårlig punkt a | |||
*Finner tangentens skjæringer med aksene | |||
*Finner uttrykket for arealet | |||
Arealet av trekanten blir ca. 0,78 (linje 6) når koordinatene til P er $( \frac 12, \frac 34)$ | |||
===b)=== | |||
Vi deriverer arealfunksjonen og setter den lik null, løser likningen. Se linje 8 og 9 i del a. Minste areal ca. 0,77. | |||
==Oppgave 3== | |||
===a)=== | |||
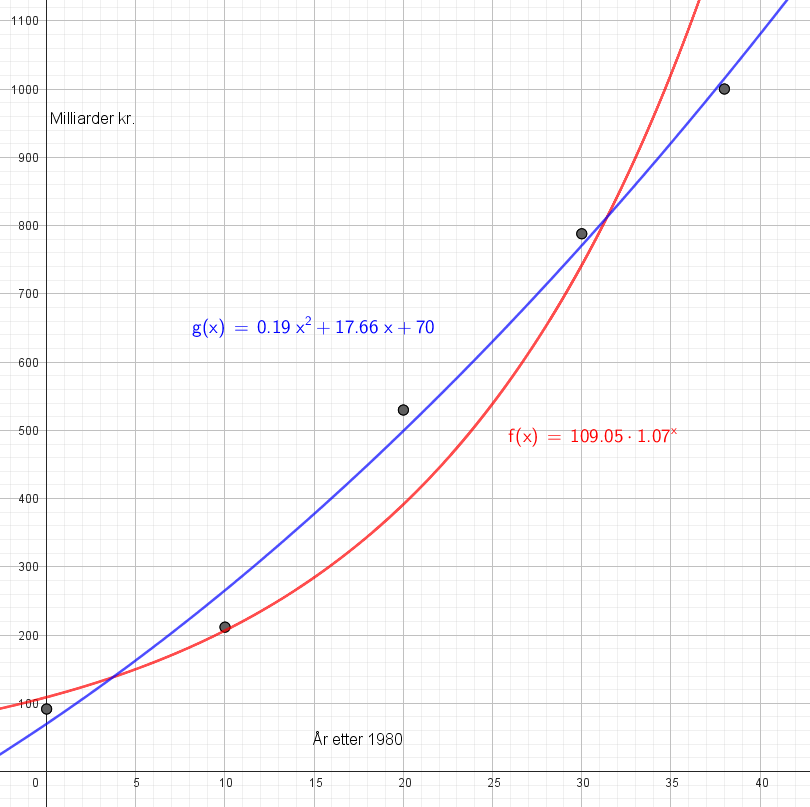
[[File:171122-2.png]] | |||
Å basere en "modell" på historiske data og forvente at den skal gi et bilde av fremtiden er omtrent som å tro på julenissen. For å si noe om framtiden trenger vi informasjon og forutsetninger utover historiske data. | |||
Begge grafene gir et bilde av det som har vært. Polynomfunksjonen gir best sammenheng med en kvadrert regresjonskoeffisient på 0,9917. Begge funksjoner vokser med en takt som neppe er bærekraftig. Polynomfunksjonen vokser minst og vil trolig ligge nærmest den framtidige virkelighet, selv om oppgaven mangler informasjon til å kunne si noe fornuftig om det. | |||
===b)=== | |||
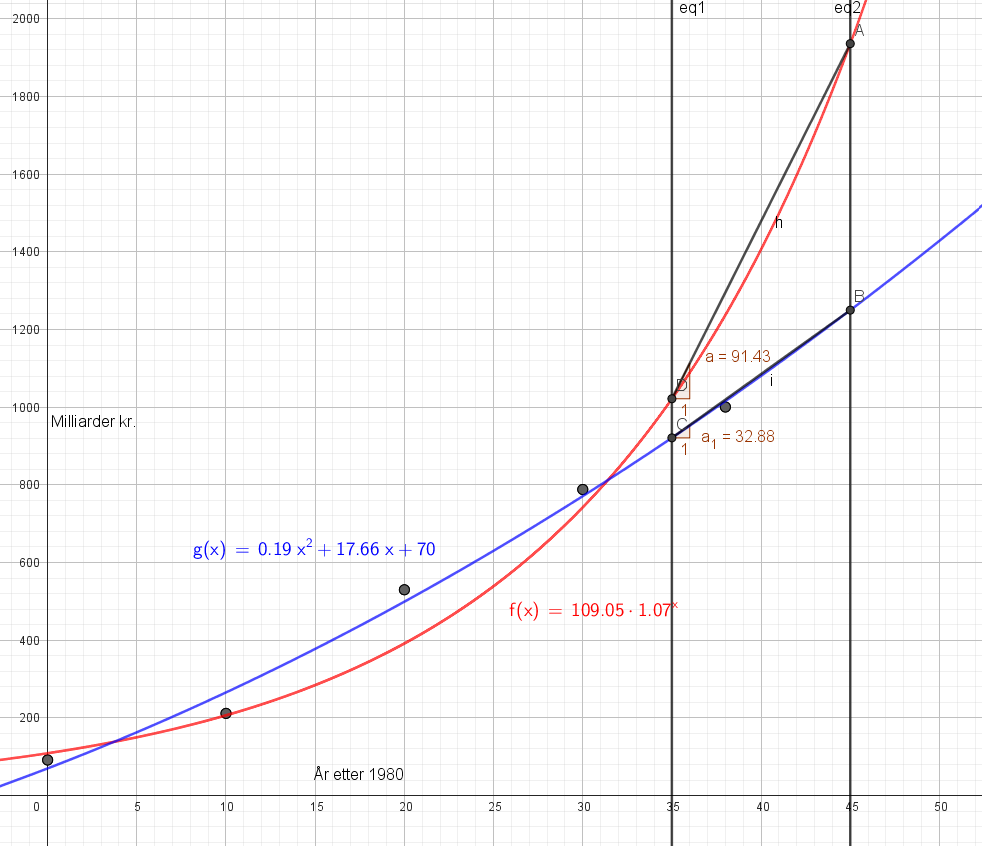
[[File:171122-3.png]] | |||
Veksten er 33 og 91 milliarder per å i gjennomsnitt for henholdsvis g og f. | |||
===c)=== | |||
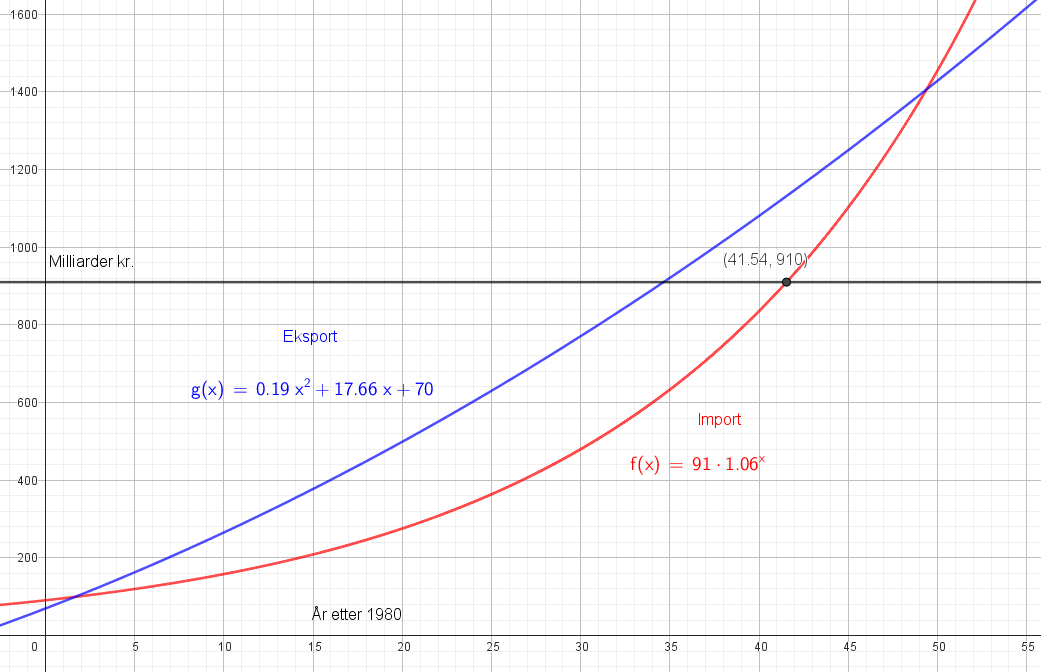
[[File:171122-5.png]] | |||
===d)=== | |||
==Oppgave 4== | |||
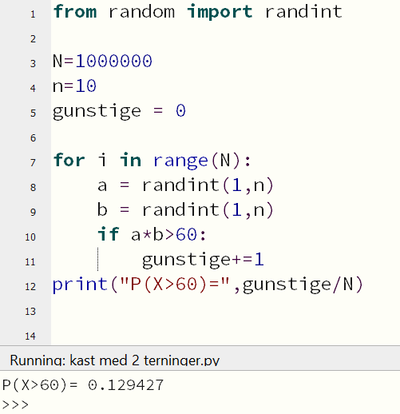
===a)=== | |||
[[File: S1-H22-del2-6a.png|400px]] | |||
$P(X>60)\approx 0,13$ | |||
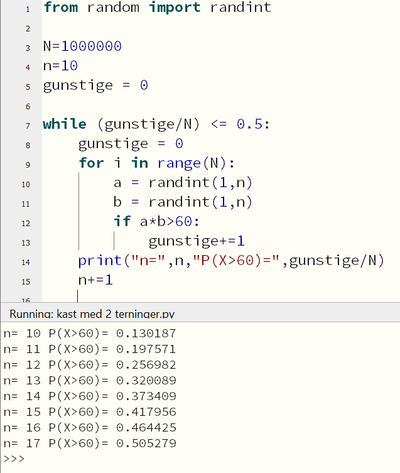
===b)=== | |||
[[File: S1-H22-del2-6b2.png|400px]] | |||
Den minste verdien n kan ha er 17. | |||
==Oppgave 5== | |||
===a)=== | |||
===b)=== | |||
==Oppgave 6== | |||
===a)=== | |||
===b)=== | |||
=== | ===c)=== | ||
===d)=== | |||
=== | ===e)=== | ||
Siste sideversjon per 24. mai 2023 kl. 18:35
Diskusjon av denne oppgaven på matteprat
Løysing laga av Torodd F. Ottestad
DEL EN
Oppgave 1
$(2a^{-2} b)^{-1} \cdot ({\frac{b^2}{a}})^2 =$ $\frac{a^2}{2b} \cdot \frac{b^4}{a^2}= \frac{b^3}{2} $
Oppgave 2
a)
$ O(x)= -0.05x^2+100x-10000$
$O'(x) = -0,10x+100$
$O'(500)= -50 +100 =50$
Den momentane veksten ved 500 produserte enheter er 50 kr. Det betyr at dersom produksjonen øker med en enhet vil overskuddet øke med 50 kr.
b)
Overskuddsfunksjonen er en parabel som vender sin hule side ned. Den har da et maksimum for O'(x) = 0:
$-0.10x + 100 = 0$
$x=1000$
O(1000) = 40 000 kroner.
Oppgave 3
$\lg(x+3)+\lg x =1$
$\lg((x+3)x) =1$
$10^{\lg(x^2+3x)} = 10^1$
$x^2-3x-10 =0$
$x=5$
(kun positiv løsn. pga log)
Oppgave 4
$\lim\limits_{h \to 0} \frac{(4+h)^2-4^2}{h}$
Dette ser i utgangspunktet ut som et null over null utrykk. Vi får rydde litt:
$\lim\limits_{h \to 0} \frac{(16+8h+ h^2)-16}{h} = \lim\limits_{h \to 0} \frac{h(8+ h)}{h} =8 $
Oppgave 5
a)
Dersom ikke begge kulene er sorte er minst en hvit.
P(minst en hvit) = 1 - P(to sorte) = 1 - $\frac{6}{8} \cdot \frac{5}{7} = \frac{13}{28}$
b)
antall hvite kuler (h) = 2
antall svarte kuler (s) = 0
sannsynligheten (P) for å trekke 2 svarte kuler = 0
Så lenge (while) sannsynligheten er mindre enn 0,5:
- legge til 1 svart kule (s=s+1)
- $P=\frac{s}{h+s}\cdot\frac{s-1}{h+s-1}$
- når løkken er ferdig: skrive ut verdien for antall svarte kuler, og sannsynligheten for å trekke to svarte kuler.
DEL TO
Oppgave 1
Dette kan oppfattes som en binomisk situasjon
- Om hendelsen inntreffer eller ikke: turist eller ikke.
- Vi regner sannsynligheten som lik i alle delforsøk, fordi det er mange turister.
- Delforsøkene er uavhengige. (Dette er neppe helt riktig)
Det er ca. 65% sannsynlig.
Oppgave 2
a)
Definerer x
- Finer tangenten g(x) i et vilkårlig punkt a
- Finner tangentens skjæringer med aksene
- Finner uttrykket for arealet
Arealet av trekanten blir ca. 0,78 (linje 6) når koordinatene til P er $( \frac 12, \frac 34)$
b)
Vi deriverer arealfunksjonen og setter den lik null, løser likningen. Se linje 8 og 9 i del a. Minste areal ca. 0,77.
Oppgave 3
a)
Å basere en "modell" på historiske data og forvente at den skal gi et bilde av fremtiden er omtrent som å tro på julenissen. For å si noe om framtiden trenger vi informasjon og forutsetninger utover historiske data.
Begge grafene gir et bilde av det som har vært. Polynomfunksjonen gir best sammenheng med en kvadrert regresjonskoeffisient på 0,9917. Begge funksjoner vokser med en takt som neppe er bærekraftig. Polynomfunksjonen vokser minst og vil trolig ligge nærmest den framtidige virkelighet, selv om oppgaven mangler informasjon til å kunne si noe fornuftig om det.
b)
Veksten er 33 og 91 milliarder per å i gjennomsnitt for henholdsvis g og f.
c)
d)
Oppgave 4
a)
$P(X>60)\approx 0,13$
b)
Den minste verdien n kan ha er 17.