S1 2020 høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
m →c): Det skal være -5/2 og ikke 5/2. Personen skrev det tidligere, men glemte sikkert å skrive det på slutten. |
||
| (51 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 4: | Linje 4: | ||
[https://matematikk.net/matteprat/download/file.php?id=3257 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | [https://matematikk.net/matteprat/download/file.php?id=3257 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | ||
[https://youtu.be/dnAHD6Q3HCI Videoløsning del 1 av Lektor Lainz] | |||
=DEL 1= | |||
==Oppgave 1== | |||
===a)=== | |||
$2(3x+2)=2x(x+2)+4 \\ 6x+4 = 2x^2+4x+4 \\ -2x^2+2x=0 \quad |:(-2)\\ x^2-x = 0 \\ x(x-1)=0 \\ x=0 \vee x=1 $ | |||
===b)=== | |||
$3^x\cdot 3^2=\frac{1}{3^5} \\ 3^{x+2}=3^{-5} \\ x+2=-5 \\ x=-7$ | |||
===c)=== | |||
$lg(3x-2)=2lgx \\ lg(3x-2)=lg(x^2) \\ 10^{lg(3x-2)}=10^{lg(x^2)} \\ 3x-2 = x^2 \\ -x^2+3x-2=0 \quad | :(-1)\\ x^2-3x+2=0 \\ (x-1)(x-2)=0 \\ x=1 \vee x=2$ | |||
==Oppgave 2== | |||
===a)=== | |||
$\frac{4a^3(a^{-2}b^3)^2}{(2^{-1})^{-2}ab^4} \\ =\frac{4a^3\cdot a^{-4}\cdot b^6}{2^2\cdot ab^4} \\ = a^{3-4-1}\cdot b^{6-4} \\ = a^{-2}\cdot b^{2} \\ = (\frac{b}{a})^2 $ | |||
===b)=== | |||
$\frac{1}{x-1}-\frac{2x}{x^2-1}+1 \\ = \frac{x+1}{(x+1)(x-1)}-\frac{2x}{(x+1)(x-1)}+\frac{(x+1)(x-1)}{(x+1)(x-1)} \\ = \frac{x+1-2x+(x^2-1)}{(x+1)(x-1)} \\ = \frac{x^2-x}{(x+1)(x-1)} \\ = \frac{x(x-1)}{(x+1)(x-1)} \\ = \frac{x}{x+1}$ | |||
==Oppgave 3== | |||
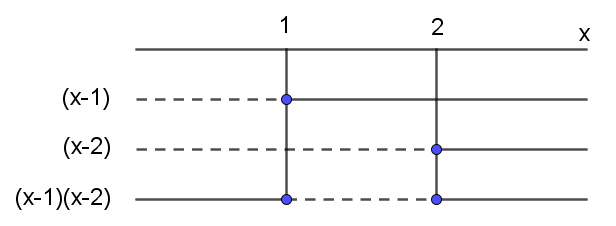
$x^2-3x+2\leq 0 \\ (x-1)(x-2)\leq 0$ | |||
Nullpunkter: $x=1$ og $x=2$ | |||
[[File: S1_H20_del1_3.png]] | |||
$x^2-3x+2\leq 0$ når $x\in [1,2]$ | |||
==Oppgave 4== | |||
La $x$ være antall gullmedaljer, og $y$ være antall sølvmedaljer. | |||
$I \quad x+y=16 \\ II \quad 7x+5y=102$ | |||
$I \quad y=16-x$ | |||
$II \quad 7x+5(16-x)=102 \\ \quad \quad 7x+80-5x=102 \\ \quad \quad 2x=102-80 \\ \quad \quad x=\frac{22}{2}=11$ | |||
Norge tok 11 gullmedaljer i vinter-OL i 2014. | |||
==Oppgave 5== | |||
===a)=== | |||
$P(to \, like)=P((B\cap B)\cup(R\cap R))= \frac{2}{4}\cdot \frac{1}{3}+\frac{2}{4}\cdot \frac{1}{3} = \frac{2}{12}+\frac{2}{12}=\frac{4}{12}=\frac{1}{3}$ | |||
Sannsynligheten for at Mia må ta oppvasken dersom de følger dette forslaget er $\frac{1}{3}$. | |||
===b)=== | |||
La $x$ være antall røde kuler. | |||
$P(to\, ulike)=P((B\cap R)\cup(R\cap B)) \\ = \frac{2}{2+x}\cdot \frac{x}{2+x-1} + \frac{x}{2+x} \cdot \frac{2}{2+x-1} \\ = \frac{2x}{(2+x)(1+x)}\cdot 2 \\ = \frac{4x}{x^2+2x+x+2} \\ = \frac{4x}{x^2+3x+2}$ | |||
Setter $P(to\,ulike) < \frac{1}{2}$ | |||
$\frac{4x}{x^2+3x+2} < \frac{1}{2} \\ 8x < x^2+3x+2 \\ -x^2+5x-2 < 0 \\ x^2-5x+2 > 0 \\ x>\frac{5\pm\sqrt{25-4\cdot 1 \cdot 2}}{2} \\ x_1> \frac{5+\sqrt{17}}{2} \vee x_2>\frac{5-\sqrt{17}}{2}$ | |||
Velger den positive løsningen, $x_1$. Vi vet at $\sqrt{17} > 4$, siden $\sqrt{16}=4$. | |||
$x_1 > \frac{5+4}{2} \\ x_1 > 4,5$ | |||
Det må ligge flere enn 5 røde kuler i krukken, dersom sannsynligheten for at de to kulene som trekkes har ulik farge, er mindre enn 50 %. | |||
==Oppgave 6== | |||
$\bullet$ Vi har en vertikal asymptote i x = 3. Det vil si at nevner er lik null når x = 3. | |||
$\quad 3+c = 0 \Rightarrow c=-3$ | |||
$\bullet$ Vi lar x gå mot uendelig: | |||
$\quad lim_{x \to \infty} \frac{ax+b}{x+c} \approx lim_{x \to \infty} \frac{ax}{x} = a $ | |||
$\quad $ Vi har en horisontal asymptote i y = -2, og har derfor $a=-2$ | |||
$\bullet$ Ser at vi har et nullpunkt i x=2. Setter $f(x)=0$ | |||
$\quad \frac{ax+b}{x+c}=0 \\ \quad \frac{-2\cdot 2+b}{x-3}=0 \\ \quad -4+b = 0 \\ \quad b=4 $ | |||
Vi har $a = -2$, $b = 4$ og $c = -3$. | |||
==Oppgave 7== | |||
===a)=== | |||
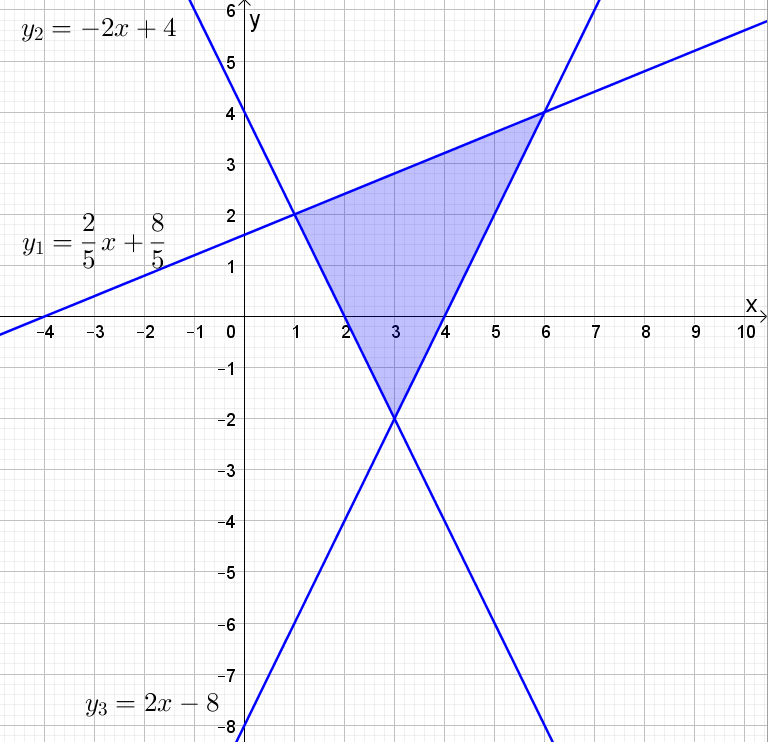
Skriver om ulikhetene på formen y=ax+b. Tegner inn disse linjene i et koordinatsystem (du må gjøre det for hånd). | |||
$-2x+5y \leq 8 \quad \Rightarrow \quad y \leq \frac{2}{5}x+\frac{8}{5} \quad \Rightarrow \quad y \leq 0,4x+1,6$ | |||
$2x+y \geq 4 \quad \Rightarrow \quad y \geq -2x+4$ | |||
$2x-y \leq 8 \quad \Rightarrow \quad y \geq 2x-8 $ | |||
[[File: S1_H20_del1_7-2.png]] | |||
===b)=== | |||
Regner ut verdien til uttrykket $-2x+3y$ i hjørnene: | |||
Hjørnet (1,2): $-2\cdot 1+3\cdot 2 = -2+6=4$ | |||
Hjørnet (3,-2): $-2\cdot 3 + 3\cdot (-2) = -6-6 = -12$ | |||
Hjørnet (6,4): $-2\cdot 6 + 3\cdot 4 = -12+12 = 0$ | |||
Uttrykket $-2x+3y$ kan få alle verdier i intervallet $[-12,4]$, dersom (x,y) skal ligge i <i>M</i>. | |||
==Oppgave 8== | |||
$g(x) = x^3-\frac{3}{2}x^2$ | |||
===a)=== | |||
$g(\frac{3}{2})=(\frac{3}{2})^3-\frac{3}{2}\cdot (\frac{3}{2})^2=(\frac{3}{2})^3-(\frac{3}{2})^3=0$ | |||
$g(2)=2^3-\frac{3}{2}\cdot 2^2 = 8-3\cdot 2 = 8-6 = 2 $ | |||
Gjennomsnittlig vekstfart: | |||
$\frac{y_2-y_1}{x_2-x_1}=\frac{2-0}{2-\frac{3}{2}} = \frac{2}{0,5} = 4$ | |||
Den gjennomsnittlige vekstfarten til <i>g</i> i intervallet $[\frac{3}{2},2]$ er 4. | |||
===b)=== | |||
$g'(x)=3x^2-\frac{3\cdot 2}{2}x = 3x^2-3x$ | |||
$g'(2)=3\cdot 2^2-3\cdot 2 = 12-6 = 6$ | |||
===c)=== | |||
Setter $g'(x)=6$ | |||
$3x^2-3x = 6 \\ 3x^2-3x-6 = 0 \quad |:3 \\ x^2-x-2 = 0 \\ (x+1)(x-2)=0 \\ x_1=-1 \vee x_2 = 2$ | |||
$g(-1) = (-1)^3-\frac{3}{2}\cdot (-1)^2 = -1-\frac{3}{2} = -\frac{2}{2}-\frac{3}{2} = -\frac{5}{2}$ | |||
$g(2) = 2$, som vi regnet ut i a). | |||
$A=(-1, -\frac{5}{2})$ og $B=(2,2)$. | |||
==Oppgave 9== | |||
===a)=== | |||
Vi har omkretsen til rektangelet $O=2x+2y = 96\,cm$ | |||
$2x+2y=96 \\ y = \frac{96-2x}{2} \\ y= 48-x$ | |||
===b)=== | |||
Vi trenger et uttrykk for radiusen til sylinderen. Vi har omkretsen til sylinderen $O=2\pi r = x$ | |||
$2\pi r = x \quad \Rightarrow \quad r = \frac{x}{2\pi}$ | |||
Volumet av en sylinder: $V=\pi r^2\cdot h$ | |||
$V(x)=\pi (\frac{x}{2\pi})^2 \cdot (48-x) \\ = \pi (\frac{x^2}{4 \pi ^2})\cdot (48-x) \\ = \frac{x^2}{4\pi}(48-x) \\ = \frac{1}{4\pi}(48x^2-x^3)$ | |||
===c)=== | |||
$V'(x)=\frac{1}{4\pi}(96x - 3x^2)$ | |||
Setter $V'(x)=0$ | |||
$\frac{1}{4\pi}(96x - 3x^2)=0 \\ 96x-3x^2 = 0 \\ x(96-3x)=0 \\ x_1=0 \vee x_2 = \frac{96}{3}=32$ | |||
Vi kan ikke ha en omkrets x=0, så vi må ha omkretsen x=32 for at volumet av sylinderen skal bli størst mulig. | |||
Notat: andregradsleddet til den deriverte har negativt fortegn, så den deriverte er en andregradsfunksjon som vender den hule siden ned. Det vil si at V'(x) er positiv i intervallet $x\in[0,32]$, så funksjonen V(x) vokser i dette intervallet, og vi vet derfor at vi har et toppunkt i x=32 (og ikke et bunnpunkt). | |||
=DEL 2= | |||
===a)=== | |||
Sannsynligheten for at det er sol en tilfeldig dag på Gran Canaria er $\frac{300}{365}\approx 0,8219$. | |||
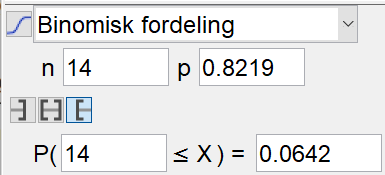
Bruker sannsynlighetskalkulatoren i Geogebra og velger binomisk fordeling. Velger n=14 og p=0,8219, som gir $P(X\geq 14) \approx 0,064$. | |||
[[File: S1_H20_del2_1a.png]] | |||
Agnete har antatt en binomisk fordeling av soldager. Det innebærer at: | |||
$\bullet$ Sannsynligheten for at det er sol en dag er den samme hver dag. | |||
$\bullet$ Sannsynligheten for at det er sol en dag er uavhengig av sannsynligheten for at det er sol en annen dag. | |||
$\bullet$ Det er enten sol eller ikke sol. Hun har ikke tatt høyde for ulike varianter av sol med skyer, sol kun på formiddagen etc. | |||
===b)=== | |||
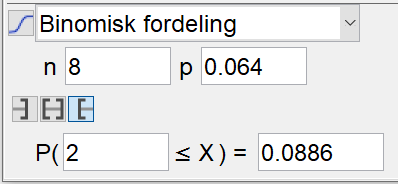
Bruker sannsynlighetskalkulatoren i Geogebra, og velger igjen en binomisk fordeling. Velger n = 8 (antall ferier), og p = 0,064 (sannsynligheten for bare soldager i en ferie). Finner $P(X\geq 2) = 0,0886$. | |||
[[File: S1_H20_del2_1b.png]] | |||
Det er 8,86 % sannsynlighet for at familien opplever bare soldager på minst 2 av sine 8 ferier på Gran Canaria. | |||
===c)=== | |||
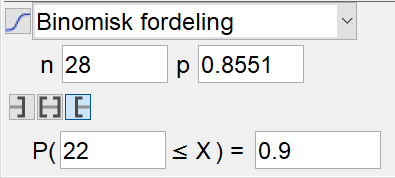
Bruker sannsynlighetskalkulatoren i Geogebra, og velger binomisk fordeling. Velger n = 28 (4 x 7 dager), og prøver meg frem til en sannsynlighet som gir $p(X\geq 22)$. Finner da p=0,8551. | |||
[[File: S1_H20_del2_1c.png]] | |||
$\frac{x}{365}=0,8551 \Rightarrow x =0,8551 \cdot 365 \approx 312,11$ | |||
Det må minst være i gjennomsnitt 313 soldager i året på dette stedet, for at påstanden fra reisebyrået skal være sann. | |||
==Oppgave 2== | |||
===a)=== | |||
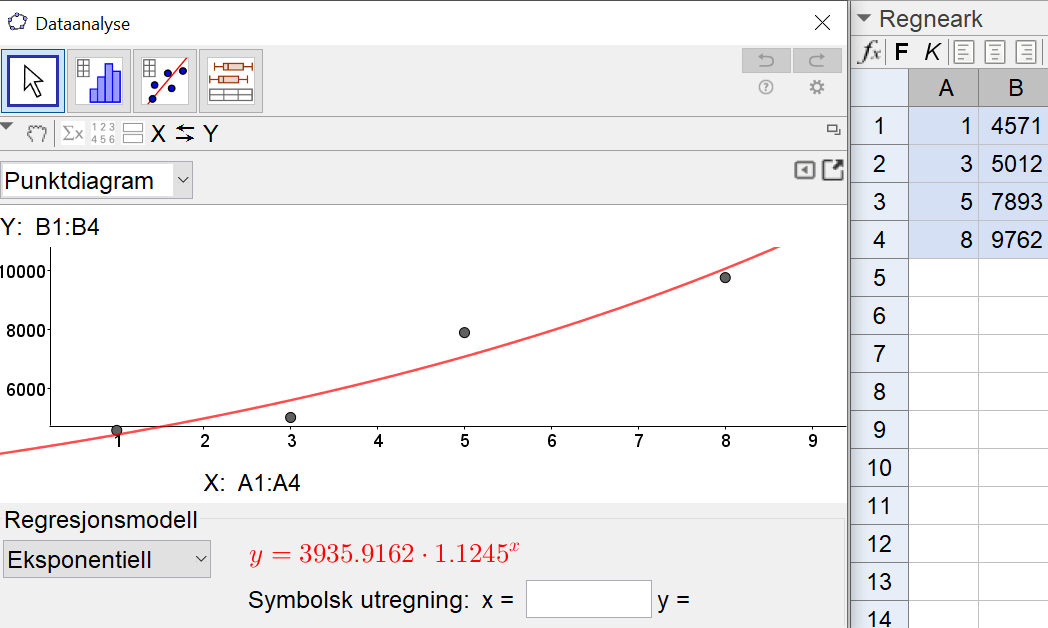
Bruker <i>regresjonsanalyse</i> i Geogebra. | |||
[[File: S1_H20_del2_2a.png]] | |||
$g(x)=3936\cdot 1,125^x$ er en eksponentiell modell for avskogingen i Amazonas (målt i kvadratkilometer) x år etter 2011. | |||
===b)=== | |||
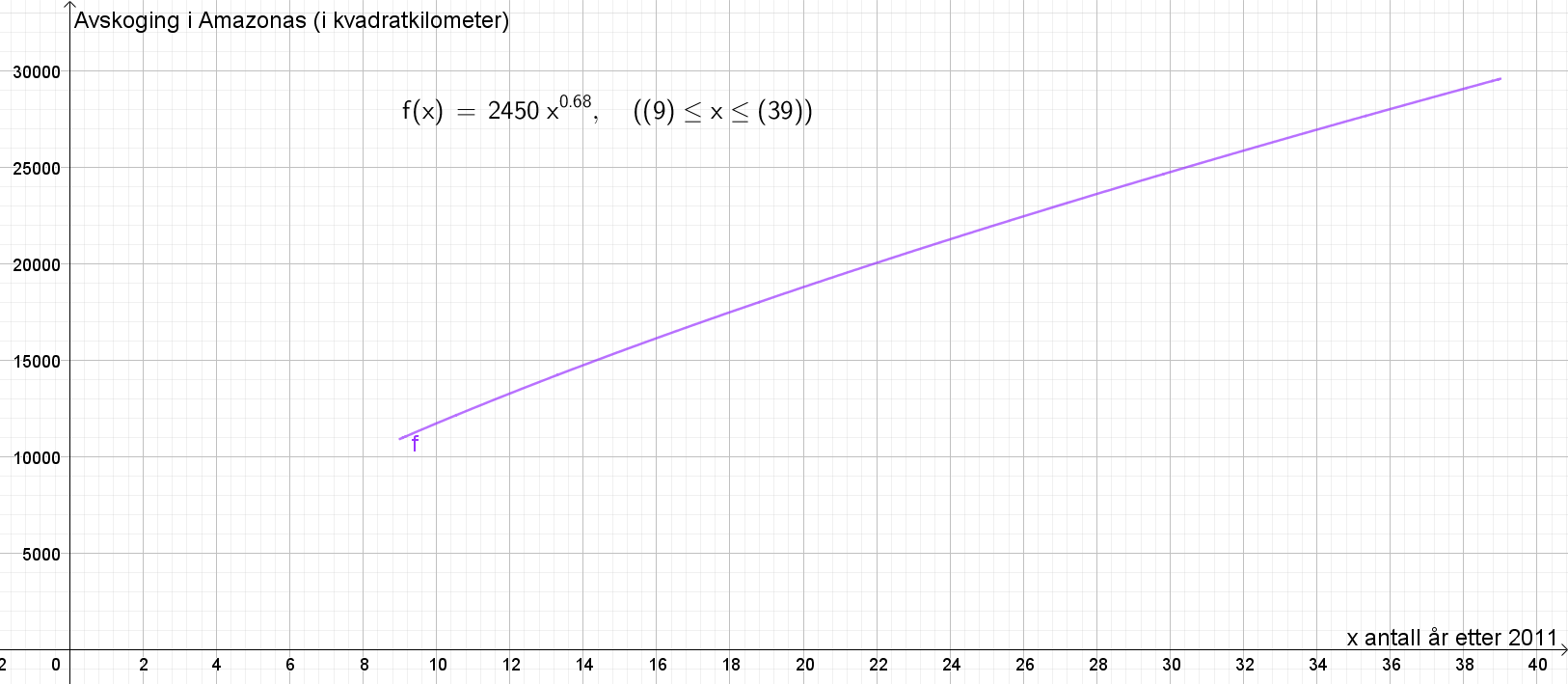
Tegner grafen i Geogebra. | |||
[[File: S1_H20_del2_2b.png]] | |||
===c)=== | |||
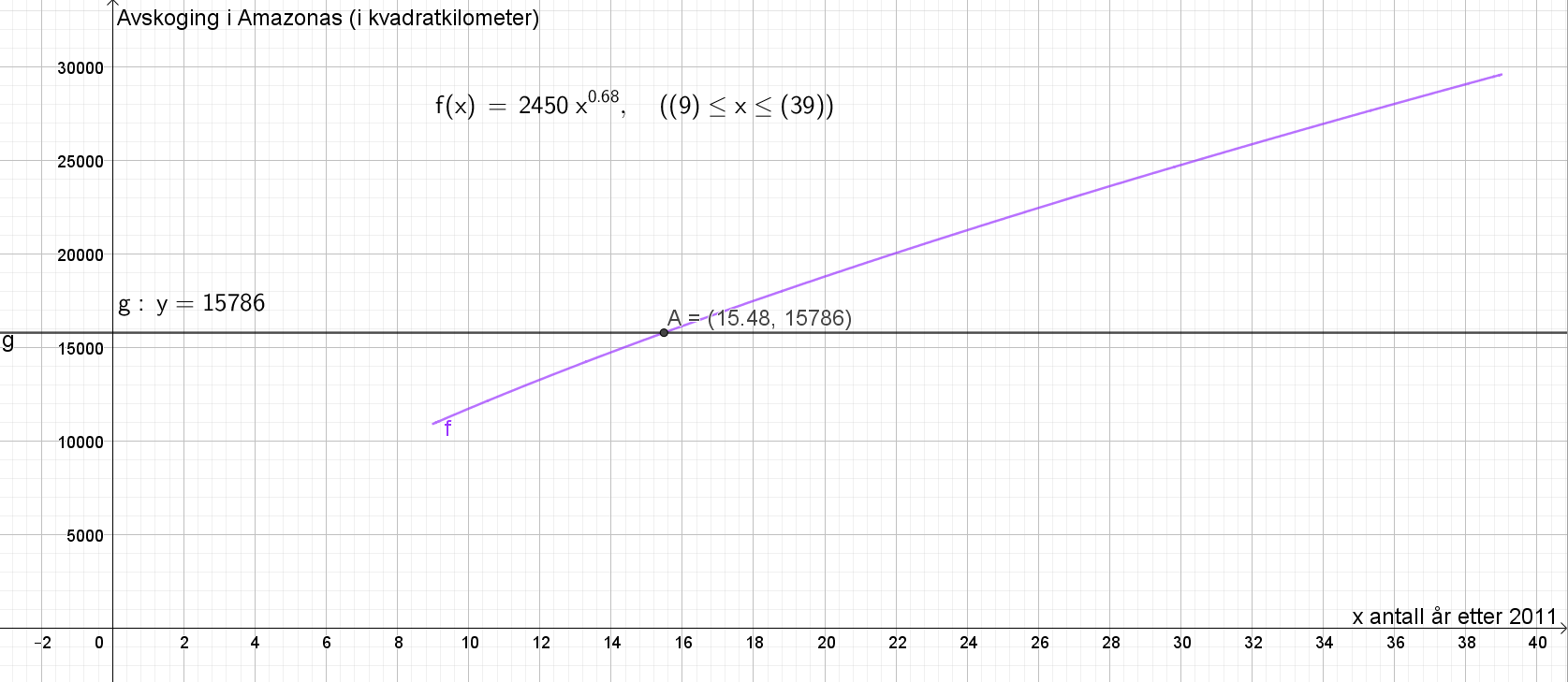
Avskogingen var 7893 kvadratkilometer per år i 2016. Tegner linja $y=2\cdot 7893$, og finner skjæringspunktet med grafen til f (se punkt A). | |||
[[File: S1_H20_del2_2c.png]] | |||
15,48 år etter 2011, det vil si i løpet av år 2026, vil avskogingen per år for første gang være mer enn dobbelt så stor som avskogingen var i 2016, ifølge modellen f. | |||
===d)=== | |||
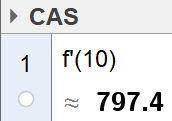
Bruker CAS i Geogebra til å finne f'(10). | |||
[[File: S1_H20_del2_2d.png]] | |||
Dette forteller oss at 10 år etter 2011, altså i år 2021, øker avskogingen med 797,4 kvadratkilometer per år. | |||
==Oppgave 3== | |||
===a)=== | |||
La og være antall marsipanpølser konditoriet produserer hver dag av henholdsvis type A og type B. | |||
Vi har $x\geq 0$ og $y\geq 0$ fordi konditoriet må produsere 0 eller flere marsipanpølser. | |||
Setter opplysningene om marsipanpølsene i en tabell. | |||
{| width="auto" | |||
| | |||
| Type A | |||
| Type B | |||
| Mengde tilgjengelig | |||
|- | |||
| Melis | |||
| $ 50\% \cdot 500\,g = 250\,g$ | |||
| $ 20\% \cdot 500g = 100\,g$ | |||
| $60000\,g$ | |||
|- | |||
| Mandler | |||
| $ 45\% \cdot 500\,g = 225\,g$ | |||
| $ 70\% \cdot 500\,g = 350\,g$ | |||
| $88200\,g$ | |||
|- | |||
| Eggehvite | |||
| $ 5\% \cdot 500\,g = 25\,g$ | |||
| $ 10\% \cdot 500\,g = 50\,g$ | |||
| $12000\,g$ | |||
|} | |||
Leser av for melis i tabellen, at 250 g melis per type A marsipanpølse og 100 g melis per type B marsipanpølse, til sammen må forbruke mindre enn 60000g tilgjengelig melis. | |||
$250x+100y \leq 60000 \Rightarrow 2,5x+y\leq 600$ | |||
Leser av for mandler i tabellen, at 225 g mandler per type A marsipanpølse og 350 g mandler per type B marsipanpølse, til sammen må forbruke mindre enn 88200g tilgjengelig mandler. | |||
$225x+350y \leq 88200 \Rightarrow 2,25x+3,5y\leq 882$ | |||
Leser av for eggehvite i tabellen, at 25 g eggehvite per type A marsipanpølse og 50 g eggehvite per type B marsipanpølse, til sammen må forbruke mindre enn 12000g tilgjengelig eggehvite. | |||
$25x+50y \leq 12000 \Rightarrow x+2y\leq 480$ | |||
===b)=== | |||
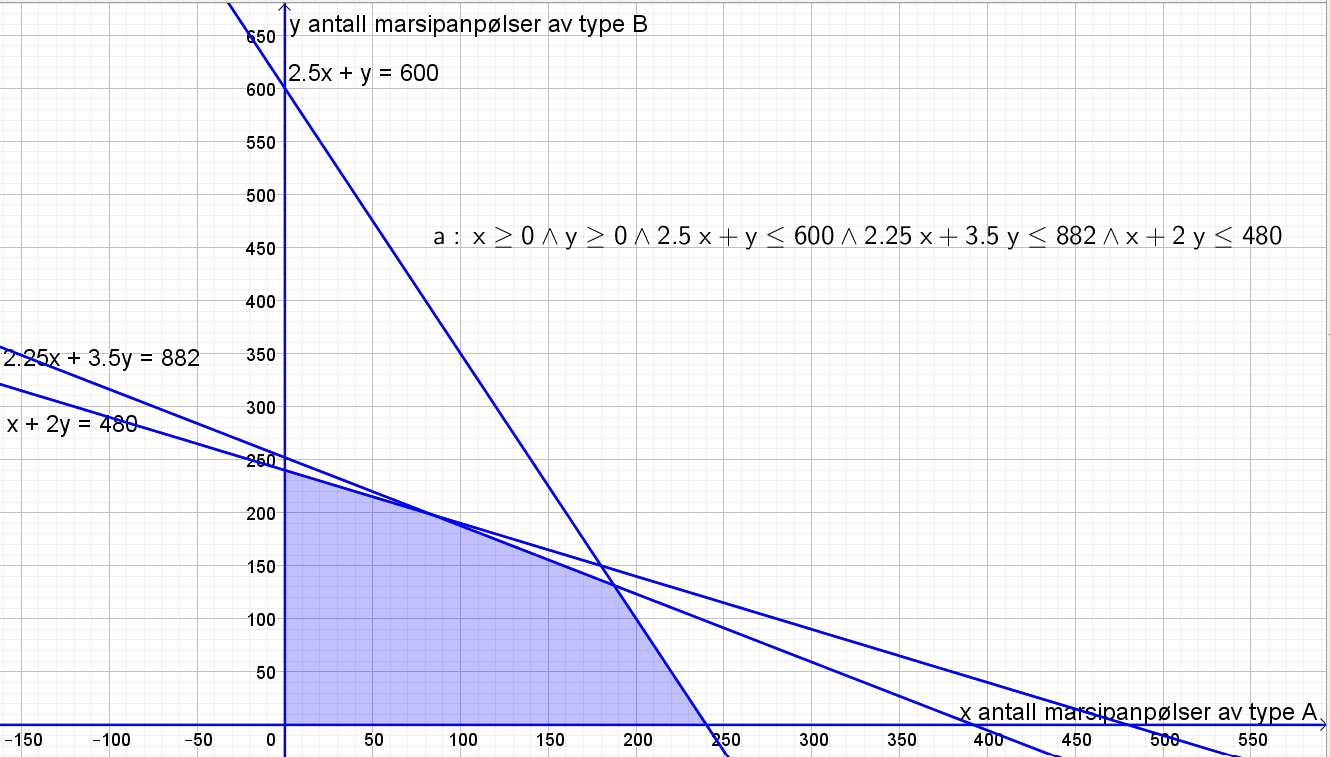
[[File: S1_H20_del2_3b.png]] | |||
===c)=== | |||
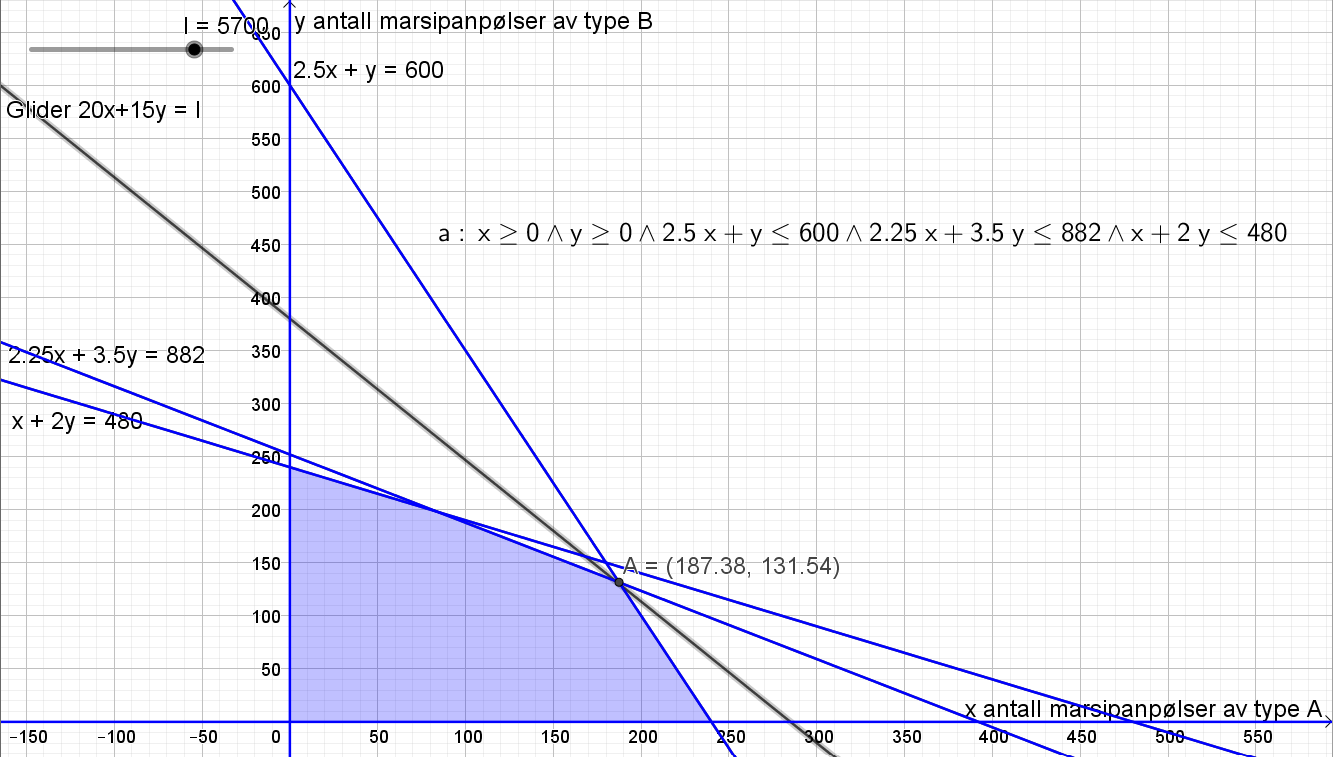
Lager en glider, 20x+15y=I, og finner ut i hvilket hjørne av området fortjenesten er maksimert. Dette er i punkt A, men det går ikke an å produsere et desimaltall antall marsipanpølser. | |||
[[File: S1_H20_del2_3c.png]] | |||
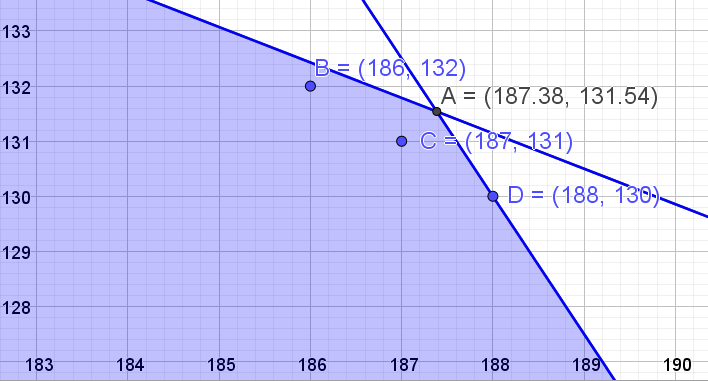
Undersøker de nærmeste punktene med hele antall marsipanpølser, som fortsatt er innenfor det skraverte området. Se punkt B, C og D. | |||
[[File: S1_H20_del2_3c2.png]] | |||
Regner ut maksimal fortjeneste i de ulike punktene: | |||
Punkt B: $20\,kr\cdot 186 + 15\,kr \cdot 132 = 5700\,kr$ | |||
Punkt C: $20\,kr\cdot 187 + 15\,kr \cdot 131 = 5705\,kr$ | |||
Punkt D: $20\,kr\cdot 188 + 15\,kr \cdot 130 = 5710\,kr$ | |||
For å maksimere fortjenesten sin, må konditoriet produsere 188 marsipanpølser av type A, og 130 marsipanpølser av type B. Fortjenesten blir da 5710 kr. | |||
===d)=== | |||
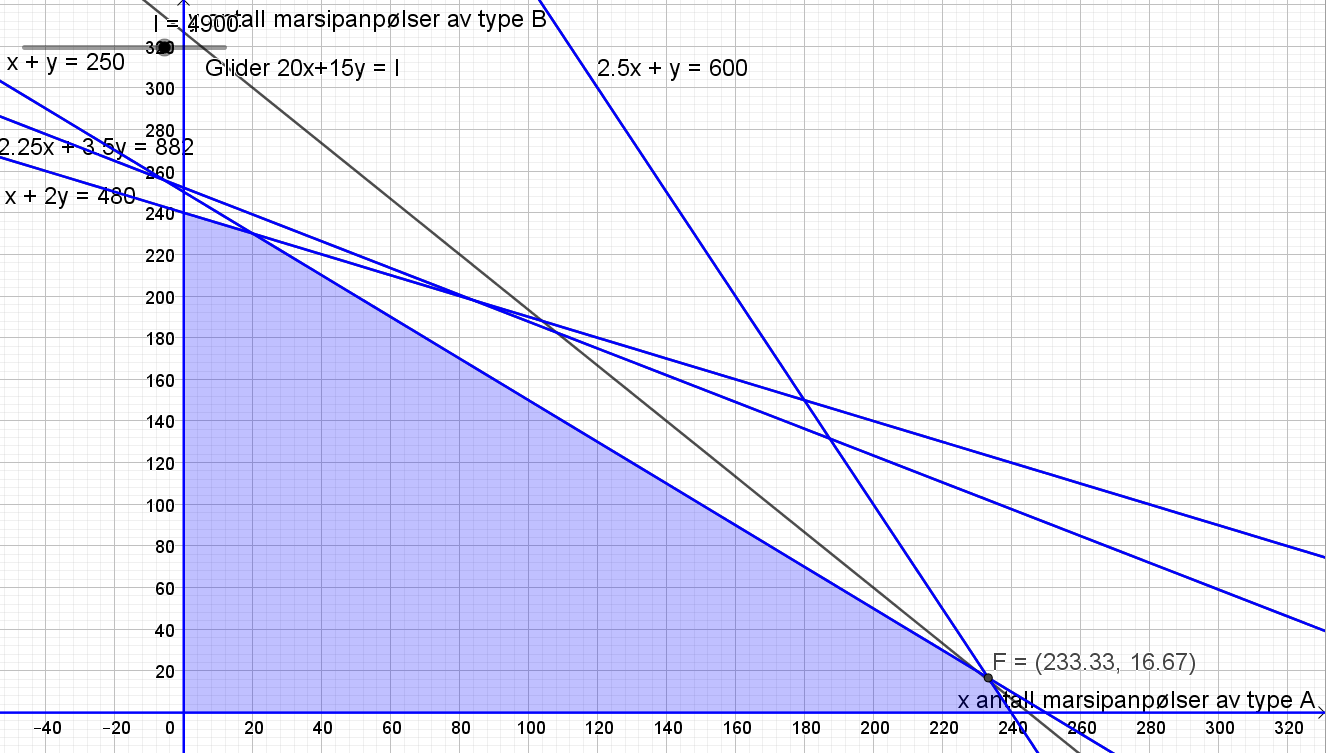
Legger til $x+y\leq 250$ til de andre ulikhetene i Geogebra. Beveger glidere fra oppgave c), og ser at fortjenesten nå er størst i nærheten av punkt F. | |||
[[File: S1_H20_del2_3d.png]] | |||
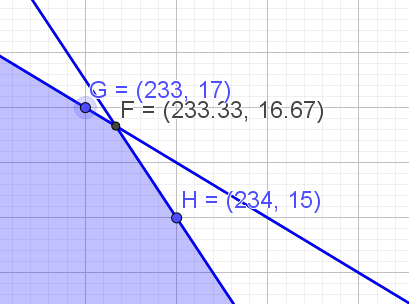
Finner de nærmeste punktene med hele tall som fremdeles er innenfor det skraverte området, og regner ut fortjenesten: | |||
[[File: S1_H20_del2_3d2.png]] | |||
Punkt G: $20\,kr\cdot 233+15\,kr\cdot 17 = 4915\,kr$ | |||
Punkt H: $20\,kr\cdot 234+15\,kr\cdot 15 = 4905\,kr$ | |||
Den største fortjenesten konditoriet klarer å få per dag denne uken er 4915 kr. | |||
Siste sideversjon per 19. mai 2021 kl. 01:41
Diskusjon av denne oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
Videoløsning del 1 av Lektor Lainz
DEL 1
Oppgave 1
a)
$2(3x+2)=2x(x+2)+4 \\ 6x+4 = 2x^2+4x+4 \\ -2x^2+2x=0 \quad |:(-2)\\ x^2-x = 0 \\ x(x-1)=0 \\ x=0 \vee x=1 $
b)
$3^x\cdot 3^2=\frac{1}{3^5} \\ 3^{x+2}=3^{-5} \\ x+2=-5 \\ x=-7$
c)
$lg(3x-2)=2lgx \\ lg(3x-2)=lg(x^2) \\ 10^{lg(3x-2)}=10^{lg(x^2)} \\ 3x-2 = x^2 \\ -x^2+3x-2=0 \quad | :(-1)\\ x^2-3x+2=0 \\ (x-1)(x-2)=0 \\ x=1 \vee x=2$
Oppgave 2
a)
$\frac{4a^3(a^{-2}b^3)^2}{(2^{-1})^{-2}ab^4} \\ =\frac{4a^3\cdot a^{-4}\cdot b^6}{2^2\cdot ab^4} \\ = a^{3-4-1}\cdot b^{6-4} \\ = a^{-2}\cdot b^{2} \\ = (\frac{b}{a})^2 $
b)
$\frac{1}{x-1}-\frac{2x}{x^2-1}+1 \\ = \frac{x+1}{(x+1)(x-1)}-\frac{2x}{(x+1)(x-1)}+\frac{(x+1)(x-1)}{(x+1)(x-1)} \\ = \frac{x+1-2x+(x^2-1)}{(x+1)(x-1)} \\ = \frac{x^2-x}{(x+1)(x-1)} \\ = \frac{x(x-1)}{(x+1)(x-1)} \\ = \frac{x}{x+1}$
Oppgave 3
$x^2-3x+2\leq 0 \\ (x-1)(x-2)\leq 0$
Nullpunkter: $x=1$ og $x=2$
$x^2-3x+2\leq 0$ når $x\in [1,2]$
Oppgave 4
La $x$ være antall gullmedaljer, og $y$ være antall sølvmedaljer.
$I \quad x+y=16 \\ II \quad 7x+5y=102$
$I \quad y=16-x$
$II \quad 7x+5(16-x)=102 \\ \quad \quad 7x+80-5x=102 \\ \quad \quad 2x=102-80 \\ \quad \quad x=\frac{22}{2}=11$
Norge tok 11 gullmedaljer i vinter-OL i 2014.
Oppgave 5
a)
$P(to \, like)=P((B\cap B)\cup(R\cap R))= \frac{2}{4}\cdot \frac{1}{3}+\frac{2}{4}\cdot \frac{1}{3} = \frac{2}{12}+\frac{2}{12}=\frac{4}{12}=\frac{1}{3}$
Sannsynligheten for at Mia må ta oppvasken dersom de følger dette forslaget er $\frac{1}{3}$.
b)
La $x$ være antall røde kuler.
$P(to\, ulike)=P((B\cap R)\cup(R\cap B)) \\ = \frac{2}{2+x}\cdot \frac{x}{2+x-1} + \frac{x}{2+x} \cdot \frac{2}{2+x-1} \\ = \frac{2x}{(2+x)(1+x)}\cdot 2 \\ = \frac{4x}{x^2+2x+x+2} \\ = \frac{4x}{x^2+3x+2}$
Setter $P(to\,ulike) < \frac{1}{2}$
$\frac{4x}{x^2+3x+2} < \frac{1}{2} \\ 8x < x^2+3x+2 \\ -x^2+5x-2 < 0 \\ x^2-5x+2 > 0 \\ x>\frac{5\pm\sqrt{25-4\cdot 1 \cdot 2}}{2} \\ x_1> \frac{5+\sqrt{17}}{2} \vee x_2>\frac{5-\sqrt{17}}{2}$
Velger den positive løsningen, $x_1$. Vi vet at $\sqrt{17} > 4$, siden $\sqrt{16}=4$.
$x_1 > \frac{5+4}{2} \\ x_1 > 4,5$
Det må ligge flere enn 5 røde kuler i krukken, dersom sannsynligheten for at de to kulene som trekkes har ulik farge, er mindre enn 50 %.
Oppgave 6
$\bullet$ Vi har en vertikal asymptote i x = 3. Det vil si at nevner er lik null når x = 3.
$\quad 3+c = 0 \Rightarrow c=-3$
$\bullet$ Vi lar x gå mot uendelig:
$\quad lim_{x \to \infty} \frac{ax+b}{x+c} \approx lim_{x \to \infty} \frac{ax}{x} = a $
$\quad $ Vi har en horisontal asymptote i y = -2, og har derfor $a=-2$
$\bullet$ Ser at vi har et nullpunkt i x=2. Setter $f(x)=0$
$\quad \frac{ax+b}{x+c}=0 \\ \quad \frac{-2\cdot 2+b}{x-3}=0 \\ \quad -4+b = 0 \\ \quad b=4 $
Vi har $a = -2$, $b = 4$ og $c = -3$.
Oppgave 7
a)
Skriver om ulikhetene på formen y=ax+b. Tegner inn disse linjene i et koordinatsystem (du må gjøre det for hånd).
$-2x+5y \leq 8 \quad \Rightarrow \quad y \leq \frac{2}{5}x+\frac{8}{5} \quad \Rightarrow \quad y \leq 0,4x+1,6$
$2x+y \geq 4 \quad \Rightarrow \quad y \geq -2x+4$
$2x-y \leq 8 \quad \Rightarrow \quad y \geq 2x-8 $
b)
Regner ut verdien til uttrykket $-2x+3y$ i hjørnene:
Hjørnet (1,2): $-2\cdot 1+3\cdot 2 = -2+6=4$
Hjørnet (3,-2): $-2\cdot 3 + 3\cdot (-2) = -6-6 = -12$
Hjørnet (6,4): $-2\cdot 6 + 3\cdot 4 = -12+12 = 0$
Uttrykket $-2x+3y$ kan få alle verdier i intervallet $[-12,4]$, dersom (x,y) skal ligge i M.
Oppgave 8
$g(x) = x^3-\frac{3}{2}x^2$
a)
$g(\frac{3}{2})=(\frac{3}{2})^3-\frac{3}{2}\cdot (\frac{3}{2})^2=(\frac{3}{2})^3-(\frac{3}{2})^3=0$
$g(2)=2^3-\frac{3}{2}\cdot 2^2 = 8-3\cdot 2 = 8-6 = 2 $
Gjennomsnittlig vekstfart:
$\frac{y_2-y_1}{x_2-x_1}=\frac{2-0}{2-\frac{3}{2}} = \frac{2}{0,5} = 4$
Den gjennomsnittlige vekstfarten til g i intervallet $[\frac{3}{2},2]$ er 4.
b)
$g'(x)=3x^2-\frac{3\cdot 2}{2}x = 3x^2-3x$
$g'(2)=3\cdot 2^2-3\cdot 2 = 12-6 = 6$
c)
Setter $g'(x)=6$
$3x^2-3x = 6 \\ 3x^2-3x-6 = 0 \quad |:3 \\ x^2-x-2 = 0 \\ (x+1)(x-2)=0 \\ x_1=-1 \vee x_2 = 2$
$g(-1) = (-1)^3-\frac{3}{2}\cdot (-1)^2 = -1-\frac{3}{2} = -\frac{2}{2}-\frac{3}{2} = -\frac{5}{2}$
$g(2) = 2$, som vi regnet ut i a).
$A=(-1, -\frac{5}{2})$ og $B=(2,2)$.
Oppgave 9
a)
Vi har omkretsen til rektangelet $O=2x+2y = 96\,cm$
$2x+2y=96 \\ y = \frac{96-2x}{2} \\ y= 48-x$
b)
Vi trenger et uttrykk for radiusen til sylinderen. Vi har omkretsen til sylinderen $O=2\pi r = x$
$2\pi r = x \quad \Rightarrow \quad r = \frac{x}{2\pi}$
Volumet av en sylinder: $V=\pi r^2\cdot h$
$V(x)=\pi (\frac{x}{2\pi})^2 \cdot (48-x) \\ = \pi (\frac{x^2}{4 \pi ^2})\cdot (48-x) \\ = \frac{x^2}{4\pi}(48-x) \\ = \frac{1}{4\pi}(48x^2-x^3)$
c)
$V'(x)=\frac{1}{4\pi}(96x - 3x^2)$
Setter $V'(x)=0$
$\frac{1}{4\pi}(96x - 3x^2)=0 \\ 96x-3x^2 = 0 \\ x(96-3x)=0 \\ x_1=0 \vee x_2 = \frac{96}{3}=32$
Vi kan ikke ha en omkrets x=0, så vi må ha omkretsen x=32 for at volumet av sylinderen skal bli størst mulig.
Notat: andregradsleddet til den deriverte har negativt fortegn, så den deriverte er en andregradsfunksjon som vender den hule siden ned. Det vil si at V'(x) er positiv i intervallet $x\in[0,32]$, så funksjonen V(x) vokser i dette intervallet, og vi vet derfor at vi har et toppunkt i x=32 (og ikke et bunnpunkt).
DEL 2
a)
Sannsynligheten for at det er sol en tilfeldig dag på Gran Canaria er $\frac{300}{365}\approx 0,8219$.
Bruker sannsynlighetskalkulatoren i Geogebra og velger binomisk fordeling. Velger n=14 og p=0,8219, som gir $P(X\geq 14) \approx 0,064$.
Agnete har antatt en binomisk fordeling av soldager. Det innebærer at:
$\bullet$ Sannsynligheten for at det er sol en dag er den samme hver dag.
$\bullet$ Sannsynligheten for at det er sol en dag er uavhengig av sannsynligheten for at det er sol en annen dag.
$\bullet$ Det er enten sol eller ikke sol. Hun har ikke tatt høyde for ulike varianter av sol med skyer, sol kun på formiddagen etc.
b)
Bruker sannsynlighetskalkulatoren i Geogebra, og velger igjen en binomisk fordeling. Velger n = 8 (antall ferier), og p = 0,064 (sannsynligheten for bare soldager i en ferie). Finner $P(X\geq 2) = 0,0886$.
Det er 8,86 % sannsynlighet for at familien opplever bare soldager på minst 2 av sine 8 ferier på Gran Canaria.
c)
Bruker sannsynlighetskalkulatoren i Geogebra, og velger binomisk fordeling. Velger n = 28 (4 x 7 dager), og prøver meg frem til en sannsynlighet som gir $p(X\geq 22)$. Finner da p=0,8551.
$\frac{x}{365}=0,8551 \Rightarrow x =0,8551 \cdot 365 \approx 312,11$
Det må minst være i gjennomsnitt 313 soldager i året på dette stedet, for at påstanden fra reisebyrået skal være sann.
Oppgave 2
a)
Bruker regresjonsanalyse i Geogebra.
$g(x)=3936\cdot 1,125^x$ er en eksponentiell modell for avskogingen i Amazonas (målt i kvadratkilometer) x år etter 2011.
b)
Tegner grafen i Geogebra.
c)
Avskogingen var 7893 kvadratkilometer per år i 2016. Tegner linja $y=2\cdot 7893$, og finner skjæringspunktet med grafen til f (se punkt A).
15,48 år etter 2011, det vil si i løpet av år 2026, vil avskogingen per år for første gang være mer enn dobbelt så stor som avskogingen var i 2016, ifølge modellen f.
d)
Bruker CAS i Geogebra til å finne f'(10).
Dette forteller oss at 10 år etter 2011, altså i år 2021, øker avskogingen med 797,4 kvadratkilometer per år.
Oppgave 3
a)
La og være antall marsipanpølser konditoriet produserer hver dag av henholdsvis type A og type B.
Vi har $x\geq 0$ og $y\geq 0$ fordi konditoriet må produsere 0 eller flere marsipanpølser.
Setter opplysningene om marsipanpølsene i en tabell.
| Type A | Type B | Mengde tilgjengelig | |
| Melis | $ 50\% \cdot 500\,g = 250\,g$ | $ 20\% \cdot 500g = 100\,g$ | $60000\,g$ |
| Mandler | $ 45\% \cdot 500\,g = 225\,g$ | $ 70\% \cdot 500\,g = 350\,g$ | $88200\,g$ |
| Eggehvite | $ 5\% \cdot 500\,g = 25\,g$ | $ 10\% \cdot 500\,g = 50\,g$ | $12000\,g$ |
Leser av for melis i tabellen, at 250 g melis per type A marsipanpølse og 100 g melis per type B marsipanpølse, til sammen må forbruke mindre enn 60000g tilgjengelig melis.
$250x+100y \leq 60000 \Rightarrow 2,5x+y\leq 600$
Leser av for mandler i tabellen, at 225 g mandler per type A marsipanpølse og 350 g mandler per type B marsipanpølse, til sammen må forbruke mindre enn 88200g tilgjengelig mandler.
$225x+350y \leq 88200 \Rightarrow 2,25x+3,5y\leq 882$
Leser av for eggehvite i tabellen, at 25 g eggehvite per type A marsipanpølse og 50 g eggehvite per type B marsipanpølse, til sammen må forbruke mindre enn 12000g tilgjengelig eggehvite.
$25x+50y \leq 12000 \Rightarrow x+2y\leq 480$
b)
c)
Lager en glider, 20x+15y=I, og finner ut i hvilket hjørne av området fortjenesten er maksimert. Dette er i punkt A, men det går ikke an å produsere et desimaltall antall marsipanpølser.
Undersøker de nærmeste punktene med hele antall marsipanpølser, som fortsatt er innenfor det skraverte området. Se punkt B, C og D.
Regner ut maksimal fortjeneste i de ulike punktene:
Punkt B: $20\,kr\cdot 186 + 15\,kr \cdot 132 = 5700\,kr$
Punkt C: $20\,kr\cdot 187 + 15\,kr \cdot 131 = 5705\,kr$
Punkt D: $20\,kr\cdot 188 + 15\,kr \cdot 130 = 5710\,kr$
For å maksimere fortjenesten sin, må konditoriet produsere 188 marsipanpølser av type A, og 130 marsipanpølser av type B. Fortjenesten blir da 5710 kr.
d)
Legger til $x+y\leq 250$ til de andre ulikhetene i Geogebra. Beveger glidere fra oppgave c), og ser at fortjenesten nå er størst i nærheten av punkt F.
Finner de nærmeste punktene med hele tall som fremdeles er innenfor det skraverte området, og regner ut fortjenesten:
Punkt G: $20\,kr\cdot 233+15\,kr\cdot 17 = 4915\,kr$
Punkt H: $20\,kr\cdot 234+15\,kr\cdot 15 = 4905\,kr$
Den største fortjenesten konditoriet klarer å få per dag denne uken er 4915 kr.