R2 2020 vår LØSNING: Forskjell mellom sideversjoner
mIngen redigeringsforklaring |
|||
| (44 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 11: | Linje 11: | ||
[https://matematikk.net/matteprat/download/file.php?id=3147 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | [https://matematikk.net/matteprat/download/file.php?id=3147 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | ||
[https://www.youtube.com/playlist?list=PLplkS_rtcCHW9hzWiGQzuobHhr2u8K5ib Videoløsninger Del 1 laget av Lektor Håkon Raustøl] | |||
[https://www.youtube.com/playlist?list=PLplkS_rtcCHUV_vo_3NPrmryBaimxrPej Videoløsninger Del 2 laget av Lektor Håkon Raustøl] | |||
[https://youtu.be/OKqer4YcKlA Videoløsning del 1 laget av Lektor Lainz] | |||
[https://youtu.be/Lnr86AB5Rhs Videoløsning del 2 av Lektor Lainz] | |||
=DEL 1= | =DEL 1= | ||
| Linje 72: | Linje 80: | ||
Finner summen av de 10 første leddene: | Finner summen av de 10 første leddene: | ||
$S_{10} = \frac{a_1+ | $S_{10} = \frac{a_1+a_{10}}{2}\cdot 10 \ S_{10} = \frac{3+39}{2}\cdot 10 \ S_{10} = 210$ | ||
===b)=== | ===b)=== | ||
| Linje 115: | Linje 123: | ||
===b)=== | ===b)=== | ||
Skjæring med y-aksen: | |||
Grafen til | |||
Skjæring med x-aksen; setter | |||
Grafen til | |||
===c)=== | |||
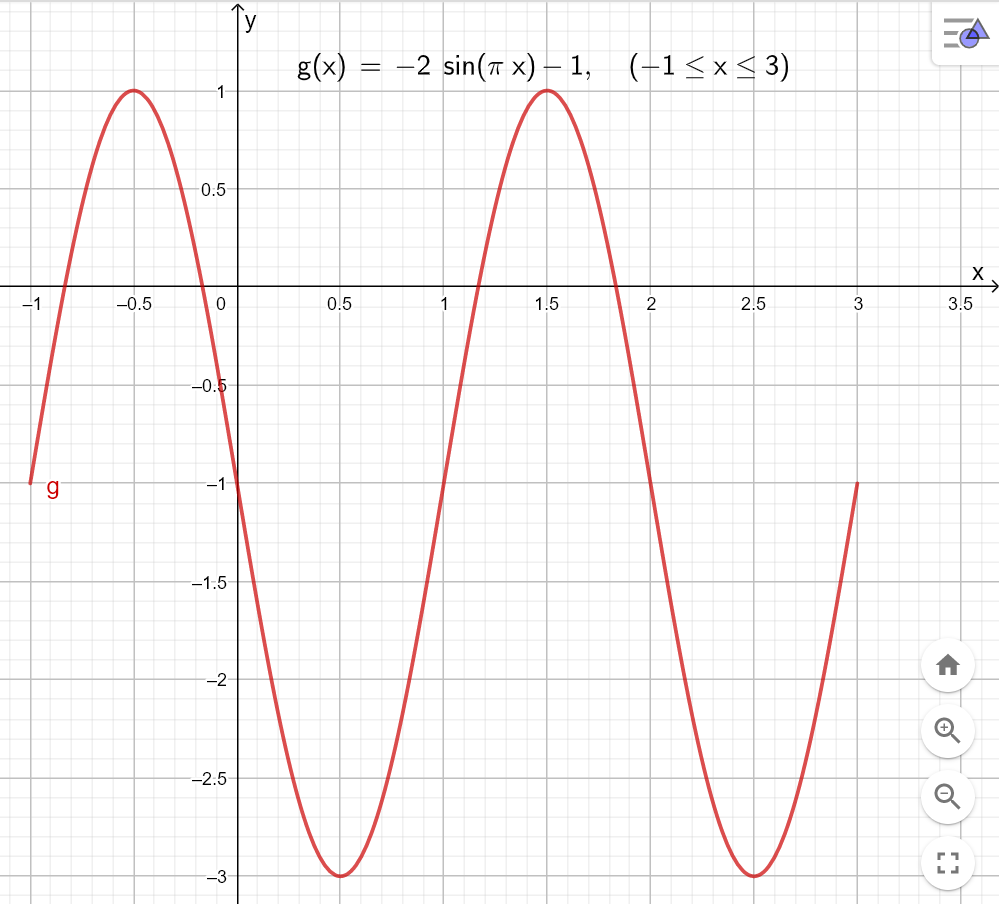
Bruk ekstremalpunktene og nullpunktene, samt skjæring med y-aksen, til å lage en skisse for hånd. | |||
[[File: R2_V20_del1_4c.png]] | |||
==Oppgave 5== | |||
Vi har punktene <i> A(-1,3,2), B(2,2,1), C(0,1,0) </i> og <i> T(5,3,8). </i> | |||
===a)=== | |||
===b)=== | |||
Volumet av pyramiden <i>ABCT</i> er 5. | |||
===c)=== | |||
Likningen for et plan er | |||
Der a, b og c er koordinatene til planets normalvektor, og | |||
Vi har planets normalvektor | |||
Vi får da likning for planet som inneholder punktene A, B og C: | |||
==Oppgave 6== | |||
En uendelig geometrisk rekke er gitt ved | |||
===a)=== | |||
Vi har kvotienten | |||
og | |||
Rekken konvergerer når | |||
===b)=== | |||
Summen av rekken er gitt ved | |||
Summen av rekken blir 4 når | |||
==Oppgave 7== | |||
Vi har differensiallikningen | |||
Sjekker stigningstallet til tangenten i hvert av punktene: | |||
Punkt A(2,2): | |||
Punkt B(-2,2): | |||
Punkt C(-2,-2): | |||
Punkt D(2,-2): | |||
Den markerte tangentretningen samsvarer med retningen til tangenten til integralkurven som går gjennom punkt B og C, men ikke A og D. I punkt A viser den markerte tangentretningen stigningstall 0, og i punkt D stigningstall | |||
==Oppgave 8== | |||
Linje | |||
$l: \left[ \begin{align*} | |||
x &=-3-2s \ | |||
y &= 7+2s \ | |||
z &= -1-s \end{align*}\right]$ | |||
Linja | |||
$m: \left[ \begin{align*} | |||
x &=-4-7t \ | |||
y &= 5+4t \ | |||
z &= -2-4t \end{align*}\right]$ | |||
Skjæringspunktet mellom linje | |||
Finner et uttrykk for s: | |||
Setter inn uttrykket for s i likning | |||
Setter inn uttrykket for t i uttrykket for s fra likning | |||
Setter inn t = -1 i parameterfremstillingen for linje | |||
Sentrum i kula er <i>S(3,1,2)</i>. Bestemmer radius til kula: | |||
Radius i kula er 9. Finner likning for kuleflaten: | |||
==Oppgave 9== | |||
En følge er gitt ved | |||
1. Induksjonsgrunnlag: | |||
2. Induksjonstrinnet: Vi antar at | |||
Vi har | |||
Hvilket skulle vises. | |||
=DEL 2= | |||
==Oppgave 1== | |||
===a)=== | |||
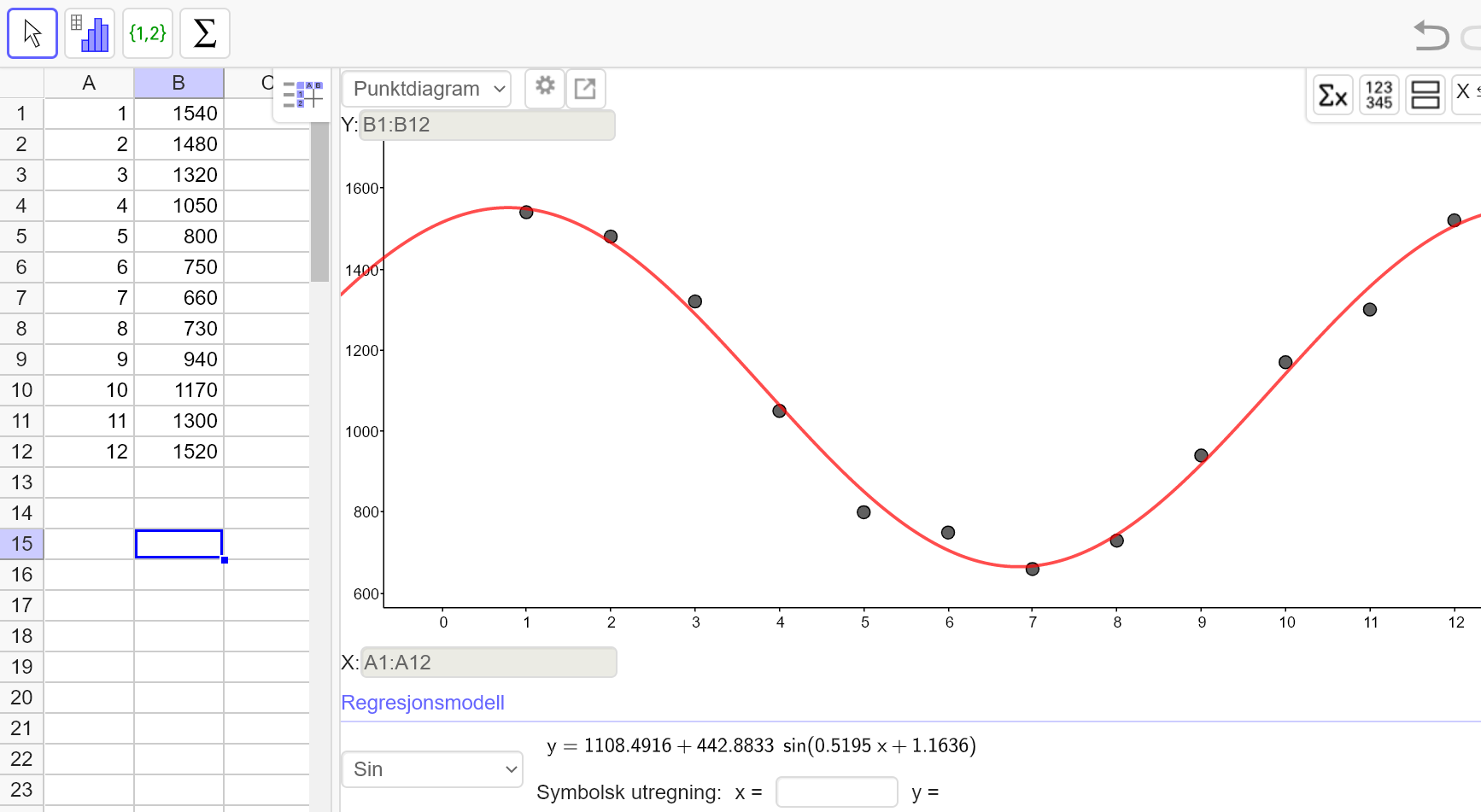
Bruker Geogebra til å utføre en regresjonsanalyse. | |||
[[File: R2_V20_del2_1a.png]] | |||
En trigonometrisk funksjon som passer godt med informasjonen i tabellen er: | |||
===b)=== | |||
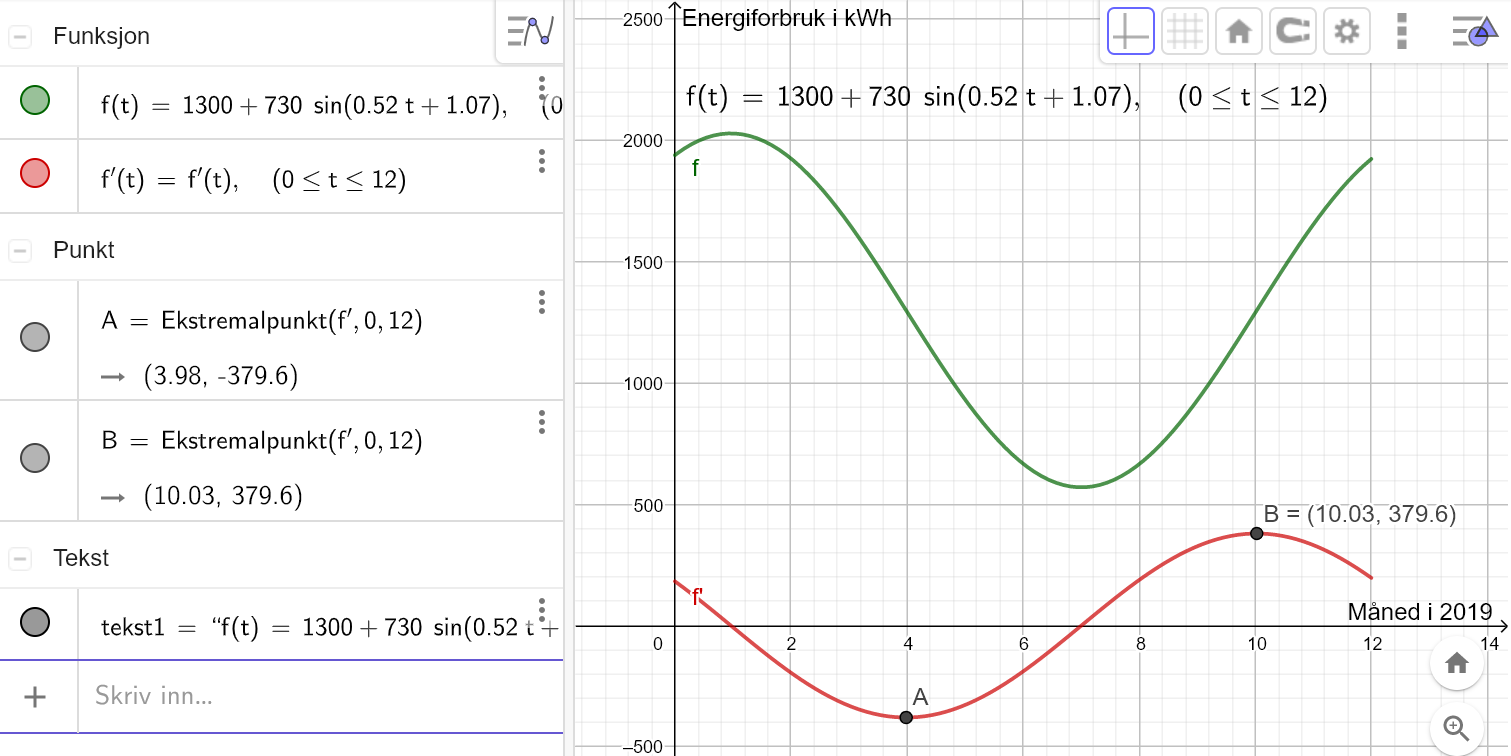
Bruker Geogebra til å tegne grafen til | |||
[[File: R2_V20_del2_1b.png]] | |||
Ifølge modellen økte forbruket raskest den 10. måneden, altså oktober. | |||
===c)=== | |||
Bruker Geogebra til å bestemme integralet. | |||
[[File: R2_V20_del2_1c.png]] | |||
===d)=== | |||
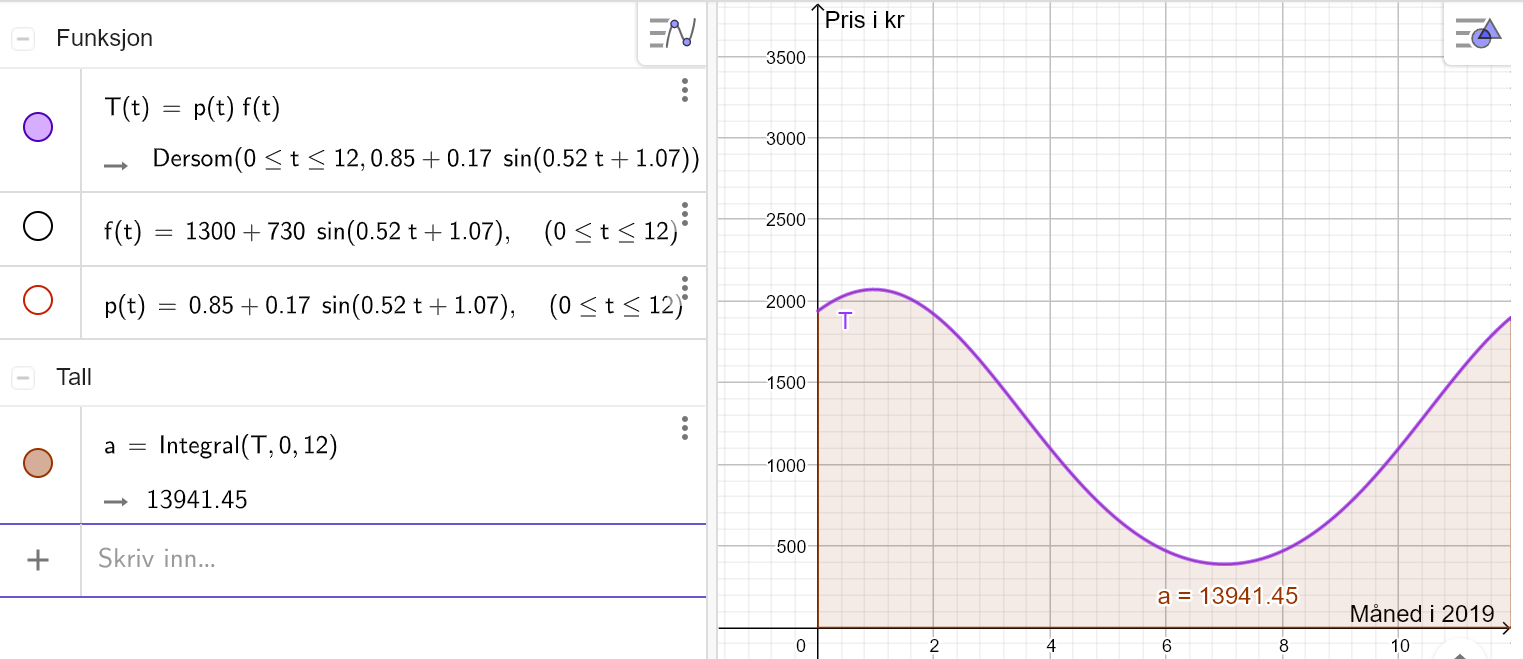
Bruker Geogebra. Funksjonen | |||
Bestemmer | |||
[[File: R2_V20_del2_1d.png]] | |||
Den årlige energikostnaden til boligen er 13941,5 kr ifølge modellen. | |||
==Oppgave 2== | |||
===a)=== | |||
Differensiallikningen | |||
<i>k</i> er proporsjonalitetskonstanten, og denne må være mindre enn null, fordi massen til det radioaktive stoffet avtar. Vekstfarten, <i>M'</i>, er altså negativ, og da må vi også ha <i>k<0</i> i differensiallikningen. | |||
===b)=== | |||
Bruker CAS i Geogebra 6.0. | |||
[[File: R2_V20_del2_2b.png]] | |||
Løser differensiallikningen i linje 1, setter inn (6,97) i linje 2 for å finne k. | |||
===c)=== | |||
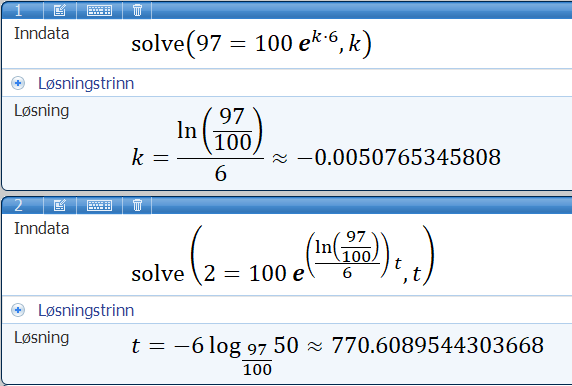
Bruker Microsoft Mathematics til å løse likningen M(t)=2, da CAS i Geogebra ikke ser ut til å fungere. | |||
[[File: R2_V20_del2_2c.png]] | |||
Det vil ta ca. 771 timer før massen til det radioaktive stoffet er 2 mg. | |||
===d)=== | |||
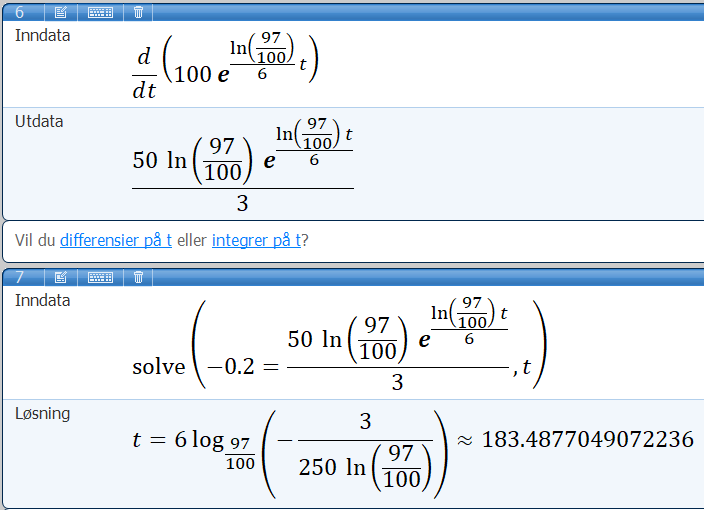
Bruker Microsoft Mathematics. Deriverer M(t) i første linje, og løser | |||
[[File: R2_V20_del2_2d.png]] | |||
Det tar ca. 183,5 timer før stoffet ikke lenger blir vurdert som helsefarlig. | |||
==Oppgave 3== | |||
===a)=== | |||
Summen av diameterne de n innerste rundene kan uttrykkes ved den aritmetiske rekken: | |||
Diameteren i runde nr. 50: | |||
Summen av diameterne de 50 innerste rundene: | |||
Summen av omkretsene (lengden på papiret) de 50 innerste rundene: | |||
Det vil være omtrent 9 meter papir igjen på tørkerullen når det er 50 runder igjen før den er tom. | |||
===b)=== | |||
Finner "rundenummer" når diameteren er 20,00 cm (bruker Microsoft Mathematics). 20,00 cm er ytre diameter av tørkerullen, så indre diameter denne runden vil være | |||
[[File: R2_V20_del2_3b.png]] | |||
Summen av omkretsene (lengden på papiret) de 500 innerste rundene: | |||
Det er omtrent 196,1 meter papir på tørkerullen når diameteren <i>D</i> er 20,00 cm. | |||
===c)=== | |||
Finner "rundenummer" når det er 500 meter papir (altså 50000 cm) igjen på tørkerullen (bruker Microsoft Mathematics): | |||
[[File: R2_V20_del2_3c.png]] | |||
Vi har rundenummer 877. | |||
Indre diameter til runde nr. 877: | |||
Ytre diameter til tørkerullen: | |||
Diameteren er omtrent 31,3 cm når det er 500 meter igjen på tørkerullen. | |||
==Oppgave 4== | |||
Vi har punktet <i>A(-1,-1,2), B(3,4,-1), C(5,3,1) og D(5,6,4)</i>. Planet | |||
Bruker CAS i Geogebra 6.0. | |||
[[File: R2_V20_del2_4.png]] | |||
Linje 5: finner likning for planet | |||
De mulige koordinatene til S er | |||
Siste sideversjon per 15. mai 2022 kl. 18:54
Diskusjon av denne oppgaven på matteprat
Løsning del 1 av Kristian Saug
Løsning del 2 av Kristian Saug
Løsning del 1 og del 2 av Lektor Trandal
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
Videoløsninger Del 1 laget av Lektor Håkon Raustøl
Videoløsninger Del 2 laget av Lektor Håkon Raustøl
Videoløsning del 1 laget av Lektor Lainz
Videoløsning del 2 av Lektor Lainz
DEL 1
Oppgave 1
a)
b)
Oppgave 2
a)
b)
Bruker variabelskifte, der
c)
Bruker delvis integrasjon, der
Finner det ubestemte integralet:
Finner det bestemte integralet:
Oppgave 3
a)
Finner
Finner differensen:
Finner
Finner summen av de 10 første leddene:
b)
Dersom
I slike tilfeller er
I rekken
Vi har
Bestemmer summen av rekken:
Oppgave 4
a)
Setter
Finner y-koordinatene til ekstremalpunktene (vet at en sinusfunksjon kun har topp- og bunnpunkter, og ingen terrassepunkter):
Toppunkter:
Bunnpunkter:
b)
Skjæring med y-aksen:
Grafen til
Skjæring med x-aksen; setter
Grafen til
c)
Bruk ekstremalpunktene og nullpunktene, samt skjæring med y-aksen, til å lage en skisse for hånd.
Oppgave 5
Vi har punktene A(-1,3,2), B(2,2,1), C(0,1,0) og T(5,3,8).
a)
b)
Volumet av pyramiden ABCT er 5.
c)
Likningen for et plan er
Der a, b og c er koordinatene til planets normalvektor, og
Vi har planets normalvektor
Vi får da likning for planet som inneholder punktene A, B og C:
Oppgave 6
En uendelig geometrisk rekke er gitt ved
a)
Vi har kvotienten
og
Rekken konvergerer når
b)
Summen av rekken er gitt ved
Summen av rekken blir 4 når
Oppgave 7
Vi har differensiallikningen
Sjekker stigningstallet til tangenten i hvert av punktene:
Punkt A(2,2):
Punkt B(-2,2):
Punkt C(-2,-2):
Punkt D(2,-2):
Den markerte tangentretningen samsvarer med retningen til tangenten til integralkurven som går gjennom punkt B og C, men ikke A og D. I punkt A viser den markerte tangentretningen stigningstall 0, og i punkt D stigningstall
Oppgave 8
Linje
Linja
Skjæringspunktet mellom linje
Finner et uttrykk for s:
Setter inn uttrykket for s i likning
Setter inn uttrykket for t i uttrykket for s fra likning
Setter inn t = -1 i parameterfremstillingen for linje
Sentrum i kula er S(3,1,2). Bestemmer radius til kula:
Radius i kula er 9. Finner likning for kuleflaten:
Oppgave 9
En følge er gitt ved
1. Induksjonsgrunnlag:
2. Induksjonstrinnet: Vi antar at
Vi har
Hvilket skulle vises.
DEL 2
Oppgave 1
a)
Bruker Geogebra til å utføre en regresjonsanalyse.
En trigonometrisk funksjon som passer godt med informasjonen i tabellen er:
b)
Bruker Geogebra til å tegne grafen til
Ifølge modellen økte forbruket raskest den 10. måneden, altså oktober.
c)
Bruker Geogebra til å bestemme integralet.
d)
Bruker Geogebra. Funksjonen
Bestemmer
Den årlige energikostnaden til boligen er 13941,5 kr ifølge modellen.
Oppgave 2
a)
Differensiallikningen
k er proporsjonalitetskonstanten, og denne må være mindre enn null, fordi massen til det radioaktive stoffet avtar. Vekstfarten, M', er altså negativ, og da må vi også ha k<0 i differensiallikningen.
b)
Bruker CAS i Geogebra 6.0.
Løser differensiallikningen i linje 1, setter inn (6,97) i linje 2 for å finne k.
c)
Bruker Microsoft Mathematics til å løse likningen M(t)=2, da CAS i Geogebra ikke ser ut til å fungere.
Det vil ta ca. 771 timer før massen til det radioaktive stoffet er 2 mg.
d)
Bruker Microsoft Mathematics. Deriverer M(t) i første linje, og løser
Det tar ca. 183,5 timer før stoffet ikke lenger blir vurdert som helsefarlig.
Oppgave 3
a)
Summen av diameterne de n innerste rundene kan uttrykkes ved den aritmetiske rekken:
Diameteren i runde nr. 50:
Summen av diameterne de 50 innerste rundene:
Summen av omkretsene (lengden på papiret) de 50 innerste rundene:
Det vil være omtrent 9 meter papir igjen på tørkerullen når det er 50 runder igjen før den er tom.
b)
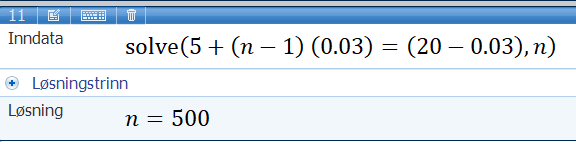
Finner "rundenummer" når diameteren er 20,00 cm (bruker Microsoft Mathematics). 20,00 cm er ytre diameter av tørkerullen, så indre diameter denne runden vil være
Summen av omkretsene (lengden på papiret) de 500 innerste rundene:
Det er omtrent 196,1 meter papir på tørkerullen når diameteren D er 20,00 cm.
c)
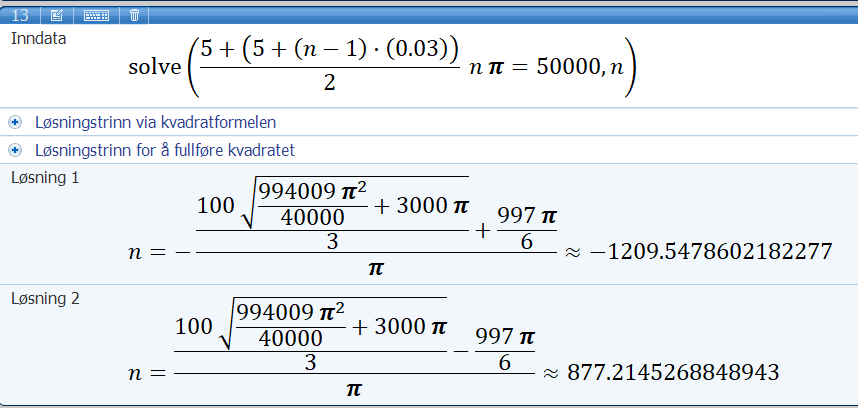
Finner "rundenummer" når det er 500 meter papir (altså 50000 cm) igjen på tørkerullen (bruker Microsoft Mathematics):
Vi har rundenummer 877.
Indre diameter til runde nr. 877:
Ytre diameter til tørkerullen:
Diameteren er omtrent 31,3 cm når det er 500 meter igjen på tørkerullen.
Oppgave 4
Vi har punktet A(-1,-1,2), B(3,4,-1), C(5,3,1) og D(5,6,4). Planet
Bruker CAS i Geogebra 6.0.
Linje 5: finner likning for planet
De mulige koordinatene til S er